之前提到过,矩阵乘法可以视作对向量基底的改变,而基底的选取可能直接导致向量维度的改变。一个2*3矩阵可以把二维向量映射到三维空间,故矩阵可以被视作操控空间的一种手段。
矩阵改变了向量维度
为弄懂这种变换的具体性质,我们必须从矩阵本身开始分析。依照之前的思路,矩阵的各列是基底向量,矩阵的右乘就是对列向量的线性组合,同理,矩阵左乘可以看作是对矩阵行向量的线性组合,所以矩阵的列构成了列空间,行构成了行空间。经线性变换后,若有T(x)=0 亦即 Ax=0, 则称 x 在A的零空间N(A)中。
我们用秩来表示矩阵空间的维度,虽然m*n矩阵的输入和输出对象是n维向量和m维向量,但列空间和行空间的秩并不一定是n和m,拿列空间举例,若矩阵的基底向量间是线性相关的,那么这组基底张开的空间维度就会下降。列秩是A的线性无关纵列的极大数目,行秩是最大数目的线性无关行
对于m*n的矩阵,线性变换T(或A)的作用范围是整个n维空间,而T(x)只能处于零空间N(A)和列空间中,更进一步,我们可以把四维空间分成两个子空间,矩阵行空间和所有与行空间垂直的空间,与行空间垂直的空间被映射为0,故它亦是零空间。剩下的所有包含于行空间内的向量,以及行空间和零空间的线性组合,都会被映射到列空间。
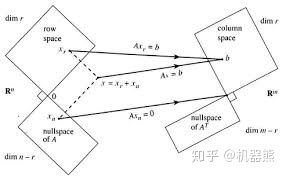
矩阵的四个子空间
秩-零度定理
在线性代数中,秩-零化度定理给出了一个线性变化或一个矩阵的秩(rank)和零化度(nullity) 之间的关系。
dim N(A)+dim rank(A)=n
矩阵零空间的维度和矩阵的秩的和就是向量所在维度n,先假设在维度n中有n个线性独立的向量基底,其中{a1,a2.....}为所有满足T(c1a1+c2a2+.....)=0的基底,{c1,c2.....}为随机系数,对剩下的向量基底{b1,b2.....}来说,T(C1b1)+T(C2b2)+.....=T(C1b1+C2b2+.....)。为证明变换前后的维度大小不变,需证明T(C1b1+C2b2+.....)!=0。
若T(C1b1+C2b2+.....)=0,则 C1b1+C2b2+.....= c1a1+c2a2+.....,因为所有基底向量线性无关,此时所有随机系数都等于0,也就是说除非C1,C2....=0,否则T(C1b1)+T(C2b2)+.....!=0,故{T(C1b1),T(C2b2)....}线性无关,且两者的线性无关基底数目之和为n,定理得证。通过证明我们也可以看到矩阵的行秩等于列秩。
行秩和列秩
行秩等于列秩是矩阵的性质之一,如果设矩阵的列秩为r,行秩为c,将矩阵中r个线性无关向量组成一个m*r的矩阵,那么m*n的矩阵就可以视作成m*r和r*n的两个矩阵的乘积(可以化成这样是因为所有的列向量都可以由这r列组合成),这时从左乘的角度来看,所有的行向量都可以视作对r*n矩阵的线性组合,故c<=r,对A的转置使用同样的操作,则有r小于等于c,所以r等于c,行秩等于列秩。同时观察到所有矩阵都可以分解成列秩向量和行秩向量的乘积。