莫比乌斯反演作用

我们规定函数 $f(n)$ 代表如下含义： $f(n)\ =\ \sum_{d|n} g(d)$ 。

在某一些情况下，莫比乌斯反演的 $f$ 函数很容易求解，但其中的g函数则不容易求解；我们需要通过某一种算法，在知道每一个 $g$ 的情况下求解出对应的 $f$ 值。

而这一个算法就是莫比乌斯反演。

莫比乌斯反演具体内容

莫比乌斯函数μ

$μ(i)= \begin{cases} 1， \text{i\ =\ 1} \\ (-1)^{k}，i=p_1*p_2*...*p_k \\ 0，i不满足上述两种限制 \end{cases}$

对于莫比乌斯函数的性质：

对于任意正整数， $\sum_{i=1}^{n} μ(i)= \begin{cases} 0，i>1 \\ 1，i=1 \end{cases}$
莫比乌斯函数是积性函数。

~~证明不想写~~

至于莫比乌斯函数的求法，由于这是一个积性函数我们可以代到线性筛了，类似于欧拉函数的求法即可。

如果没有被枚举到，说明是质数；那么这一个数的函数值是 $-1$ .
如果没有被最小质因子整除，说明仍然由若干个质数拼接而成；因此Miu值在原来的基础上乘上 $-1$ .
若不满足上述情况， $Miu$ 值为 $0$ .

代码如下：

void Find_Miu(void)
{
	int m = 0;
	Miu[1] = 1;
	for (int i=2;i<=N;++i)
	{
		if (vis[i] == 0) prime[++m] = i, Miu[i] = -1;
		for (int j=1;j<=m && i*prime[j] <=N;++j)
		{
			vis[i*prime[j]] = 1;
			if (i%prime[j] == 0) 
			{
				Miu[i*prime[j]] = 0;
				break;
			}
			Miu[i*prime[j]] = -Miu[i];
		}
	}
	return;
}

莫比乌斯反演公式

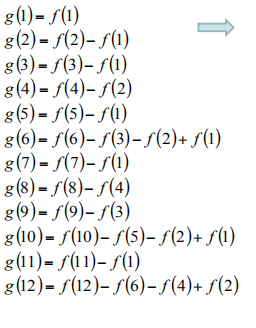
在这里插入图片描述
1.我们通过观察这一串算是，发现在计算每一份 $g$ 函数的时候，等号右边的数都是g的因数。
2.同时我们发现，对于右边的每一个数k来说，一定满足 $\lfloor\ \frac{n}{k}\ \rfloor$ 一定由若干个互不相同的质因数组成。且对应的符号为 $μ(\frac{n}{k})$ .

因此我们就可以得到莫比乌斯反演公式： $g(i)\ =\ \sum_{d|i}μ(d)*f(\frac{n}{d})$

然后就可以根据 $f$ 来求 $g$ 了。

莫比乌斯反演公式变形

~~我们不能执着于证明（九年级语文书都说了不求甚解是好的）~~

对于每一个莫比乌斯函数f(i)来说，\sum的内容是小于i的，如果所求需要大于i值、那么我们需要使用下面两个莫比乌斯反演的变形公式。

$f(i)\ =\ \sum_{d=1}^{\lfloor \frac{n}{i}\rfloor}\ g(i*d)\iff g(i)\ =\ \sum_{d=1}^{\lfloor \frac{n}{i}\rfloor}μ(d)*f(i*d)$
$f(i)\ =\ \sum_{i|d,d\leq n} g(d)\ \iff\ g(i)\ =\ \sum_{i|d,d\leq n}f(d)*μ(\frac {n}{d})$

除法分块

对于一个数n除以一个数k来说，会有若干个不同的除数，此时这一个下取整除数的序列会十分有规律的排布，我们正是需要通过除法分块来找寻这一个规律。

例如20去除以1-20的数字，我们分别得到的的序列是： $20,10,6,5,4,3,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1$

对于一开始的除数，分布并非十分规律，但是后面却会出现大量重复，我们这要找到这一个重复序列的左右端点来减少运算量。我们可以证明，这样的序列不超过 $2\sqrt n$ 个.

证明：
若 $k<\sqrt n$ 时，共有 $\sqrt n$ 个取值。
若 $k>\sqrt n$ 时，由于 $\lfloor \frac{n}{k}\rfloor<\lfloor \sqrt n \rfloor$ ，共有 $\sqrt n$ 个取值。
因此答案一定不超过 $2\sqrt n$ 个。

现在我们来尝试找到每一个相同区间的左右端点。

即对于左端点i，我们来尝试寻找右断电j。我们知道对于每一份区间，都有：
$\lfloor \frac{n}{i}\rfloor \leq \frac{n}{j}$

由于j要取最大值，因此就有 $j\ =\ \frac{i}{\lfloor \frac{n}{i}\rfloor}$ .

『数学相关』莫比乌斯反演学习笔记

文章目录