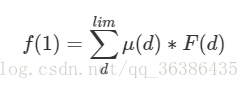莫比乌斯反演初次学习

两篇介绍的较好的博客：
莫比乌斯反演入门：https://blog.csdn.net/hzj1054689699/article/details/51659994
初涉莫比乌斯反演：https://blog.csdn.net/litble/article/details/72804050

例题：
hdu1695
GCD
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 15939 Accepted Submission(s): 6132

Problem Description
Given 5 integers: a, b, c, d, k, you’re to find x in a…b, y in c…d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you’re only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.

Yoiu can assume that a = c = 1 in all test cases.

Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.

Output
For each test case, print the number of choices. Use the format in the example.

Sample Input
2
1 3 1 5 1
1 11014 1 14409 9

Sample Output
Case 1: 9
Case 2: 736427

Hint
For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).

题解详细解释：https://blog.csdn.net/wubaizhe/article/details/73741901

求对于区间[1，b]内的整数x和[1,d]内的y，满足gcd(x,y)=k的数对的个数。
只要让F（t）=满足gcd(x,y)%t==0的数对个数
f(t)=满足gcd(x,y)=t的数对个数，则F（t）和f(t)就存在莫比乌斯反演的关系了。显然F（t）=(b/t)*(d/t)
因为如果gcd(x,y)=1,则gcd(x∗k,y∗k)=k，所以我们把b和d同时除以k，得到的f(1)再去重就是答案。令lim=min(b/k,d/k),而根据上面的莫比乌斯反演第二个公式，

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 5;

int prime[N];
int mu[N];
int vis[N];
void getprime(int n)
{
    memset(vis,false,sizeof(vis));
    int num = 0;
    for(int i = 2;i <= n;++i)
    {
        if(!vis[i]){
            prime[num++] = i;
            //本身就是质因子，所以是莫比乌斯函数值是-1
            mu[i] = -1;
        }
        for(int j = 0;i * prime[j] <= n;++j)
        {
            vis[i * prime[j]] = true;
            //如果不写这个，会进行重复计算，
            if(prime[j] == i) break;
            if(!(i % prime[j]))
            {
                //i存在质因子存在多个
                mu[i * prime[j]] = 0;
                break;
            }
            mu[i * prime[j]] = -1 * mu[i];
        }
    }
}

int main()
{
    mu[1] = 1;
    getprime(100005);
    int t;
    scanf("%d",&t);
    int tt = 0;
    while(t--)
    {
        tt++;
        int a,b,c,d,k;
        scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
        if(k == 0 || k > b || k > d){
            printf("Case %d: 0\n",tt);
            continue;
        }
        int n = b / k;
        int m = d / k;
        LL ans1 = 0;
        LL ans2 = 0;
        //cout << n << " " << m << endl;
        if(n > m){
            swap(n,m);
        }
        for(int i = 1;i <= n;++i)
            ans1 += (LL)mu[i] * (n / i) * (m / i);
        for(int i = 1;i <= n;++i)
            ans2 += (LL)mu[i] * (n / i) * (n / i);
        printf("Case %d: %lld\n",tt,ans1 - ans2 / 2);
    }
    return 0;
}