清华大学公开课线性代数2——第6讲：伪逆

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/you1314520me/article/details/78857759

此博客停止更新，迁移至SnailDove’s blog，查看本文请点击此处，清华大学线性代数2笔记汇总：线性代数总结

笔记源自：清华大学公开课：线性代数2——第6讲：伪逆

**提示：**如果文中图片看不清文字，请右键单击鼠标，选择在新窗口打开图片，然后放大图片（这边上传之前都是可以看清的，由于网页正文部分大小固定，因此图片被自动缩小以便适配网页），截图部分是课堂ppt老师随手的板书。

引言

本文基础：SVD分解原理

矩阵的奇异值分解可以理解成从 $R^n$到 $R^m$的线性变换在不同基底下矩阵表示，接下来利用矩阵的奇异值分解
来定义矩阵的伪逆，然后再利用矩阵的伪逆来讨论线性方程组Ax＝b无解时的最小二乘解，线性代数的中心问题是
求解线性方程组 $Ax=b$，最简单的情况是如果系数矩阵A是n阶的可逆矩阵，那么这时对于任意的n维向量 $b$，线性方程组 $Ax=b$有唯一的解，这个解是 $A^{-1} b$，那这就启发去对于不可逆的矩阵或者是对于 $A_{m\times n}$的矩阵，我们来定义它的一个逆矩阵，那么这时候逆矩阵我们叫做伪逆或者是叫广义逆 。

##定义

伪逆的定义来自于奇异值分解：

(1)若 $A$可逆，即 $r=m=n$，则： $A^{-1}=(U\Sigma V^T)^{-1}=V\Sigma^{-1}U^T=A^+$，注意：由奇异值分解公式 $AV=U\Sigma,\ (v_1\,...\,v_r)\in C(A^T),\ (v_{r+1}\,...\,v_n)\in N(A),\ (u_1\,...\,u_r)\in C(A),\ (u_{r+1}\,...\,u_m)\in N(A^T)$ 得： $AV=U\Sigma: C(A^T)\rightarrow C(A)$，同理可得： $A^+U^T=V\Sigma^{+}:C(A)\rightarrow C(A^T)$

(2) $AA^+=(U\Sigma_{m\times n} V^T)(V\Sigma^+_{n\times m}U^T)=U\Sigma_{m\times n}\Sigma^+_{n\times m}U^T=U\begin{pmatrix}I_r&0\\0&0\end{pmatrix}_{m\times m}U^T$ 得出以下3个性质：

• 对称性： $(AA^+)^T=AA^+$
• $AA^+=u_1u_1^T+\,...\,+u_ru_r^T, U=(u_1,\,...\,u_r,\,u_{r+1}\,...\,,u_n)$
• $AA^+=R^m$到 $C(A)$的正交投影矩阵， $AA^+|_{C(A)}=id, AA^+|_{N(A^T)}=0$
  • 证明1： $AA^+x=(u_1u_1^T+\,...\,+u_ru_r^T)x=(u_1^Tx)u_1+\,...\,+(u_r^Tx)u_r$，由奇异值svd分解得到 $V=(v_1,\,...\,,v_r)$是 $A^T$列空间（即 $C(A^T)$）的单位正交特征向量基，而 $U=(u_1,\,...\,,u_r)$是 $C(A)$的单位正交特征向量基，所以 $AA^+$是投影到 $C(A)$的正交投影矩阵（即保留了 $C(A)$的部分），因此 $AA^+$限制在 $C(A)$的变换即变成了恒等变换。而 $U$中 $(u_{r+1}\,...\,u_m)$和 $U^T$中 $(u_{r+1}\,...\,u_m)^T$即属于 $N(A^T)$的基乘以矩阵 $\begin{pmatrix}I_r&0\\0&0\end{pmatrix}_{m\times m}$中右下角的 $0$相当于对属于 $N(A^T)$的部分做了零变换。
  • 证明2： $A^+u_j={1\over \sigma_j}v_j\Rightarrow AA^+u_j=A({1\over\sigma_j}v_j)={1\over \sigma_j}Av_j$ 再根据奇异值分解中 $Av_j=\sigma u_j, (1\le j \le r)$ 得 $AA^+u_j=u_j(1\le j\le r),\ AA^+u_j=0(r+1\le j \le m)$
  • 验证： $(AA^+)(AA^+)=U\begin{pmatrix}I_r&0\\0&0\end{pmatrix}_{m\times m}U^TU\begin{pmatrix}I_r&0\\0&0\end{pmatrix}_{m\times m}U^T$，由于从svd分解知道 $U$是单位正交特征向量基 ，因此： $U^T=U^{-1}\Rightarrow (AA^+)(AA^+)=U\begin{pmatrix}I_r&0\\0&0\end{pmatrix}_{m\times m}U^T=AA^+$，这正是投影的性质：多次投影结果还是第一次投影结果。
  • 结果： $\forall\ p\in R^m, b=p+e, p\in C(A), e\in N(A^T), AA^+b=p$

(3) $A^+A=(V\Sigma^+_{n\times m}U^T)(U\Sigma_{m\times n} V^T)=V\begin{pmatrix}I_r&0\\0&0\end{pmatrix}_{n\times n}V^T$ 得到以下三个性质（证明同上）：

• $(A^+A)^T=A^+A$
• $A^+A=v_1v_1^T+\,...\,+v_rv_r^T$
• $A^+A=R^n$到 $C(A^T)$的正交投影矩阵（ $A^+A|_{C(A^T)}=id,\quad A^+A|_{N(A)}=0$）:
  • $\forall\ x\in R^n=C(A^T)\bigoplus N(A)),\ x=x_{1,r}+x_{r+1,n}, \ x_{1,r}\in C(A^T),\ x_{r+1,n}\in N(A^T),\\ A^+Ax=A^+A(x_1,\,...\,x_r,x_{r+1},\,...\,x_n)=x_{1,r}$

为什么称为伪逆、左逆、右逆

##例子

注： $u_1, u_2,u_3$ 是 $R^m$的一组基底那么它是 ${Av_1\over \sigma_1}$，那么很容易计算出来，是 ${1\over\sqrt{2}}\begin{pmatrix}1\\1\\0\end{pmatrix}$那 $u_2$和 $u_3$ 分别是0所对应的特征向量， $u_2$和 $u_3$可以看成是三维空间里头， $u_1$的正交补所给出来的单位正交的向量。

特例

Jordan标准形的伪逆

推导结论： $J_n^+=J_n^T$，Jordan标准形的伪逆是它自己的转置。
##Moore-Penrose伪逆
###E.H.Moore伪逆

Penrose伪逆

注：

1. A可以是mxn的复数矩阵，这样的话(3)(4)里面就变成共轭转置。
2. Penrose伪逆与E.H.Moore伪逆定义是等价的。

$(1)AXA =A \Rightarrow AXAX=AX\Rightarrow (AX)^N=AX\Rightarrow AX$ 是幂等矩阵，投影矩阵
$(2)XAX=X\Rightarrow XAXA=XA\Rightarrow (XA)^N=XA\Rightarrow XA$ 是幂等矩阵，投影矩阵
$(3)(AX)^T=AX\Rightarrow AX$ 是对称矩阵
$(4)(XA)^T=XA\Rightarrow XA$ 是对称矩阵

通过奇异值分解得到的伪逆矩阵 $A^+$， $AA^+: R^m \rightarrow C(A)$， $A^+A:R^n\rightarrow C(A^T)=C(A^+)$，前文已经证明两者都是对称的，所以符合Penrose对伪逆矩阵的定义。对于伪逆唯一性的证明上文图片太小可以放大来看。

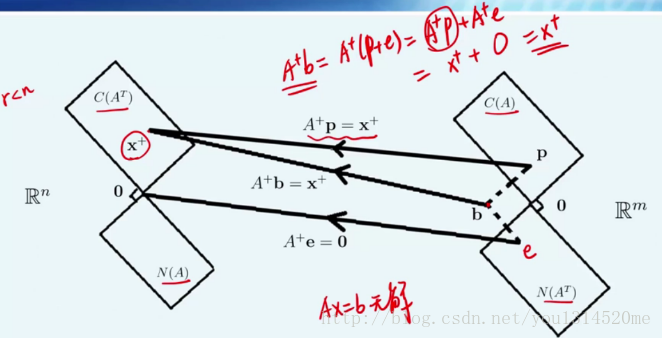
伪逆的应用之最小二乘法

引言

**但是我们需要求 $e$ 即误差最小的解！**但是这时候 $A_{m\times n}$不是列满秩不存在逆矩阵，于是自然地想到利用伪逆求解。
###伪逆求解正规方程——最佳最小二乘解

注：由于 $A^+$ 来自于： $A^+U^T=V\Sigma^{+},\ (v_1\,...\,v_r)\in C(A^T),\ (v_{r+1}\,...\,v_n)\in N(A),\ (u_1\,...\,u_r)\in C(A),\ (u_{r+1}\,...\,u_m)\in N(A^T),\\\Sigma^+=\begin{pmatrix}{1\over \sigma_1}\\&{1\over \sigma_2}\\&&.\\&&&.\\&&&&{1\over \sigma_r}\\&&&&&0\end{pmatrix}_{n\times m}\Rightarrow A^+: C(A)\rightarrow C(A^T)$，另外由于 $A^TAx=0, Ax=0$ 同解所以零空间相同。

最佳最小二乘解的四个基本子空间