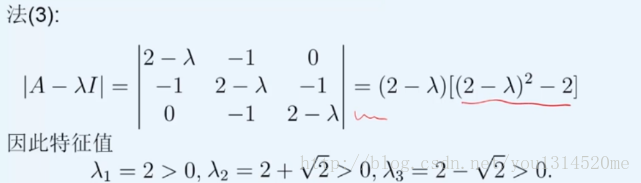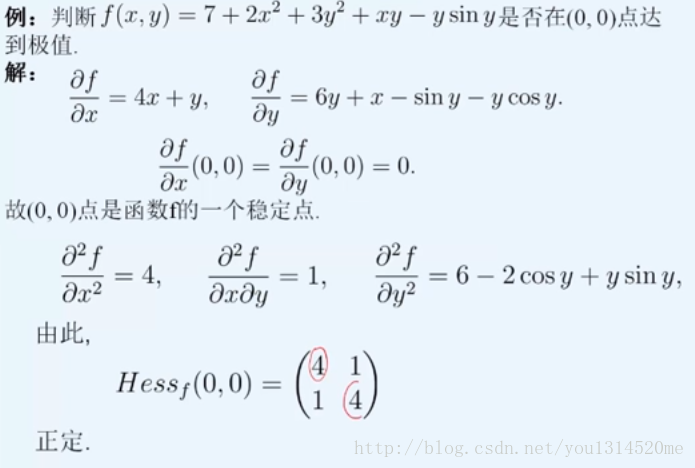清华大学公开课线性代数2——第1讲：正定矩阵

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/you1314520me/article/details/78856322

此博客停止更新迁移至SnailDove’s Blog，查看本文点击 此处 清华大学线性代数2笔记汇总：线性代数总结
笔记源自：清华大学公开课：线性代数2——第1讲：正定矩阵，涉及：正定矩阵、二次型、合同、惯性定理、Hessian

**提示：**如果文中图片看不清文字，请右键单击鼠标，选择在新窗口打开图片，然后放大图片（这边上传之前都是可以看清的，由于网页正文部分大小固定，因此图片被自动缩小以便适配网页），截图部分是课堂ppt老师随手的板书。

引言

矩阵特征值的正负在求解微分方程和差分方程时，会影响解是否收敛，例如上图如果 $\lambda_i < 0$那么 $e^{\lambda_i t}$ 随着 $t\rightarrow \infty, e^{\lambda_it}\rightarrow0$

主子式

实对称矩阵A正定的充要条件

下列6项条件，满足任意一项即可判定实对称矩阵 $A$为正定矩阵：

###证明

$(1)\Rightarrow(2):$ 对实对称矩阵 $A$，那么存在正交阵 $Q$，使得 $AQ=Q\Lambda \rightarrow A=Q\Lambda Q^T$，其中 $\Lambda=diag(\lambda_1,\,...\,,\lambda_n)$。于是对于任意非零向量 $x$，有 $x^TAx=x^TQ\Lambda Q^Tx=y^T \Lambda y=\lambda_1 {y_1}^2+\,...\,+\lambda_n {y_n}^2>0, y=Q^Tx=(y_1,\,...\,,y_n) \ne\vec{0}$

$(2)\Rightarrow(1):$ 设 $Ax=\lambda x(x\ne0)$ 则 $0<x^TAx=x^T\lambda x=\lambda||x||^2$，因此所有 $\lambda_i>0$。

$(2)\Rightarrow(3):$ 由于行列式等于矩阵特征值的乘积，故 $(2)\Rightarrow(1)\Rightarrow (3)det A=\lambda_1\,...\,\lambda_n>0$ ：

$(2)\, 0<\begin{pmatrix}x_k^T&0\end{pmatrix} \begin{pmatrix}A_k&*\\*&*\end{pmatrix}\begin{pmatrix}x_k\\0\end{pmatrix}={x_k}^T A_k x_k = {x_k}^T \begin{pmatrix} \lambda_1&\\&.\\&&. \\&&&. \\ &&&&\lambda_k \end{pmatrix} x,\, (1 \le k \le n) \\\Rightarrow (1) \lambda_i > 0,(1\le i \le k, 1 \le k \le n) \Rightarrow (3) detA_k>0, (1 \le k \le n)$

$(3)\Rightarrow(4)$：顺序主子式与主元有直接联系，因为第k个主元 $d_k={det A_k \over det A_{k-1}}$，所以 $(3) \Rightarrow (4)\,d_k > 0$，其中 $A_k$是第 $k$个顺序主子矩阵（the k-th leading principal sub-matrix）。

$(4) \Rightarrow (2)$：由对称矩阵的Gauss消元法得 $A=LDL^T$且对角阵 $D=diag(d_1,\,...\,d_n)$ 的对角元为A的主元， $L$是下三角矩阵， $L^T$ 是上三角矩阵，而且根据分解结果知道 $L$的主对角线上全元素为1，也即 $L^T$的主元全为1，即 $L^T$行列式为1且是方阵，那么这俩都可逆。因为 $(4):d_1,\,...\,,d_n$大于0，那么到： $x\ne 0\Rightarrow y=L^Tx\ne 0\Rightarrow x^TAx=x^TLDL^Tx=y^TDy=d_1y_1^2+...+d_ny_n^2>0$ 。

可逆矩阵齐次方程只有零解

$(2)\Rightarrow(5)$： $A=LDL^T=L\sqrt{D}\sqrt{D}L^T=(\sqrt{D}L^T)^T(\sqrt{D}L^T)$，此时可取 $R=\sqrt{D}L^T$，因为 $\sqrt{D}, L^T$ 都可逆且都是方阵，由于 $(2)\Rightarrow(3)\Rightarrow(4)$ ，因此 $\sqrt{D}>0$，且有上面推导得 $|L^T|>0$， 可逆矩阵乘积还是可逆。

根据行列式性质：$ |A||B|=|AB| $, 当$A,B$ 均可逆，那么 $|A|>0, |B|>0 \rightarrow |AB|>0$, 所以 $AB$也可逆。

或者： $A=Q\Lambda Q^T=Q\sqrt{\Lambda}\sqrt{\Lambda}Q^T=(\sqrt{\Lambda}Q^T)(\sqrt{\Lambda}Q^T)$，此时可取 $R=\sqrt{\Lambda}Q^T$ ，同理可得。

$(5)\Rightarrow(2)$： $A=R^TR\Rightarrow x^TAx=x^TR^TRx=(Rx)^TRx=||Rx||^2 \ge 0$且 $R$是列满秩，除了 $x=0$之外，其余 $x^TAx=||Rx||^2 > 0$，即 $(5)\Rightarrow(2)$

$(6)\Leftarrow\Rightarrow(2)$:

####典型例子

正定矩阵的性质

###如果 $A,B$是正定矩阵，那么 $A+B$也是正定矩阵

###如果 $A$为正定矩阵，则存在矩阵 $C$，满足 $A=C^2$

###如果 $A$为正定矩阵，则矩阵 $A$的幂也是正定的

###如果 $A$为正定矩阵，矩阵 $C$，那么 $B=C^TAC$也是正定的

注：其实B称为A的合同矩阵

半正定矩阵的判别条件

##二次型

###定义

注意：这里证明里面 ${A-A^T\over 2}$ 是反对称矩阵，利用反对称矩阵性质，所以 $x^T{A-A^T\over 2}x=0$ 。二次型与判定正定矩阵的第二条准则密切相关。

###例子

对角形

####二次型化成对角形

注：由于实对称矩阵 $A$可以与二次型一一对应，因此，可以借助实对称矩阵研究二次型。

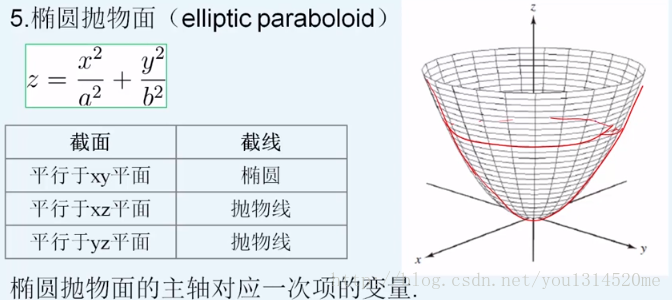
###主轴定理principal axis theorem

有心二次型central_conic

三维空间中的二次曲面-6类基本的二次曲面

$R^3$种的二次曲面的方程形如:
$a_{11}x^2+a_{22}y^2+a_{33}z^2+2a_{12}xy+2a_{13}xz+2a_{23}yz+b_{1}x+b_{2}y+b_{3}z+c=0$.

注：由于二次型可以与实对称对称矩阵一一对应，二次型里面又包括二次曲面，所以实对称矩阵可以跟二次曲面对应起来。

二次型的分类

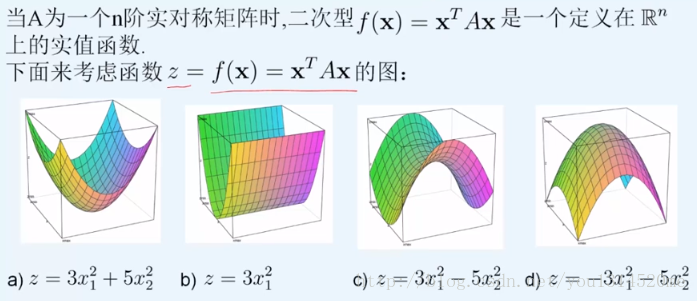
###二次型与特征值

二次型的一个应用——求二次型的几何形状

把二次型的部分去化成对角形的标准型，相应的这个一次项也作了变换，于是再做配方然后去跟基本的形状做比较得出这个曲面的几何形状，这是二次型的一个应用。

合同congruent

####前言

注：非退化矩阵即满秩矩阵

定义

例子

主轴定理与合同

####合同的性质

证明:
矩阵 $A$左乘可逆矩阵 $C^T$相当于做初等行变换，右乘以可逆矩阵 $C$相当于做初等列变换，因此根据消元法知道并不改变矩阵 $A$的秩。对称性保持证明在于二次型定义可以看到。

1.利用初等变换不改变矩阵的秩，因为可逆矩阵可以表示为初等矩阵的乘积，而A乘初等矩阵相当于对A作初等变换，所以A的秩不变-。这个方法包括了可逆矩阵左乘A，右乘A，或是左右同时乘A
2.利用 r(AB)

###惯性定理Sylvester’s law of inertia的证明

###惯性定理的应用

###正负定矩阵在函数极值中的应用

以二元函数 $f(x,y)$为例：设 $(x_0,y_0)$是二元函数 $f(x,y)$的一个稳定点，即： $\frac{\partial f}{\partial x}(x_0,y_0)={\partial{f}\over \partial{y}}(x_0,y_0)=0$。如果 $f(x,y)$在 $(x_0,y_0)$的领域里有三阶偏导数，则 $f(x,y)$在 $(x_0,y_0)$可展开成Talor级数：

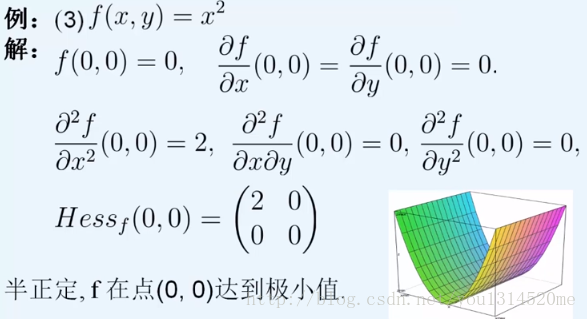
####黑塞Hessian矩阵

黑塞矩阵（Hessian Matrix），又译作海森矩阵、海瑟矩阵、海塞矩阵等，是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出，并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题，利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中，所列的目标函数往往很复杂，为了使问题简化，常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数，此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。