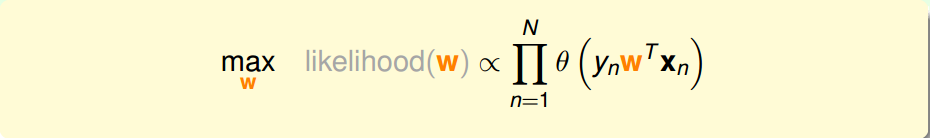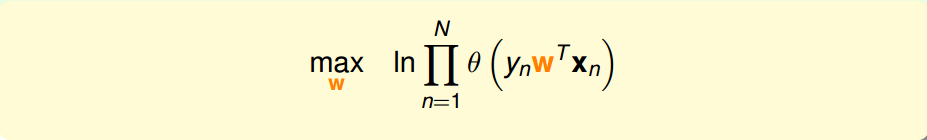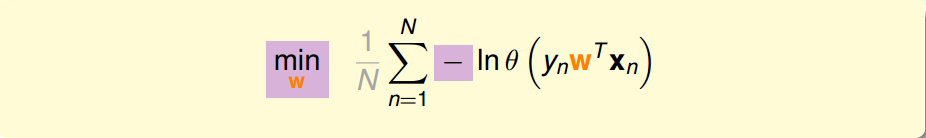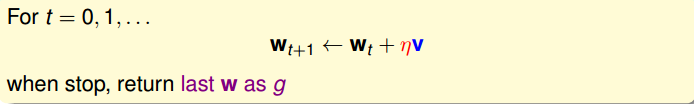Coursera机器学习基石笔记week10

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qq_35564813/article/details/84394684

Logistic Regression

Logistic Regression Problem

之前提过的二元分类器如PLA，其目标函数为， $f(x)=sign(w^Tx)∈{−1,+1}$，输出要么是-1要么是+1，是一个“硬”的分类器。而Logistic Regression是一个“软”的分类器，它的输出是y=+1的概率，因此Logistic Regression的目标函数是 $f(x)=P(+1|x)∈[0,1]$。

Logistic Regression use: $h(x)=\frac{1}{1+exp(-w^Tx)}∈[0,1]$ 来逼近它的目标函数。

Logistic Regression Error

之前我们讲到Linear Regression所使用的平方误差，那么Logistic可以使用平方误差吗？当然可以，但是使用平方误差不够好。

如果使用平方误差，每个点产生的误差是：

$
err(h,x_n,y_n) =
\begin{cases}
(\theta(w^Tx)-(0))2, & y_n=0\
(1-\theta(w^Tx))2, & y_n=1
\end{cases}\
$

​ $=y_n(1-\theta(w^Tx))^2+(1-y_n)(\theta(w^Tx))^2$

此时cost function， $E_{in}(w)=\sum err$就是一个关于w的非凸函数（non-convex）：

非凸函数由于存在很多个局部最小点，因此很难去做最优化。所以我们不使用平方误差来定义error，而是使用极大似然法来估计模型的参数。那么我们就要先来了解一下这个似然性（likelihood）。
先介绍一下“似然性”的概念。目标函数 $f(x)=P(+1|x)​$，如果我们找到了hypothesis很接近target function。也就是说，在所有的Hypothesis集合中找到一个hypothesis与target function最接近，能产生同样的数据集D，包含y输出label，则称这个hypothesis是最大似然likelihood。

Logistic Regression的目标函数的输出是，在已知x的条件下，y=+1的概率，因此在已知x的条件下，y=+1的概率是f(x)，y=−1的概率是1−f(x):

$
f(x)=P(+1|x)\Leftrightarrow P(y|x)=
\begin{cases}
f(x), &for\ y=+1\
1-f(x) &for\ y=-1
\end{cases}
$

则理想的hypothesis就是能使得似然函数最大的那个h：

​ $g=argmax_h \ likehood(h)$

当h是logistic函数的时候，即 $h(x)=θ(w^Tx)$，由于logistic函数的中心对称性，有: 1−h(x)=h(−x)

所以：

$
\begin{align}
likelihood(h)&=P(x_1)h(x_1) X P(x_2)(1-h(x_2))X…XP(x_N)(1-h(x_N))\
&=P(x_1)h(x_1) X P(x_2)(h(-x_2))X…XP(x_N)(h(-x_N))\
&=P(x_1)h(x_1) X P(x_2)(h(y_2x_2))X…XP(x_N)(h(y_Nx_N))
\end{align}
$

因为 $P(x_n)$对所有的n来说是一样的，所以我们可以忽略它。那么我们可以得到logistic h正比于所有的 $h(y_n)$乘积。我们的目标就是让乘积值最大化。

如果将w带入的话：

为了把连乘转换为连加：

然后为了找到最优的解，我们把最大值问题转换为最小值问题：

将logistic function的表达式带入，那么最小化问题就可以转化为如下形式：

我们把逻辑回归的误差函数称之为交叉熵误差：

Gradient of Logistic Regression Error

有了误差函数后，我们就可以定出cost function：

$E_{in}(w)=\frac{1}{N}\sum^N_{n=1}ln(1+exp(-y_nw^Tx_n))$

该函数是连续，可微，并且是凸函数

既然是凸函数，我们可以根据之前线性回归的例子，如果我们能解出一阶微分（梯度）为0的点，这个问题就可以解决了。

再把偏微分方程中的 $x_{n,i}$换成向量的形式，就得到了 $E_{in}(w)$的一阶微分：

$\nabla E_{in}(w)=\frac{1}{N}\sum^N_{n=1}\theta(−y_nw^Tx_n)(−y_nx_n)$

和之前的线性回归不同，它不是一个线性的式子，要让 $\nabla E_{in}(w)=0$这个式子，是困难的，那么我们应该如何使之最小化呢？

要让 $\theta()$=0的话，只有 $y_nw^Tx_n\gg0$才行。也就说对于所有的点， $y_n$与 $w^Tx_n$都是同号的，这表示数据集D必须是全部线性可分的才能成立。

但是相对来说，保证所有的权重 $\theta(-y_nw^Tx_n)$为0是不太现实的，总有不等于0的时候，那么另一种常见的情况是非线性可分，只能通过使加权和为0，来求解w。这种情况是没有closed-form解，与Linear Regression不同，只能用迭代方法求解。

我们尝试从PLA中找到些许灵感：

w每次更新包含两个内容：一个是每次更新的方向 $y_nx_n$，用v表示，另一个是每次更新的步长η。参数(v,η)和终止条件决定了我们的迭代优化算法。

Gradient Descent

根据上一小节PLA的思想，那么：

我们把 $E_{in}(w)$曲线看做是一个山谷的话，要求 $E_{in}(w)$最小，即可比作下山的过程。整个下山过程由两个因素影响：一个是下山的单位方向v；另外一个是下山的步长η。

利用微分思想和线性近似，假设每次下山我们只前进一小步，即η很小，那么根据泰勒Taylor一阶展开，可以得到：

​ $E_{in}(w_t+\eta v)\simeq E_{in}(w_t)+\eta v^T\nabla E_{in}(w_t)$

至于泰勒展开（矩阵形式）：

$f(x)=f(x_k)+[\nabla f(x_k)]^T(x-x_k)+\frac{1}{2!}[x-x_k]^TH(x_k)[x-x_k]+o^n$

迭代的目的就是让 $E_{in}$越来越小，即让 $E_{in}(w_t+\eta v)<E_{in}(w_t)$。 $\eta$是标量，因为如果两个向量方向相反的话，那么它们的内积最小（为负），也就是说如果方向v与 $\nabla E_{in}(w_t)$反向的话，那么就能保证每次迭代 $E_{in}(w_t+\eta v)<E_{in}(w_t)$都成立，那么我们让 $v=\frac{\nabla E_{in}(w_t)}{||\nabla E_{in}(w_t)||}$.

那么每次迭代的公式就可以写出： $w_{t+1}\leftarrow w_t-\eta\frac{\nabla E_{in}(w_t)}{||\nabla E_{in}(w_t)||}$

步长η比较难决定，太小了，更新太慢，太大了，容易矫枉过正:

一个比较好的做法是让 $\eta$与 $||\nabla E_{in}(w_t)||$成一定的比例，让新的和 $||\nabla E_{in}(w_t)||$成比例的 $\eta'$来代替：

$w_{t+1}\leftarrow w_t-\eta\frac{\nabla E_{in}(w_t)}{||\nabla E_{in}(w_t)||}$
​ $\Vert$

$w_t-\eta' \nabla E_{in}(w_t)$

我们称这个 $\eta'$为fixed learning rate。

整个步骤是这样的：

initialize w0

for t=0,1,…

1.compute

​ $\nabla E_{in}(w)=\frac{1}{N}\sum_{n=1}^N\theta(-y_nw^Tx_n)(-y_nx_n)$

2.update by

​ $w_t-\eta\nabla E_{in}(w_t)$

…until $E_{in}(w_{t+1})=0$ or enough iterations

return last $w_{t+1}$ as g.

总结

今天介绍了逻辑回归。首先指出逻辑回归将P(+1|x)作为目标函数，将 $\theta(w^Tx)$作业hypothesis。接着，我们定义了逻辑回归的误差函数，称之为cross-entropy error交叉熵误差。然后，我们计算逻辑回归损失函数的梯度，最后通过梯度下降算法，来逼近最小的 $E_{in}$。