Coursera机器学习基石笔记week6

Theory of Generalization

Restriction of Break Point

在这里插入图片描述
很明显，当N=1时， $m_H(N)$ =2,；当N=2时，由break point为2可知，任意两点都不能被shattered（shatter的意思是对N个点，能够分解为 $2^N$ 种dichotomies）； $m_H(N)$ 最大值只能是3；当N=3时，简单绘图分析可得其 $m_H(N)=4$ ，即最多只有4种dichotomies。

所以，我们发现当N>k时，break point限制了 $m_H(N)$ 值的大小，也就是说影响成长函数 $m_H(N)$ 的因素主要有两个：

抽样数据集N
break point k（这个变量确定了假设的类型）

那么，如果给定N和k，能够证明其 $m_H(N)$ 的最大值的上界是多项式的，则根据霍夫丁不等式，就能用 $m_H(N$ )代替M，得到机器学习是可行的。所以，证明 $m_H(N)$ 的上界是poly(N)，是我们的目标。

Bounding Function:Basic Cases

在这里插入图片描述

当k=1时，B(N,1)恒为1。
当N < k时，根据break point的定义，很容易得到 $B(N,k)=2^N$ 。
当N = k时，此时N是第一次出现不能被shatter的值，所以最多只能有 $2^N-1$ 个dichotomies，则B(N,k)= $2^N-1$ 。

Bounding Function：Inductive Cases

以B(4,3)为例，首先想着能否构建B(4,3)与B(3,x)之间的关系。

首先，把B(4,3)所有情况写下来，共有11组。也就是说再加一种dichotomy，任意三点都能被shattered，11是极限。
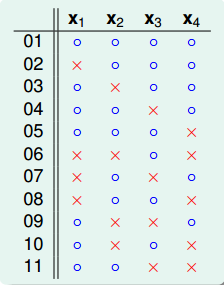
在这里插入图片描述
对这11种dichotomy分组，目前分成两组，分别是orange和purple，orange的特点是，x1,x2和x3是一致的，x4不同并成对，例如1和5，2和8等，purple则是单一的，x1,x2,x3都不同，如6,7,9三组。

然后根据分组，对橙色部分分为2 $\alpha$ ，紫色部分分为 $\beta$ ，那么 $B(4,3)=2\alpha+\beta$ 。然后我们将x4去掉，同时将橙色重复部分去除，即得 $\alpha+\beta$ 。已知任意3个点在上述11个分组中不能shatter，那么对于我们经过删减的 $\alpha+\beta$ 来说，它们也不能shatter。也就说明了 $\alpha+\beta\leq B(3,3)$ .
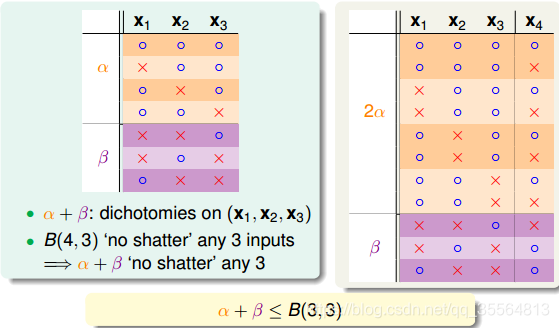
在这里插入图片描述
另一方面，由于 $\alphaα$ 中x4是成对存在的，且 $\alpha$ 是不能被任意三点shatter的，则能推导出 $\alpha$ 是不能被任意两点shatter的。这是因为，如果 $\alpha$ 是能被任意两点shatter，而x4又是成对存在的，那么x1、x2、x3、x4组成的 $\alpha$ 必然能被三个点shatter。这就违背了条件的设定。这个地方的推导非常巧妙，也解释了为什么会这样分组。此处得到的结论是 $\alpha \leq B(3,2)$
在这里插入图片描述
由此得出B(4,3)与B(3,x)的关系为：

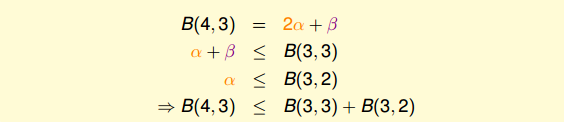
最后，推导出一般公式为：

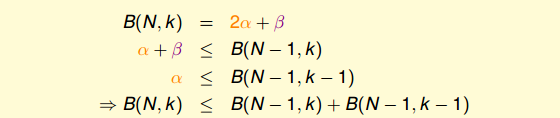
根据推导公式，下表给出B(N,K)值

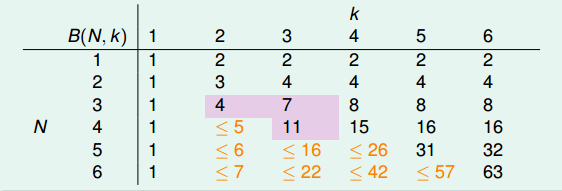
根据递推公式，推导出B(N,K)满足下列不等式：

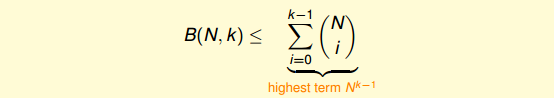
上述不等式的右边是最高阶为k-1的N多项式，也就是说成长函数 $m_H(N)$ 的上界B(N,K)的上界满足多项式分布poly(N)，这就是我们想要得到的结果。

得到了 $m_H(N)$ 的上界B(N,K)的上界满足多项式分布poly(N)后，我们回过头来看看之前介绍的几种类型它们的 $m_H(N)$ 与break point的关系：
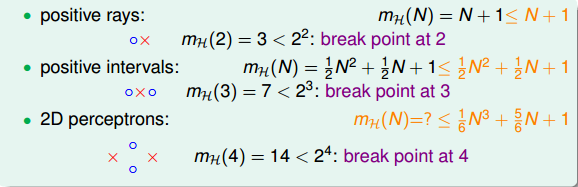
在这里插入图片描述
我们得到的结论是，对于2D perceptrons，break point为k=4， $m_H(N)$ 的上界是 $N^{k-1}$ 。推广一下，也就是说，如果能找到一个模型的break point，且是有限大的，那么就能推断出其成长函数 $m_H(N)$ 有界。

A Pictorial Proof

我们已经知道了成长函数的上界是poly(N)的，下一步，如果能将 $m_H(N)$ 代替M，代入到Hoffding不等式中，就能得到 $E_{out}\approx E_{in}$ 的结论：
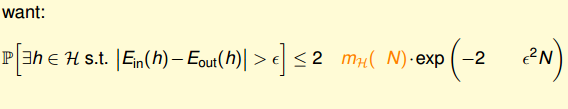
在这里插入图片描述
但是实际的表达式并不是这样的：

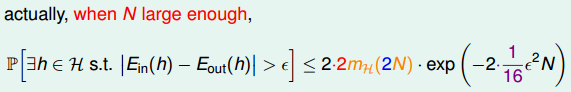
推导如下：

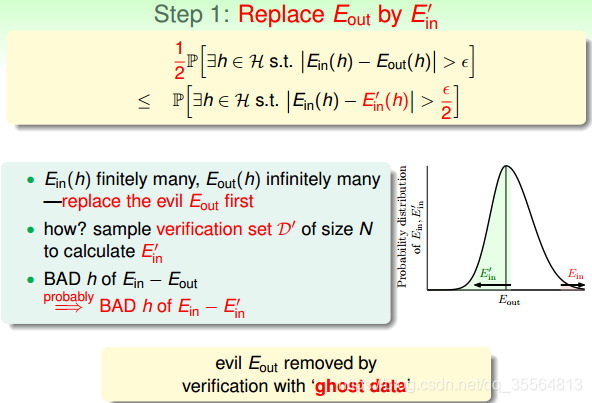
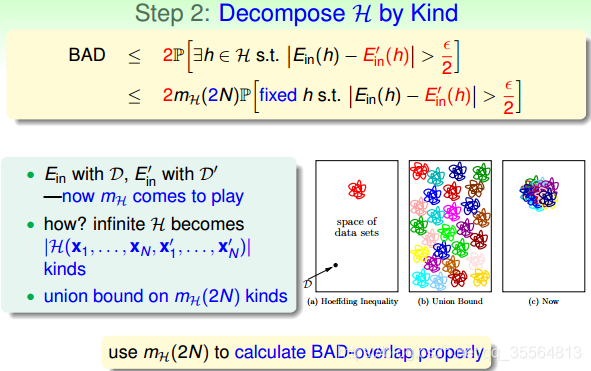
得到最后的VC bound：

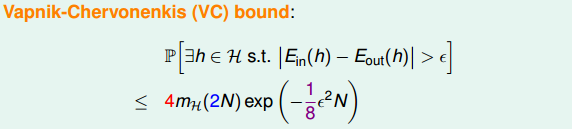
对于已知的2D perceptrons，它的break point是4，那么成长函数 $m_H(N)=O(N^3)$ 。所以，我们可以说2D perceptrons是可以进行机器学习的，只要找到hypothesis能让 $E_{in}\approx0$ ，就能保证 $E_{in}\approx E_{out}$ 。

总结

本节课我们主要介绍了只要存在 break point，那么其成长函数 $m_H(N)$ 就满足 poly(N)。推导过程是先引入 $m_H(N)$ 的上界 B(N,K)，B(N,K) 的上界是 N 的 k−1阶多项式，从而得到 $m_H(N)$ 的上界就是 N 的k−1阶多项式。然后，我们通过简单的三步证明，将 $m_H(N)$ 代入了 Hoffding 不等式中，推导出了 Vapnik-Chervonenkis(VC) bound，最终证明了只要 break point 存在，那么机器学习就是可行的。