Coursera机器学习基石笔记week7

The VC Dimension

Definition of VC Dimension

在这里插入图片描述
VC dimension就是满足成长函数 $2^N$ 的最大的N。也就是 $d_{vc}$ =‘minimum k’-1.

VC Dimension of Perceptrons

已知在1D Perceptron， $d_{vc}=2$ ，在2D Perceptrons， $d_{vc}=3$ ，那么我们有如下假设： $d_{vc}=d+1$ ，其中d为维数。如果我们要证明的话，需要分为两步：

$d_{vc}\geq d+1$
$d_{vc}\leq d+1$

首先证明 $d_{vc}\geq d+1$ ：

在d维里，我们只要找到某一类的d+1个inputs可以被shatter的话，那么必然得到 $d_{vc}\geq d+1$ 。所以，构造一个d维的矩阵X能够被shatter就行。X是d维的，有d+1个inputs，每个inputs加上第零个维度的常数项1（threshold），得到X的矩阵：
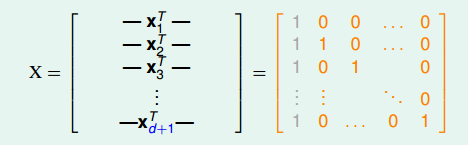
在这里插入图片描述
这是一个(d+1)*(d+1)的矩阵，且有d+1组线性无关向量，则该矩阵是非奇异的，也就是可逆的。shatter的本质是假设空间H对X的所有情况的判断都是对的，即总能找到权重W，满足 $X\ast W=y$ ， $W=X^{-1}\ast y$ 。因为可逆针对任意一个y都可以由X矩阵得到对应的权重w。那么说明 $d_{vc}\geq d+1$ 。

然后证明 $d_{vc}\leq d+1$ :

那么需要证明对于任意d+2个inputs无法被shatter，那么就可以证明不等式成立。我们构造一个任意的矩阵X，其包含d+2个inputs，该矩阵有d+1列，d+2行。这d+2个向量的某一列一定可以被另外d+1个向量线性表示，例如对于向量Xd+2Xd+2，可表示为：
$X_{d+2}=a_1∗X_1+a_2∗X_2+⋯+a_{d+1}∗X_{d+1}$

其中，假设a1>0，a2,⋯, $a_{d+1}$ <0

那么如果 $X_1$ 是正类， $X_2,⋯,X_{d+1}$ 均为负类，则存在W，得到如下表达式：
$X_{d+2}∗W=a_1∗X_1∗W+a_2∗X_2∗W+⋯⋯+a_{d+1}∗X_{d+1}∗W>0$
因为其中 $X_1$ 大于0，代表正类； $X_2,X_3…….X_{d+1}$ 小于0，代表负类。所有对于这种情况， $X_{d+2}$ 一定是正类，无法得到负类的情况。也就是说，d+2个inputs无法被shatter。

因此可以证明 $d_{vc}=d+1$

Physical Intuition of VC Dimension

在这里插入图片描述
w又可以叫做自由度，就像是上图中的旋钮一样可以自由的调节。

vc dimension又代表了可以产生dichotomy 的数量。

扫描二维码关注公众号，回复： 4009800 查看本文章

Interpreting VC Dimension

已知VC bound：
在这里插入图片描述
我们让 $\delta$ 等于VC bound。那么我们想要得到好的情况，那么：

经过上述计算，我们推导出了 $\epsilon$ 的值。ϵ表现了假设空间H的泛化能力，ϵ越小，泛化能力越大。

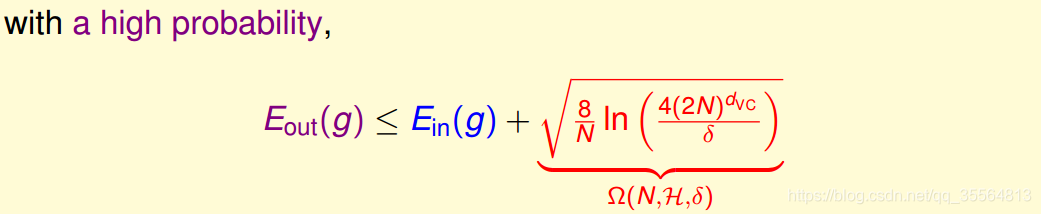
上图，红色部分代表了模型复杂度，其与样本数量N， $d_{vc}$ ， $\delta$ 有关。根据上图的关系，我们可以绘出相关的趋势：
在这里插入图片描述
根据上述趋势，我们不能一味的减小 $E_{in}$ 的值，因为随着 $E_{in}$ 的变小，模型复杂度在变大，导致泛化能力变小，导致 $E_{out}$ 先变大再变小。

根据以上图片可以看出，在 $d_{vc}$ 固定时，N理论上需要是 $d_{vc}$ 的10000倍。但是实际上只需要是 $d_{vc}$ 的10倍就好了，那么为什么呢？因为其实vc bound太松了，它其实比真正的上界大得多。
在这里插入图片描述
vc bound从以上一步步推导而来，导致上界不断变松。但是想要对其收紧确实比较困难，但是幸亏vc bound基本上对所有模型的宽松程度是相似的，那么我们可以通过比较不同的模型进行比较。

总结

本节课主要介绍了VC Dimension的概念就是最大的break point-1。然后，我证明了Perceptrons在d维度下的VC Dimension是d+1。接着，我们在物理意义上，将 $d_{vc}$ 与自由度联系起来。最终得出结论 $d_{vc}$ 不能过大也不能过小。选取合适的值，才能让Eout足够小，使假设空间H具有良好的泛化能力。模型复杂度是会随着 $d_{vc}$ 的变大不断变大的。vc bound其实是比较宽松的，我们不需要利用理论上的样本复杂度。