【深度学习】Softmax回归（一）概念和原理

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qq_28869927/article/details/84972720

概述

在前面的三篇文章中：

• 【深度学习】线性回归（一）原理及python从0开始实现
• 【深度学习】线性回归（二）小批量随机梯度下降及其python实现
• 【深度学习】线性回归（三）使用MXNet深度学习框架实现线性回归

介绍了线性回归的基本原理，自己动手使用Python从0开始做了实现，同时也借助MXNet深度学习框架进行了实现，并在一个公开数据集和一个仿真数据集上进行了实验。

在机器学习问题中，我们通常将对连续值处理的模型叫做回归模型，对离散值处理的模型叫做分类模型。可以看到，线性回归正是适用于输出为连续值的情况。在某些场景中，模型的输出可能是诸如瓜的类别、图像类别等的离散值。比如输入一张包含西瓜或哈密瓜的图片，我们需要输出图片中包含哪种瓜，我们一般使用离散的值来描述这种类别，比如0代表西瓜，1代表哈密瓜。

这时我们可以采用分类模型来进行处理，比如Softmax线性分类模型（也称Softmax回归）。笔者也正通过《动手学深度学习》这本在线书籍学习Softmax模型，借此将学习笔记和心得记录与此，希望可以和大家相互交流。

Softmax

Softmox回归模型

我们以上文提到的瓜的类别问题为例：

• 假设输入图片的大小为 $2*2$，即包含4个像素，每个像素是一个特征；
• 假设需要判断图片中是哪种类型的瓜，以 $y_1=1$代表西瓜， $y_2=2$代表哈密瓜， $y_3=3$代表木瓜；

Softmax和线性回归一样，均对输入特征做线性叠加。与线性回归不同的是，Softmax输出值的个数等同于样本中的类别数，所以我们得到( $o_n$表示模型的输出)：

$\left \{ \begin{array}{c} \ o_1=x_1w_{11}+x_2w_{21}+x_3w_{31}+x_4w_{41}+b_1 \\ \\ \ o_2=x_1w_{12}+x_2w_{22}+x_3w_{32}+x_4w_{42}+b_2 \\ \\ \ o_3=x_1w_{13}+x_2w_{23}+x_3w_{33}+x_4w_{43}+b_3 \end{array} \right.$

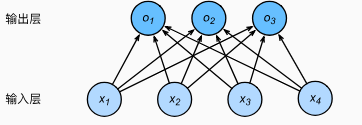
Softmax和线性回归一样，也可以看做是单层神经网络，并且输出层也是全连接层，因为 $o_n$依赖于所有的输入 $x_n$。画出上述模型的神经网络结构如下：

矢量形式

为了方便计算，我们将上述模型写成矢量形式。令：
$\boldsymbol x= \begin{bmatrix} x_1 & x_2 & x_3 & x_4 \\ \end{bmatrix} , \boldsymbol W= \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ w_{41} & w_{42} & w_{43} \\ \end{bmatrix} , \boldsymbol b= \begin{bmatrix} b_1 & b_2 & b_3 \\ \end{bmatrix} , \boldsymbol o= \begin{bmatrix} o_1 & o_2 & o_3 \\ \end{bmatrix}$
得：
$\boldsymbol o=\boldsymbol x \boldsymbol W + \boldsymbol b$

Softmax运算

模型解决了，就该解决数据的预处理问题了。一般情况下，我们需要对神经网络的输入值和输出值做特定的处理，使其符合某种特定的概率分布但又不改变其特征，从而便于作为模型的输入和输出。

一个例子是我在【深度学习】Python实现简单神经网络一文中，利用单隐藏层神经网络处理MNIST数据集时的数据预处理方法：

• 输入特征是784个像素值，每个像素的取值范围为[0,255]。为了使输入满足sigmoid激活函数的优良工作区间，将输入像素值的范围缩放至[0.01,1.0]的范围（不包含0是为了避免0值输入）；
• 样本标签包含0~9共10个数字，即输出层包含10个节点，类似于上述的瓜分类问题；
• 采用“激发”或者叫做“置信度”的方式从输出进行分类，比如10个节点的输出值为：[0.01, 0.01, 0.01, 0.98, 0.01, 0.01, 0.02, 0.01, 0.03, 0.01]，我们判断输入图片包含数字“3”。

在这里我们采用类似的思想，在瓜分类问题中，Softmax模型输出 $o_1, o_2, o_3$的值分别为 $0.1, 10, 0.1$时，认为预测类别是2，即代表哈密瓜。

然而，直接使用输出层的输出值将存在问题：

1. 输出值的范围不确定，我们很难直观判断这些值的意义，比如当输出1000, 10, 1000时。
2. 由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以估计。

Softmax运算符（Softmax operator）就是将输出值变换成值为正且和为1的概率分布，定义为：
$\hat y_1, \hat y_2, \hat y_3=softmax(o_1, o_2. o_3)$
其中：
$\hat y_n=\frac{exp(o_n)}{\sum_{i=1}^n{exp(o_i)}}$
从定义可以看到： $\hat y_1+ \hat y_2+ \hat y_3=1且0\le \hat y_1, \hat y_2, \hat y_3 \le 1$，且 $\hat y_i和o_i$的大小关系一致。Softmax运算不改变预测类别的输出。

从而得到：
$\boldsymbol {\hat y}=softmax(\boldsymbol o)$

交叉熵损失函数

真实标签的变换

同【深度学习】Python实现简单神经网络一文中相同的数据预处理道理，既然我们使用softmax运算将模型的输出值做了变换，我们还需要对样本中的标签做相应的变换，以方便损失（或者误差）的计算。

在这个瓜分类的例子中，我们将真实标签用类似的分布表示：对于样本 $i$，构造一个3维向量 $\boldsymbol y^{(i)}$（因为有3个类别，3个输出节点），使得其第 $y^{(i)}$个元素为1，其余为0。即如果一个样本的真实标签为西瓜，我们就使用3维向量 $\boldsymbol y=[1.0, 0, 0]$来表示。

平方损失函数

类似于线性回归，这个例子中的平方损失函数表示为: $||\boldsymbol {\hat y^{(i)}}-\boldsymbol y^{(i)}||^2/2$。尽管我们可以使用这个损失函数来调整模型的参数，但是在这个问题中，我们并不需要预测值完全等同于真实值。比如，某个样本的真实标签为 $[0, 0, 1.0]$，我们的预测值为 $[0.2, 0.1, 0.7]$也可以预测正确，判断这个样本属于木瓜。这样一来，平方损失函数却显得过于“严格”了。

交叉熵损失函数

鉴于平方损失函数在这种情况下的不足，一个改善的方法是使用更加适合衡量两种概率分布差异的测量函数。其中，交叉熵（cross entropy）是一个常用的方法， $q$表示输出值个数（类别数）：
$\boldsymbol H(\boldsymbol y^{(i)} , \boldsymbol {\hat y^{(i)}}) \ =-\sum_{j=1}^qy_j^{(i)}log\hat y_j^{(i)}$
其中带下标的 $y_j^{(i)}$不同于 $y^{(i)}$， $y_j^{(i)}$表示向量 $\boldsymbol y^{(i)}$中的非0即1元素，所以 $\boldsymbol y^{(i)}$中的第 $y^{(i)}$个元素表示为 $y_{y^{(i)}}^{(i)}且y_{y^{(i)}}^{(i)}=1$，其余元素为0。故而上述交叉熵可以简化为：
$\boldsymbol H(\boldsymbol y^{(i)} , \boldsymbol {\hat y^{(i)}})=-log \hat y_{y^{(i)}}^{(i)}$
显然，当一个样本属于不止一个类别时（即一个样本可能同时包含西瓜和哈密瓜），不能做如上简化。

当一个样本的容量为 $n$时，交叉熵验证函数表示为：
$loss(\boldsymbol \Theta)=\frac1n\sum_{i=1}^n\boldsymbol H(\boldsymbol y^{(i)} , \boldsymbol {\hat y^{(i)}})$
其中， $\boldsymbol \Theta$表示模型参数。最小化 $loss(\boldsymbol \Theta)$等价于最大化 $exp(-nloss(\boldsymbol \Theta))=\prod_{i=1}^n\hat y_{y^{(i)}}^{(i)}$。如果我们将模型的输出值看作是对某个类别的预测概率的话，则最小化交叉熵函数等价于最大化训练数据集所有标签类别的联合预测概率。