深度学习笔记：3.8-3.9 softmax回归

3.8 介绍：softmax 回归

softmax回归虽然叫‘回归’，但和logistic回归一样，其实是分类问题，和logistic回归不同的是， logistic回归是二分类问题，而softmax回归解决的是多分类问题，如下图所示：

假设我们需要学习器将图片分类，1表示猫，2表示狗，3表示小鸡，0表示其他。在softmax回归中，类别数C=4，输出层我们也称为softmax layer。既然是多分类问题，我们希望输出的结果是分为不同类别的概率，且希望概率和为1，如上图所示，我们希望softmax layer第一个节点输出x属于其他的概率，第二个节点输出x属于猫的概率等，输出层节点个数就是类别个数，即 $\widehat{Y}$ 是一个4维向量。

softmax layer具体计算过程如下图所示：

因为希望概率和为1，所以softmax layer采用了softmax激活函数，不同于其他激活函数，它的作用就是保证概率和为1。

具体实现如上图所示：通过上一层 $a^{[L-1]}$ 计算得到 $Z^{[L]}$ ， $Z^{[L]}$ 是一个4维向量，对 $Z^{[L]}$ 的每一个元素进行指数操作(elementwise)，记为临时变量t，t也是一个4维向量，令 $a^{[L]}=\frac{e^{Z^{[L]}}}{\sum_{j=1}^{4}t_{j}}$ ， $a^{[L]}$ 也是一个4维向量，具体为 $a_{i}^{[L]}=\frac{e_{i}^{Z^{[L]}}}{\sum_{j=1}^{4}t_{j}}$ 。通过softmax激活函数，得到满足条件的输出结果 $a^{[L]}$ ，即每一个元素表示分为某一类别的概率，且所有元素和相加为1。具体实例如上图右侧所示。

softmax激活函数相比其他激活函数特殊的地方在于，比如ReLU和sigmoid激活函数每次都是处理一个实数值(real value)，且输出一个实数值，但是softmax激活函数作用的对象是向量，输出的结果也是向量，且该向量的维度是多分类的类别数。

这里列了一些没有隐藏层的神经网络softmax多分类的分类结果，如下图所示。

在没有隐藏层的情况下，softmax分类器是线性分类器，就像logistic回归一样，LR也是一个线性分类器，且针对二分类。LR为什么是线性分类器，这里简单讲一下。前提假设 $P(Y=1|X)=\frac{e^{W^{T}X}}{1+e^{W^{T}X}}$ ， $P(Y=0|X)=\frac{1}{1+e^{W^{T}X}}$ 。若 $P(Y=1|X)>P(Y=0|X)$ ，即 $\frac{P(Y=1|X)}{P(Y=0|X)}>1$ ，则将X判为正类，而 $\frac{P(Y=1|X)}{P(Y=0|X)}=e^{W^{T}X}$ ，两边取对数得， $W^{T}X>0$ ，即若 $W^{T}X>0$ ，就把X分为正类，可见LR分界面为线性分界面，所以LR是线性分类器。

softmax分类器也是同理，因为softmax激活函数做的变换也是指数变换，只不过要选取概率最大的那一类，这就需要两两比较，所以如上图所示，每两类之间分界面都是线性的，比如第一类和第二类比较，分界面是 $(W_{1}-W_{2})^{T}X>0$ 。

当然如果神经网络加入很多隐藏层，我们就可以得到更加复杂的非线性分界面了。

3.9 实战：如何训练softmax分类器

上图用实例表现了softmax激活函数的工作，3.8节我们也已经详细描述过了，这里主要讲一下为什么我们称其为‘softmax’。‘softmax’对应于‘hardmax’，因为softmax回归其实是多分类问题，所以hardmax指的是输出结果不是概率，而直接就是0或1，1表示属于这一类，0表示不属于，对应与hard的soft表示的就是输出结果为概率啦。那max在这里表示什么呢？这个对应于激活函数中我们做指数变换，因为指数函数是单增函数，所以其实 $Z_{i}^{[L]}$ 越大，他所对应的 $a_{i}^{[L]}$ 就越大，因为分母都一样，如上图实例中元素5，这就是softmax中max含义。

softmax回归其实是logistic回归由二分类向多分类的推广，因为应用于没有隐藏层的神经网络，这二者都是线性分类器(3.8已证明)，本质上也可以表现这一点。而当softmax回归中的种类个数C等于2时，softmax回归也就退化成logistic回归，因为按照softmax回归方法去计算X归属于两类的概率，因为只有两类且概率和为1，所以也可以直接按照logistic回归方法，即x归属另一类概率为1-y，两种方法本质是一样的。

既然softmax回归是logistic回归的推广，那softmax回归的loss function是怎样的呢？如下图所示：

老师这里通过实例给误差函数一种intuition的理解方式，即loss function如上图 $L(\widehat{y},y)$ 所示，还是3.8中的例子，假设我们的实际label是(0;1;0;0)，即图片中是一只猫，但预测结果是(0.3;0.2;0.1;0.4)，即预测该图片是一只猫的概率是0.2，预测结果很不好。loss function的intuition理解是怎么的呢？我们定义的损失函数如上图所示，在图片是猫的情况下， $y_{1}=y_{3}=y_{4}=0$ ， $L(\widehat{y},y)$ 就变为 $-log(\widehat{y_{2}})$ ，我们希望损失函数值越小越好，那就是希望 $\widehat{y_{2}}$ 能够越大越好，也就是将图片预测为猫的概率越大越好，这一切分析是说得通的。

但我想从数学层面来讲一下这里损失函数的定义方法，理解LR损失函数的同学应该能够很容易理解这里为什么这么定义，所以我先讲一下LR损失函数的定义方法。为了更好地过渡到多分类问题，这里定义使用老师的定义方法，即 $\widehat{y_{j}}$ 表示将X判为第j类的概率， $y_{j}$ 表示X真实label。在LR问题中，我们直觉会希望 $\widehat{y_{1}}^{y_{1}}\widehat{y_{2}}^{y_{2}}$ 值越大越好，因为若X属于第一类， $\widehat{y_{1}}^{y_{1}}\widehat{y_{2}}^{y_{2}}$ = $\widehat{y_{1}}$ ，即我们希望X预测为第一类的概率越高越好，同理预测为第二类也是这样。然后对 $\widehat{y_{1}}^{y_{1}}\widehat{y_{2}}^{y_{2}}$ 作log处理，得到 $\sum_{j=1}^{2}y_{j}log\widehat{y_{j}}$ ，即我们希望这个值越大越好，但一般损失函数我们都希望越小越好，求最小值，所以这里取相反数，即loss function为 $-\sum_{j=1}^{2}y_{j}log\widehat{y_{j}}$ ，同多分类loss function相同，背后的数学思想就是这样的。

当然这个loss function表示形式针对的是一个X，对于所有样本，目标函数还要对m个样本求和得到J，如上图所示，所以我们的目标就是求目标函数的最小值。

注意真实label Y矩阵和 $\widehat{Y}$ 矩阵的不同，Y矩阵的每一列是样本m所属类别的one-hot编码，除了所属类别为1，其余位置都为0，而

$\widehat{Y}$ 矩阵的每一列就是样本m输出结果，表示将样本判为每一类别的概率。

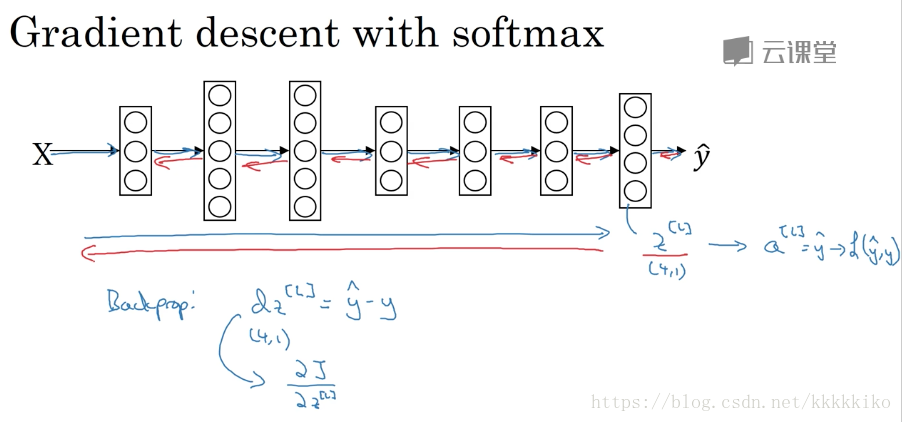
接下来讲一下softmax在神经网络中实现梯度下降，如下图所示：

向前传播还好，其实主要是向后传播梯度如何计算，在softmax回归中，通过softmax激活函数将 $Z^{[L]}$ 变为 $a^{[L]}$ ， $a^{[L]}$ 就是loss function中 $\widehat{y}$ 。之前在backprop选修那一小节，老师推导过LR情况下(即最后一层激活函数是sigmoid) $dZ^{L}=\widehat{y}-y$ ，softmax情况下也是一样，我们来推导一下。

直接将 $a^{[L]}$ 值代入 $L(\widehat{y},y)$ 得到 $L(\widehat{y},y)$ 与 $Z^{[L]}$ 的关系式，即 $L(\widehat{y},y)=-\sum_{i=1}^{4}y_{i}log\frac{e^{Z_{i}^{[L]}}}{\sum_{i=1}^{4}e^{Z_{i}^{[L]}}}$ ，L对 $Z_{i}^{[L]}$ 求导得 $\frac{e^{Z_{i}^{[L]}}}{\sum_{i=1}^{4}e^{Z_{i}^{[L]}}}-y_{i}$ ，所以 $dZ^{[L]}=\widehat{y}-y$ 。梯度结果也在本质上反映出softmax回归是logistic回归的推广。

若我们使用深度学习框架，可以不考虑向后传播，只要保证正确进行向前传播，框架可以直接计算梯度下降需要的梯度。