深度学习笔记------softmax回归

分类问题

我们希望我们可以通过某一些的事物特征来判断这一类事物的类别，但这些类别往往不是"非黑即白"，可能有多种类别，这些类别之间的关系是离散的，这时我们需要一种模型来区分这一类特征的类别。当然也存在多种相似的类别，它们对于相关属性的反映相似，但是终究是有差距的，所以最终我们往往取的是对其拟合程度最好的一种类别来对其特征进行标记。

预测模型

模型的输入是相关训练集的各个属性，在这里也是以一种线性叠加的方式来进行构建，即：
$x_1 \omega_1+x_2 \omega_2+.......+x_n \omega_n+b=o$
$\omega$为相关的权重系数，x为具体的属性值，b为一个相应的偏移量，但是这里与线性回归的不同在于这个 $o$不在是一个简单的预测值，其实际的意义产生了变化，其名称代表了一个类别，其值的大小代表了这些属性对于这一类别的匹配程度，值越大，匹配程度越高（含负值，负值的绝对值越大匹配程度越低，这个在后面的评价函数中体现）。
因此对应的我们要实现知道这种分类模型有多少个类别，对每一个类别都建立一个这样的关系，于是有完整的预测模型：
$x_1 \omega_{11}+x_2 \omega_{12}+.......+x_n \omega_{1n}+b_1=o_1$
$x_1 \omega_{21}+x_2 \omega_{22}+.......+x_n \omega_{2n}+b_2=o_2$
$x_1 \omega_{31}+x_2 \omega_{32}+.......+x_n \omega_{3n}+b_3=o_3$
$..........$
$x_1 \omega_{d1}+x_2 \omega_{d2}+.......+x_n \omega_{dn}+b_d=o_d$
将x进行扩展有 $X=[x_1,x_2,...x_n,1]$，同样的对于 $\omega$有 $w_i=[w_{i1},w_{i2},w_{i3},...w_{in},b_i]$
$\begin{bmatrix}w_{11} & w_{12} &....&w_{1d} & b_1\\ w_{21} & w_{22} &....&w_{2n} & b_2\\ .... & .... &....&.... & ....\\ w_{d1} &w_{d2} &....&w_{dn} & b_d\end{bmatrix}$ $\begin{bmatrix}x_1 \\ x_2\\....\\ 1\end{bmatrix}=\begin{bmatrix}\ o_1 \\ o_2\\....\\ o_d\end{bmatrix}$
大致如下图，有一个输入层一个输出层，输出层也是一个全连接层，每个输出结果都依赖所有的输入数据。

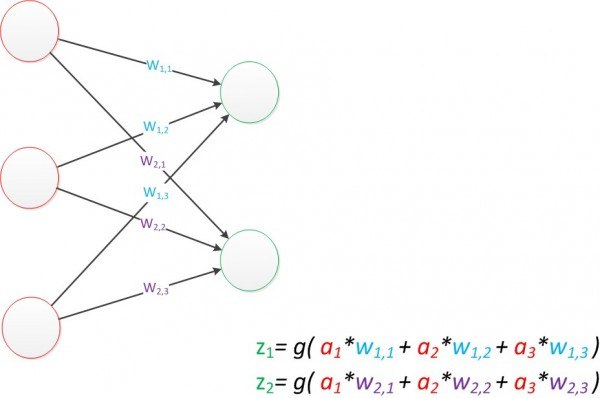
通过这个模型，我们通过输出层中数值大小来判断具体的类别归属。比如 $o1,o2,o3$为1,2,3最大的为 $o3$，所以最终的类别为 $o_3$对应的类别。

softmax函数

显然在上面的输出中我们对于结果的表示体现不真切，很难具体的描述各个类别的匹配程度，并且 $o_i$也可能取到负值，很难对其进行相关的意义描述，所以我们需要对其进行归一化，将其产生的结果映射到0~1之间，来更真切的表示其属性对某一类型匹配的置信度。相关函数如下：
将获得的 $o_1,o_2,....o_d$转变为指数形式为 $e^{o_i}$，这样不论 $o_i$的取值如何都将对应到正值，之后再进行一个归一化，即 $\hat{y_i}=\frac{e^{o_i}}{\sum_{i=1}^{d}e^{o_i}}$，表示关于某类别预测的置信度。显然对于 $\sum_{i=1}^{d}\hat{y_i}=1$，最终的标记类别为 $max(\hat{y_i})$。
因此softmax函数只是将对应的输出结果进行一个整合，将其输出数据的意义体现为一个概率分布，并不影响实际的输出类别。

评价模型

实际获得的输出为一个概率分布表示各个类别的置信度，而对于某个测试实例，实际的标签值中只有一个标签为1，其他的标签的值均为0。我们需要使我们的输出数据更加贴近与实际的标签值。

交叉熵损失函数

由于我们实际取的是最大置信度的那个标签，所以我们不需要预测的概率与实际完全相同，所以有交叉熵这样一个评估方法：
$H(y_i,\hat{y_i})=-\sum_{i=1}^{d}y_ilog\hat{y_i}$
其中 $y_i$为实际的标签值，非1即0，而 $\hat{y_i}$为我们得到的输出参数，即各个标签的概率分布，显然对于 $y_i$中为0的值来说 $y_ilog\hat{y_i}=0$，所以在一个样本一个标签的情况下，我们仅仅考虑标签值 $y_i=1$时对于的 $y_ilog\hat{y_i}$即可，由于 $log\hat{y_i}$中 $\hat{y_i}<0$，所以前面有一个负号为 $-log\hat{y_i}$。
对于m个样本训练集来说实际的损失函数为：
$\ell(\theta)=\frac{1}{n}\sum_{i=1}^{m}H(y_i,\hat{y_i})=-\frac{1}{n}\sum_{i=1}^{m}log\hat{y_i}$
变换一下有：
$e^{-n\ell(\theta)}=\prod_{i=1}^{m}\hat{y_i}$
要使 $\ell(\theta)$最小即相应的 $\prod_{i=1}^{m}\hat{y_i}$取最大。

分类的准确率：实际运行时我们将模型得到的分类结果与实际进行比对，求出预测正确的数量占整个预测数据集的比值。