积性函数前缀和问题

1. 求前n个正整数的约数之和

即 $\sum_{i=1}^{n}\sigma (i) , i<=10^{12} , \sigma (n)=\sum_{d|n}^{ }d$ .

解：

$\sum_{i=1}^{n}\sigma (i) =\sum_{i=1}^{n}\sum_{d|i}^{ }d=\sum_{i=1}^{n}\sum_{d=1}^{n}[d|i]*d=\sum_{i=1}^{n}i*\sum_{d=1}^{n}[i|d]=\sum_{i=1}^{n}i*\left \lfloor \frac{n}{i} \right \rfloor$

或 $\sum_{i=1}^{n}\sum_{d|n}^{ }d=\sum_{i=1}^{n}\sum_{d=1}^{\left \lfloor \frac{n}{i} \right \rfloor}d=\sum_{i=1}^{n}\frac{(1+\left \lfloor \frac{n}{i} \right \rfloor)*\left \lfloor \frac{n}{i} \right \rfloor}{2}$

需要说明的是 $\sum_{i=1}^{n}\frac{(1+\left \lfloor \frac{n}{i} \right \rfloor)*\left \lfloor \frac{n}{i} \right \rfloor}{2}=\sum_{i=1}^{n}i*\left \lfloor \frac{n}{i} \right \rfloor$ 是一种常见的表示形式。

当 $i<\sqrt{n}$ 时， $\left \lfloor \frac{n}{i} \right \rfloor$ 显然只有 $O(\sqrt{n})$ 个取值，当 $i>\sqrt{n}$ 时， $\left \lfloor \frac{n}{i} \right \rfloor<\sqrt{n}$ ，显然也只有 $O(\sqrt{n})$ 个取值。当 $\left \lfloor \frac{n}{i} \right \rfloor$ = k (常数) 时，i的取值区间是 $[\left \lfloor \frac{n}{k+1}\right \rfloor+1,\left \lfloor \frac{n}{k}\right \rfloor]$ ，因此可以用 $O(\sqrt{n})$ 复杂度求解。

code：

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

typedef long long ll;
 
ll n,i,a,b;
ll sum;
 
int main(){
	scanf("%lld",&n);
	sum = 0;
	for(i=1;i*i<=n;i++){
		sum += i * (n / i);
		b = n/i;
		a = n/(i+1)+1;
		sum += (a+b) * (b-a+1) / 2 * i;
	}
	i--;
	if (i*i == n)
		sum -= i * (n / i);
	printf("%lld\n",sum);
	return 0;
}

2.求 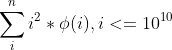$\sum_{i}^{n}i^{2}*\phi (i),i<=10^{10}$

设 $f(x)=x^{2}*\phi (x)$ ， $g(x)=x^{2}$ .

所以，两个函数的狄利克雷卷积 $(f*g)(n)=\sum_{d|n}^{ }d^{2}*\phi (d)*(\frac{n}{d})^{2}=n^{3}$ .

$\therefore \sum_{i=1}^{n}\sum_{d|i}^{ }d^{2}*\phi (d)*(\frac{i}{d})^{2}=\sum_{i=1}^{n}i^{3}$

$\therefore \sum_{i=1}^{n}i^{2}\sum_{d|i}^{ }d^{2}*\phi (d)=\sum_{i=1}^{n}i^{3}$

$\therefore \sum_{i=1}^{n}i^{2}\sum_{d=1}^{\left \lfloor \frac{n}{i} \right \rfloor}d^{2}*\phi (d)=\sum_{i=1}^{n}i^{3}$

$\therefore \sum_{i=1}^{n}i^{2}*S(\left \lfloor \frac{n}{i} \right \rfloor)=\sum_{i=1}^{n}i^{3}$

$\therefore S(n)+\sum_{i=2}^{n}i^{2}*S(\left \lfloor \frac{n}{i} \right \rfloor)=\sum_{i=1}^{n}i^{3}$

$\therefore S(n)=\sum_{i=1}^{n}i^{3}-\sum_{i=2}^{n}i^{2}*S(\left \lfloor \frac{n}{i} \right \rfloor)$ （杜教筛求解）

其中： $1^{2}+2^{2}+3^{2}+...+n^{2}=\frac{n*(n+1)*(2n+1)}{6}$ ， $1^{3}+2^{3}+3^{3}+...+n^{3}=(\frac{n*(n+1)}{2})^{2}$ .

code：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int MAX = 1e7;
const ll MOD = 1000000007;

ll n,p;
ll phi[MAX+10],prime[MAX+10];
bool check[MAX+10];

inline ll read()
{
    register ll x=0,t=1;register char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')t=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
    return x*t;
}

ll extendGcd(ll a, ll b, ll &x, ll &y) {
	ll ans, t;
	if (b == 0) {
		x = 1; y = 0;
		return a;
	}
	ans = extendGcd(b, a%b, x, y);
	t = x; x = y; y = t - (a / b)*y;
	return ans;
}

ll inv(ll a, ll m) {
	ll x, y, d;
	d = extendGcd(a, m, x, y);
	if (d == 1)
		return (x%m + m) % m;
	else
		return -1;
}

void get_sum()
{
    memset(check,false,sizeof(check));
    phi[1]=1;
    int tot=0;
    for(int i=2;i<=MAX;i++){
        if(!check[i]){
            prime[tot++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<tot&&i*prime[j]<=MAX;j++){
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else{
                phi[i*prime[j]]=phi[i]*phi[prime[j]];
            }
        }
    }
    for(ll i=2;i<=MAX;i++)
        phi[i]=(phi[i-1]+phi[i]*(i*i%p))%p;
}

map<ll,ll>dp;

ll inv2;
ll inv6;

ll get(ll x,ll y)
{
    x=(x-1)%p;
    y%=p;
    ll tmp1=y*(y+1)%p*(2*y+1)%p*inv6%p;
    ll tmp2=x*(x+1)%p*(2*x+1)%p*inv6%p;
    ll ans=(tmp1-tmp2+p)%p;
    return ans;
}

ll gett(ll x)
{
    x%=p;
    ll ans=x*(x+1)%p*inv2%p;
    ans=ans*ans%p;
    return ans;
}

//所求前缀和
ll cal(ll x)
{
    if(x<=MAX)   return phi[x];
    if(dp[x])   return dp[x];
    ll pos;
    ll tmp=0;
    for(ll i=2;i<=x;i=pos+1){
        pos=x/(x/i);
        tmp+=get(i,pos)*cal(x/i)%p;
        tmp%=p;
    }
    dp[x]=gett(x)-tmp;
    return dp[x];
}

//洛谷3768
int main()
{
    p=read();
    n=read();
    inv2=inv(2,p);
    inv6=inv(6,p);
    get_sum();
    ll pos;
    ll ans=0;
    for(ll i=1;i<=n;i=pos+1){
        pos=n/(n/i);
        ans=(ans+gett(n/i)*((cal(pos)-cal(i-1)+p)%p)%p)%p;
    }
    printf("%lld\n",ans);
    return 0;
}