吴恩达深度学习总结(6)

mini-batch gradient descent

定义

mini-batch实质上是将训练集切分为 $T$ 部分，不再一次训练整个训练集而是 $T$ 个子训练集依次训练。
训练过程中， $epoch$ 表示训练一次整个训练集， $batch$ 是指训练一次 $X^{t}$。

优点

如果一次只训练一个样本，除了迭代次数太多且失去了向量化的加速之外，在使用SGD进行优化时可能无法实现收敛。
如果一次训练了所有样本，消耗的内存过大，且难以处理。
使用 $T \neq 1\;or\; m$$，虽然损失函数不会呈现一直下降，但是总体会有下降的趋势，趋于收敛。
若在训练过程中，画出的损失函数曲线波动幅度较大，说明batch的尺寸过小，应适当增大batch-size。

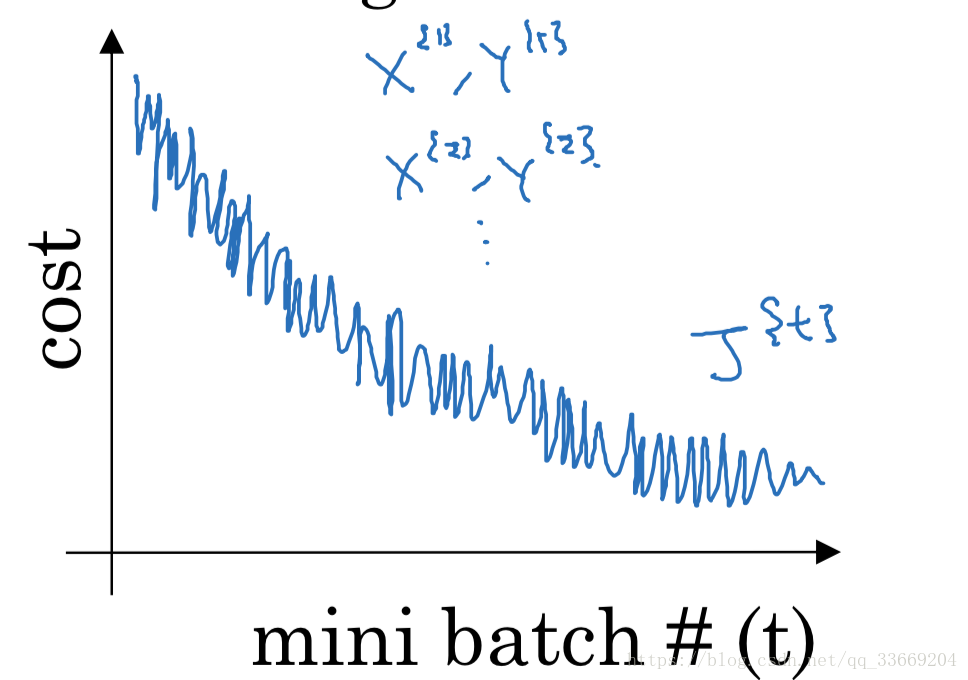
（图片来自吴恩达课件）
mini-batch size的取值通常为2的指数倍（如 64，128，256…），吴恩达课程中提出，如果训练集的大小 $m$ 小于2000，那么可以直接训练。

Gradient Descent with momentum

基本思想

计算梯度的指数加权平均，并用该值来更新权重

流程

1. 基于backwards计算 $dW$， $db$
2. 根据给定的 $\beta$，计算 $v_{dW} = \beta v_{dW} + (1-\beta)dW$
   $v_{db} = \beta v_{db} +(1-\beta) db$
   $W = W - \alpha v_{dW}, b = b - \alpha v_{db}$
   这里 $\beta$ 通常设为 0.9。
   应用指数加权平均时，本身应该有一个偏差修正的过程，但在实际应用时通常不引入该方法。

加权指数平均介绍

$V_t = \beta V_{t-1} + (1- \beta) \theta_t$
通常认为权重小于 $\frac{1}{e}$ 的值对最终结果的影响可以忽略不计，而 $\beta^{\frac{1}{1-\beta}} \approx \frac{1}{e}$，因此加权指数平均认为是 $\frac{1}{1-\beta}$ 个值的加权平均。
偏差修正：由于一开始的数据的预先变量较少，因此加权指数平均的效果较差，于是引入偏差修正，使预测更为准确。
$\frac{V_t}{1-\beta^t}$
随着 $t$ 的增大，偏差修正的影响越来越小。

直观理解

这里引用 monitor1370的观点：

1. 当本次梯度下降的方向与上次更新量的方向相同时，上次的更新量能够对本次的搜索起到一个正向加速的作用。
2. 当本次梯度下降的方向与上次更新量的方向相反时，上次的更新量能够对本次的搜索起到一个反向减速的作用。

RMSprop（Root Mean Square prop）

基本思想

在权重更新时，我们更希望权重能按照绿色线的方向逼近最优点，但实际上权重更多是按照蓝色线更新。假设垂直方向为 $db$，水平方向为 $dW$，那么我们只要减缓 $db$ 的变化，增大 $dW$ 的变化就可以更好的逼近最优点。

流程

1. 基于backwards计算 $dW$， $db$
2. $S_{dW} = \beta S_{dW} + (1-\beta) d^2W$ $S_{db} = \beta S_{db} + (1-\beta) d^2b$由于 $db$ 通常比 $dW$ 大，所以 $S_{dW}$ 通常比 $S_{db}$ 小。
3. $W = W-\alpha \frac{dW}{\sqrt{S_{dW}+ \epsilon}}$ $b = b-\alpha \frac{db}{\sqrt{S_{db}+ \epsilon}}$ ， $\epsilon$确保除数不会是一个很小的数。由此，相对增大了横轴变化缩减了纵轴变化。

Adam optimization algorithm

1. 基于 backward 计算 $dW$ 和 $db$
2. $v_{dW} = \beta_1 v_{dW} + (1-\beta_1)dW$ $v_{db} = \beta_1 v_{db} +(1-\beta_1) db$ $S_{dW} = \beta_2 S_{dW} + (1-\beta_2) d^2W$ $S_{db} = \beta_2 S_{db} + (1-\beta_2) d^2b$
3. $v_{dW}^{correst} = v_{dW}/(1-\beta_1^t)$ $v_{db}^{correst} = v_{db}/(1-\beta_1^t)$ $S_{dW}^{correst} = S_{dW}/(1-\beta_2^t)$ $S_{db}^{correst} = S_{db}/(1-\beta_2^t)$
4. $W = W - \alpha \frac{v_{dW}^{correst}}{\sqrt{S_{dW}^{correst} + \epsilon}}$ $b = b - \alpha \frac{v_{db}^{correst}}{\sqrt{S_{db}^{correst} + \epsilon}}$
   在该算法中， $\beta_1$ 通常设为 $0.9$， $\beta_2$ 通常设为 $0.999$， $\epsilon$ 通常设为 $10^{-8}$， $\alpha$ 需要调节。

学习率衰减

原因

在运算初期，由于距离最优点较远，可以承受较大的学习率；在收敛过程中，学习率应慢慢衰减才能慢慢迭代到最优值处。

衰减方法

1. $\alpha = \frac{1}{1+ \text{decay}\_\text{rate}*\text{epoch}\_\text{num}} \alpha_0$
2. $\alpha = 0.95^{\text{epoch}\_\text{num}} \alpha_0$
3. $\alpha = \frac{k}{\sqrt{\text{epoch}\_\text{num}}} \alpha_0$或 $\alpha = \frac{k}{\sqrt{\text{mini}\_\text{batch}\_\text{num}}} \alpha_0$，这里 $k$ 为超参数。
4. 离散下降学习速率，随着mini_batch_num 的增大，逐渐减小。

局部最优点

当网络参数较多的情况下，优化过程中不易困在局部最优点。在局部最优处的函数平稳，学习速率较慢，此时可以通过优化方法来加快学习速率。