吴恩达深度学习总结(2)

回顾 Logistic Regression

$z = \omega^Tx + b \to a=\sigma(z) \to \mathcal{L}(a,y)$

浅层神经网络(只有一层隐藏单元)

在本周的课程中，浅层神经网络的 $W$ 均没有转置，也就是说，对于 $m$ 个大小为 $n_x$ 的输入样本， $W$ 的大小为 $m*n_x$

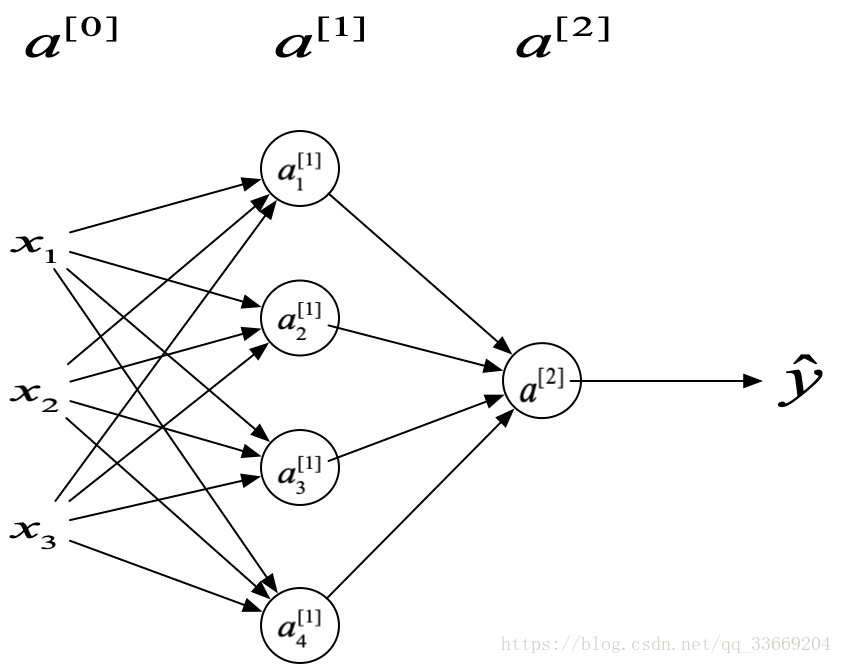
神经网络的命名中，输入层的下一层作为神经网络的第一层，输出层作为神经网络的最后一层。图中每一个节点进行线性和非线性变换，即 $z = \omega^Tx + b$ 和 $a = g(z)$， $g(x)$ 为激活函数。
要理解课程最重要的是分清每个符号的代表的意思

网络中每个符号的含义

以每个输入样本为照片拉成的向量为例，输入样本的大小为 $n_x * m$， $n_x = w*h*channels$
$x_i$：单个输入向量的 $i$ 位置上的值

$a^{[j]}$： 第j层的输入值

$a^{[j]}_i$： 第 $j$ 层的第 $i$个输入值

$n^{[i]}$：第 $i$ 层输入向量的维度， $n^{[0]} = n_x$

$x^{(i)}$：第 $i$ 个输入的样本

所以该浅层神经网络的第一层计算过程可以表示为
$z_1^{[1]} = \omega_1^{[1]T}x^{(i)} + b_1^{[1]}, a_1^{[1]} = g(z_1^{[1]})$
$z_2^{[1]} = \omega_2^{[1]T}x^{(i)} + b_2^{[1]}, a_2^{[1]} = g(z_2^{[1]})$
$z_3^{[1]} = \omega_3^{[1]T}x^{(i)} + b_3^{[1]}, a_3^{[1]} = g(z_3^{[1]})$
$z_4^{[1]} = \omega_4^{[1]T}x^{(i)} + b_4^{[1]}, a_4^{[1]} = g(z_4^{[1]})$
整个网络的计算过程可表示为
$Z^{[1]} = W^{[1]}A^{[0]} + b^{[1]}，A^{[0]}\in (n_0*m), W\in(n_1*n_0),b_1\in(n_1,1)$
$A^{[1]} = g(Z^{[1]})$
$Z^{[2]}=W^{[2]}A^{[1]} + b^{[2]}，A^{[1]}\in (n_1*m), W\in(n_2*n_1),b_1\in(n_2,1)$
$A^{[2]}=g(Z^{[2]})$
$W^{[1]}$ 的直观表示为
$\left[ \begin{matrix} —— & \omega^{[1]T}_1 & —— \\ —— & \omega^{[1]T}_2 & —— \\ —— & \omega^{[1]T}_3 & —— \end{matrix} \right]$

激活函数的选择

可选函数

$Sigmoid: a = \frac{1}{1+e^{-z}}$
$Tanh: a = \frac{e^{z} - e^{-z}}{e^{z}+e{-z}}$
$ReLU: a=\max(0,z)$
$leaky\;ReLU: a=\max(0.01z, z)$

激活函数的选择

$sigmoid$ 函数在二分类具有很好的表现性能；除了该场景 $tanh$ 函数几乎在其他所有场合比 $sigmoid$ 函数有更好的表现性能； $sigmoid$ 和 $tanh$ 通常只在输出层使用，其余层的激活函数通常选择 $ReLU$，因为 $sigmoid$ 或 $tanh$ 在 $z$ 较大或者较小时的梯度较小，使用梯度下降法速率变化较慢，而 $ReLU$ 在大多数 $z$ 空间内的激活函数的导数比0大很多，从而使梯度下降很快，当 $z < 0$ 时，尽管梯度为0，但只要隐藏单元足够多就可以保证训练的速率； $leaky\;ReLU$ 的表现性能略优于 $ReLU$，但没有很广泛的应用

使用非线性激活函数

如果使用线性激活函数，多个隐藏层的激活函数经线性变换后可以变为一个式子，多个隐藏层没有意义，因此只能使用非线性激活函数

神经网络的梯度下降

最后一层激活函数为 $sigmoid$ 函数
$dZ^{[2]}=A^{[2]}-Y$
$dW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T}$
$db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis = 1, keepdims = True)$
$dZ^{[1]}=W^{[2]T}dZ^{[2]}*g^{[1]'}(Z^{[1]})$
$dW^{[1]}=\frac{1}{m}dZ^{[1]}X^T$
$db^{[1]}=\frac{1}{m}np.sum(dZ^{[1]}, axis=1, keepdims=True)$
注意 $dZ^{[1]}$ 的求解是两个矩阵对应位置相乘，使用 $np.sum()$ 时注意 $keepdims$ 保证矩阵加法不会使矩阵维度减少，避免不必要的错误

梯度下降详解

$n^{[i]}$ 为每一个层的节点个数
$\mathcal{L}(A^{[2]},y) = \frac{1}{m}\sum_{i=1}^{m}J(A^{[2]},y)，\mathcal{L} \in(1*1)$
$J(A^{[2]},y)=-(y\log A^{[2]}+(1-y)\log(1-A^{[2]}))， J \in (1*m)$
$dA^{[2]}=-(\frac{y}{A^{[2]}}-\frac{1-y}{1-A^{[2]}})，dA^{[2]} \in (1*m)$
$dZ^{[2]}=(A^{[2]}*(1-A^{[2]})dA^{[2]}=A^{[2]}-Y，dZ^{[2]} \in (1*m)$
$dW^{[2]} = \frac{1}{m}dZ^{[2]}A^{[1]T} ，dW^{[2]} \in (1*n^{[1]})这里乘 \frac{1}{m} 是因为通过 m 个样本的求和求得dW^{[2]}$
$db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]}, axis =1, keepdims=True)，db^{[2]} \in (1*1)$
$dZ^{[1]} = W^{[2]T}dZ^{[2]}*g^{[1]'}(Z^{[1]})，dZ^{[1]} \in(n^{[1]}*m)，根据维度对比，这两个矩阵只能点乘$
$dW^{[1]} = \frac{1}{m}dZ^{[1]}X^T，dW^{[1]} \in(n^{[1]}，n^{[0]}$
$db^{[1]} = \frac{1}{m}np.sum(dZ^{[1]}, axis =1, keepdims = True)，db \in(n^{[1]},1)$
对矩阵求导，最好是根据输出矩阵的维度确定矩阵转置和相乘的位置

初始化

对logistic来说，可以将 $\omega$ 初始化为0；但对于浅层神经网络而言，如果将 $W$ 初始为0，那么两个节点完全对称，节点计算一样的函数，在迭代之后的计算仍然相同；也就是说无论如何迭代计算两个节点的权重都相同。
在实际应用时用 $np.random.randn(())*0.01$ 初始化 ,选择乘0.01是为了使 $W$ 变小，那么激活函数就不会落在函数平缓的地方，加快迭代速率。当训练浅层网络时，0.01满足要求，对于深层网络则需要选择其他的数值。