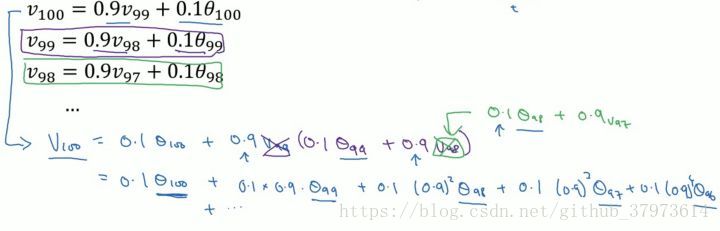1、mini-batch梯度下降法:
mini-batch size=m,就是我们平常用的梯度下降,即batch梯度下降
mini-batch size=1,则为随机梯度下降:每次迭代,只对一个样本进行梯度下降,大部分时间你向着全局最小值靠近,但有时候会远离最小值,因为那个样本恰好指的方向不对,因此随机下降是又很多噪声的。平均看来,它最终会靠近最小值,因为随机下降法永远不会收敛,而是会在最小值附近波动,不会达到最小值而停留。
m相对来说太大,1又太小,因此需要选择一个合适mini-batch尺寸,如果样本集少于2000,可以直接用batch梯度下降法;若样本集太大,一般可以用mini-batch尺寸为64~512(考虑到电脑内存设置和使用方式,用2的某次方会更好一些)
2、指数加权平均与指数加权平均的偏差修正
指数加权平均的关键函数:
vt是迭代得到的,最初令其为0,一步步迭代计算,但最后是一种平均数,我们用这种平均数来代替theta。可以认为我们由原来以往变化趋势乘以一个权重beta,和当下的变化乘以权重1-beta,这样可以两者之和表现出一部分现在的变化,同时也更表现出了以往的一种应该发展的趋势。
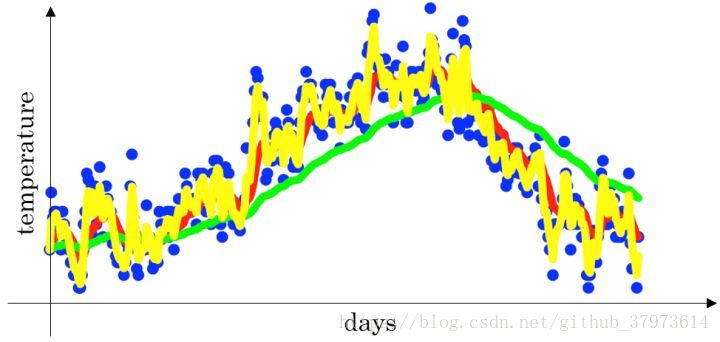
下面是一个关于温度和天气的散点图:
- 当
时,指数加权平均最后的结果如图中红色线所示;比较合适的趋势和上下波动
- 当
时,指数加权平均最后的结果如图中绿色线所示;因为
较小,所以更多的体现了前面一部分趋势
- 当
时,指数加权平均最后的结果如下图中黄色线所示;因为
较大,所以波动较大,体现了一个变化
指数加权平局数公式的好处之一:它只占用极少的内存,电脑内存只占一行数字而已,不断的覆盖就可以了。当然它不是最好的,也不是最精确的。如果要计算移动窗,可以直接计算过去10天或者50天的和,再除以10或者50就好,如此往往得到更好的估测。但缺点是,必须占用更多的内存,执行更加复杂。
来自吴恩达老师:
我们可以看到指数加权平均的求解过程实际上是一个递推的过程,那么这样就会有一个非常大的好处,每当我要求从0到某一时刻(n)的平均值的时候,我并不需要像普通求解平均值的作为,保留所有的时刻值,类和然后除以n。而是只需要保留0-(n-1)时刻的平均值和n时刻的温度值即可。也就是每次只需要保留常数值,然后进行运算即可,这对于深度学习中的海量数据来说,是一个很好的减少内存和空间的做法。
3、momentum梯度下降
momentum梯度下降总是会比标准的梯度下降要快。基本的想法是,计算梯度的指数加权平均数,并利用该梯度更新你的权重。
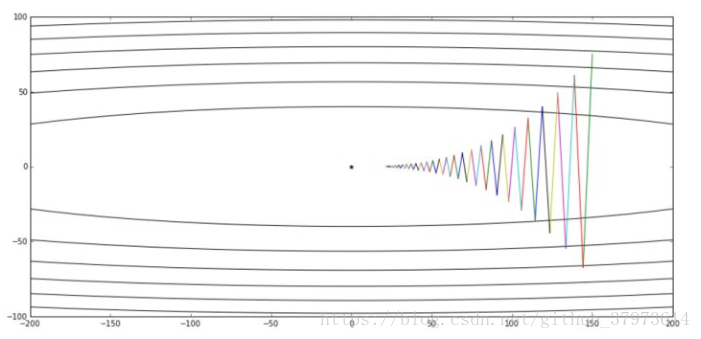
如下图:
这个图中,设初始点靠近横轴,远离纵轴,如果进行一次梯度下降的迭代,无论是batch还是mini-batch梯度下降法,都会计算很多步的迭代,在纵轴方向来回摆动很多次,慢慢的摆动到最小值。这种上下波动减慢了梯度下降法的速度,我们无法使用更大的学习率。因为如果使用了较大的学习率, 那么结果可能会偏离函数的范围。为了避免摆动过大,需要使用一个较小的学习率。
另一个角度来看:从纵轴上我们希望学习慢一点,而横轴上我们希望学习的快一点,希望在横轴上我们快速接近最小值点。所以使用momentum梯度下降,我们需要做的是,在每次迭代中,确切来说,是在第t次迭代中,我们会计算微分dw,db。用现有的mini-batch计算dw,db。
V_dW = β*V_dW + (1-β)*dW
V_db = β*V_db + (1-β)*db
更新参数:
W = W - α*V_dW
b = b - α*V_db
这样就可以减缓梯度下降的幅度了,在纵轴上摆动变小,在横轴上运动更快。
Momentum的一个本质,就是如果你要最小化碗状函数,他们能够最小化碗状函数,这些微分项(dW,db),想象它们是你从山上往下滚的一个球,提供了加速度,Momentum项(V_dW,V_db)就相当于速度。微分给了这个球一个加速度,此时球正往山下滚,球因为加速度越滚越快,因为β稍小于1,表现出一些摩擦力,所以球不会无限加速下去,所以【不像梯度下降法每一步都独立于之前的步骤】,你的球可以向下滚,获得动量,可以从碗向下加速,获得动量。
具体如何计算:
公式还是上面的四个公式,所以你有两个超参数,学习率α以及参数β。β控制着指数加权平均数,β最常用的值是0.9,即我们之前平均了过去十天的温度,所以在这里就是【平均了前十次迭代的梯度】,实际上,β为0.9时效果不错,你可以尝试不同的值,可以做一些超参数的研究,不过0.9是很棒的鲁棒数。
再来一个momentus梯度下降的解释:https://www.jianshu.com/p/58b3fe300ecb
4、RMSprop:root mean square prop
该算法也可以加速梯度下降。
这里假设参数b的梯度处于纵轴方向,参数w的梯度处于横轴方向(当然实际中是处于高维度的情况),利用RMSprop算法,可以减小某些维度梯度更新波动较大的情况,如图中蓝色线所示,使其梯度下降的速度变得更快,如图绿色线所示。
在如图所示的实现中,RMSprop将微分项进行平方,然后使用平方根进行梯度更新,同时为了确保算法不会除以0,平方根分母中在实际使用会加入一个很小的值如 。
5、Adam算法
Adam (Adaptive Moment Estimation)优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。
算法实现
- 初始化:
- 第
次迭代:
- Compute
on the current mini-batch
----- “Momentum”
----- “RMSprop”
----- 偏差修正
----- 偏差修正
- Compute
超参数的选择
:需要进行调试;
:常用缺省值为0.9,
的加权平均;
:推荐使用0.999,
的加权平均值;
:推荐使用
。
6、学习率衰减
实现:
- 常用:
- 指数衰减:
- 其他:
- 离散下降(不同阶段使用不同的学习速率)
7、局部最优
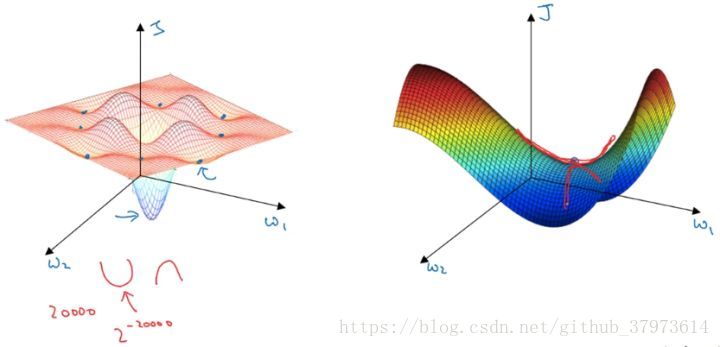
在低维度的情形下,我们可能会想象到一个Cost function 如左图所示,存在一些局部最小值点,在初始化参数的时候,如果初始值选取的不得当,会存在陷入局部最优点的可能性。
但是,如果我们建立一个高维度的神经网络。通常梯度为零的点,并不是如左图中的局部最优点,而是右图中的鞍点(叫鞍点是因为其形状像马鞍的形状)。
在一个具有高维度空间的函数中,如果梯度为0,那么在每个方向,Cost function可能是凸函数,也有可能是凹函数。但如果参数维度为2万维,想要得到局部最优解,那么所有维度均需要是凹函数,其概率为 ,可能性非常的小。也就是说,在低维度中的局部最优点的情况,并不适用于高维度,在梯度为0的点更有可能是鞍点,而不是局部最小值点。
在高纬度的情况下:
- 几乎不可能陷入局部最小值点;
- 处于鞍点的停滞区会减缓学习过程,利用如Adam等算法进行改善。