机器学习基石 Lecture2: Learning to Answer Yes/No

Perceptron Hypothesis Set

还是关注是否给客户发信用卡的问题。回顾上节中机器学习的流程，假设已知如下图中的一些客户信息，做出怎样的假设来得到假设集合 $H$呢？

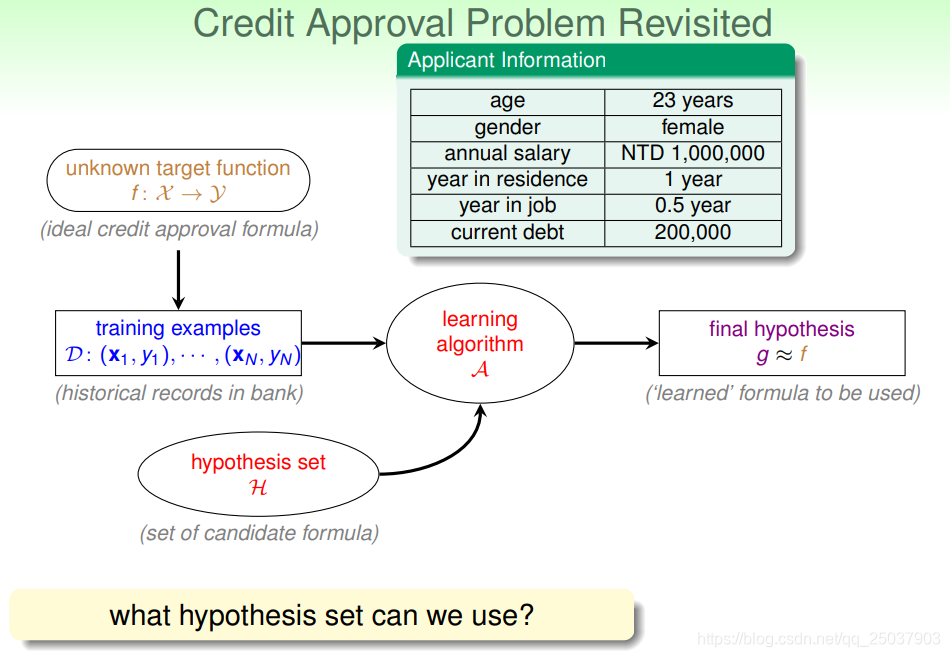
可以把客户信息写为一个向量 $x=(x_{1},x_{2},...,x_{d})$，每个维度都代表客户的一个特征。可以假设把这些特征维度进行加权求和来得到一个分数，如果这个分数超过某个阈值就下发信用卡，否则不下发。即假设h为：

这个假设就叫做感知机（perceptron）模型。

Perceptron Learning Algorithm

可以将上图等式中的阈值(threshold)也当做一个系数 $w_{0}$，对应第0个特征 $x_{0}=1$。则上述感知机模型可以写为向量内积的sign函数形式：

于是在二维平面上这个假设函数体现为一条线，一边被判断为+1（蓝色），另一边的点被判断为-1（红色）。而样本实际的y为+1时画为圈，-1时画为叉。

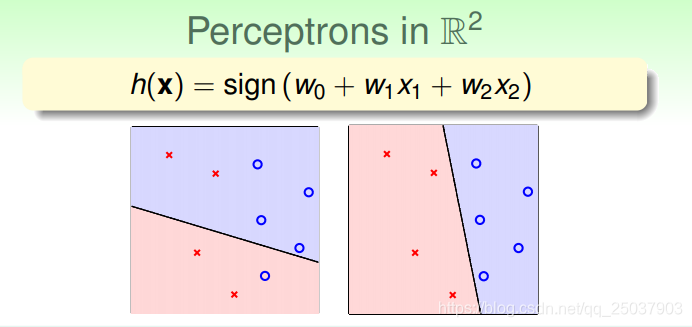
因此可以看出，感知机实际上是一个线性的二分类器。

有了假设空间 $H$，如何从中选出一个最接近实际函数 $f$的 $g$呢？可以根据在已有的数据集合上来判断。因为 $g$需要接近 $f$，因此在已有数据记录 $D$上， $g(x_{n})$的结果需要等于 $f(x_{n})$（必要不充分条件？）。

但是有个问题是假设空间 $H$是无穷大的，所以直接搜索比较困难。有一个想法是，从一个任意的函数 $g_{0}$开始，根据它在数据集 $D$的错误来不断改进自身。于是我们就有了感知机学习算法（Perceptron Learning Algorithm，PLA）：

1. 从任意一个参数为 $w_{0}$表示的函数 $g_{0}$开始，找到一个预测的结果和实际对应的 $y$值不同的样本。
2. 然后根据公式 $w_{t+1} \leftarrow w_{t}+y_{n(t)}x_{n(t)}$来对系数进行更新。
   直到找不到错误的样本为止，此时的参数 $w_{PLA}$对应的函数就是 $g$。

实际中算法第一步通常采用遍历数据集 $D$的方式，因此也叫作Cyclic PLA。

算法看起来很简单，但是还有一些遗留问题。比如：算法如何进行遍历样本？ 可以是普通遍历，随机遍历等。最后得到的算法 $g$是否真的约等于 $f$? 如果在 $D$上没有错误算法停止了，那么在 $D$上的效果肯定是近似相等的。但是在数据集 $D$之外的数据上表现如何呢？而且如果算法不停止更加无法知道 $g$是否与 $f$近似了。所以算法是否真的能够保证最终停止而不是无限循环呢？ 下面会给出算法确定会停止的证明。

Garrantee of PLA

如果存在一个对应的系数 $w$能够在数据集 $D$上不犯错误，也就是说 $D$中的样本能够被一条线性平面正确分隔开。我们说这样的 $D$具有线性可分性。

假设我们的数据集 $D$是线性可分的，那么是否PLA算法一定会停止呢？
线性可分的 $D$一定有一条不会犯错的分隔面对应的参数 $w_{f}$。

• 对于任意的样本都有 $y_{n(t)}w_{f}^{T}x_{n(t)} \geq min_{n}y_{n}w_{f}^{T}x_{n} > 0$.（因为每个样本都正确分类）
• $w_{f}$与 $w_{t}$的乘积为 $w_{f}^{T}w_{t+1} = w_{f}^{T}(w_{t}+y_{n(t)}x_{n(t)}) \\ \geq w_{f}^{T} + min_{n}y_{n}w_{f}^{T}x_{n} \\ > w_{f}^{T}w_{t}$
• 两者乘积在变大，但是需要证明并非是因为其长度增加而是夹角变小，这样才能说明我们的 $w_{t}$在靠近最好的分隔面对应的 $w_{f}$
• 计算 $w_{t}$的模。 $||w_{t+1}||^{2} = ||w_{t}+y_{n(t)}x_{n(t)}||^{2}\\= ||w_{t}||^{2}+2y_{n(t)}w_{t}^{T} x_{n(t)}+||y_{n(t)} x_{n(t)}||^{2}\\ \leq ||w_{t}||^{2} + 0 + ||y_{n(t)}x_{n(t)}||^{2}\\\leq||w_{t}||^{2}+max_{n}||y_{n}x_{n}||^{2}$因为我们是在分类错误的样本上进行更新，因此 $y_{n}w_{t}^{T}x_{n}\leq 0$。
• 根据以上几点，能够推出 $\dfrac{w_{f}^{T}}{||w_{f}||}\dfrac{w_{T}}{||w_{T}||} \geq \sqrt{T}*constant$。 过程如下： $\\ 1 \geq \dfrac{w_{f}^{T}}{||w_{f}||}\dfrac{w_{T}}{||w_{T}||} \\ \geq \dfrac{Tmin_{n}y_{n}w_{f}^{T}x_{n}}{||w_{T}|| ||w_{f}||}\\ \geq \dfrac{Tmin_{n}y_{n}w_{f}^{T}x_{n}}{\sqrt{Tmax_{n}||x_{n}||^{2}} ||w_{f}||} \\ \geq \sqrt{T}\dfrac{\rho}{R}$ $\\ 于是 T \leq \dfrac{R^{2}}{\rho^{2}}，因此算法一定在有限步骤内停止。$其中 $R^{2} = max_{n}||x_{n}||^{2}, \rho=min_{n}y_{n}\dfrac{w_{f}^{T}}{||w_{f}||}x_{n}$。都是常数。

因此，只要是数据集是线性可分而且不断地纠错，那么在PLA算法中：

• $w_{f}$和 $w_{t}$的内积快速增大，而 $w_{t}$的长度缓慢增大
• PLA算法得到的“线”会越来越接近 $w_{f}$，直到不犯错停止

PLA算法的优缺点：

• 优点：实现简单，运行速度快，在任意维度可行
• 缺点：1.需要假设样本线性可分。 2.不知道算法停止需要的时间。

Non-Separable Data

假设数据集中有一些噪音，这样就会导致数据集并不是完全线性可分的。这时候就需要进行一定的容错。对于PLA算法而言，可能从选择完全不犯错的分隔面变为选择一个犯错误最少的分隔面。

可以对PLA算法做一些简单的修改，先保有一条当前最好的分隔面，然后和先前一样进行更新。如果更新后的分隔面比当前最好更优，那么把当前最好换成这个更新后的分隔面，否则继续保有原来的。直到足够多的循环次数为止。