机器学习技法 Lecture2: Dual Support Vector Machine

Motivation of Dual SVM

首先回顾上节课讲的SVM，如果把其中的 $x_{n}$加上一个映射变换，就会得到以下形式的问题：

这样做能够得到一个带有非线性分隔面的结果。但是这样的方式会依赖于映射之后的假设空间的VC维，太大的话很难解。因此就想要得到一种不依赖于新的VC维的解法。

为了得到这个等价的SVM需要进行很多的数学推导，有时候也会直接用一些数学结论。这个等价的SVM是基于原始SVM的对偶问题的。

这里需要用到一个很关键的方法就是拉格朗日乘子法。这个方法在之前讲到的正则化里面也用到过。不过那里用到的时候是把系数 $\lambda$当做是一个已知的常数来解，因此用起来相对简单。但是在SVM的拉格朗日乘子法问题里是把 $\lambda$当做是一个变量来使用。不过在这里不用 $\lambda$来表示而是使用了 $\alpha_{n}$。又因为SVM里面有 $N$个限制条件，因此也会有 $N$个系数。于是我们得到新的SVM的形式为：

这样就把一个带约束问题转为一个无约束问题。新的问题里每一个系数 $\alpha_{n}$都大于0。而新的函数目标同样是最小化一个式子的结果，但是这个式子的结果与 $\alpha$的取值有关，因此最小化的是对于系数 $\alpha$最大化之后的结果。

而对于新的目标函数来说，有 $N$个项是对应原来的约束条件。当这些项遇到不满足条件的 $(b,w)$，项就是一个正值。而对 $\alpha$取max的结果就会是无穷大，因此不会取到这个对应的结果作为外层min的结果。于是最终的结果中，约束条件还是隐式被满足的。

Lagrange Dual SVM

首先如果把系数 $\alpha$固定，那么这个结果肯定是小于等于原来的目标函数的结果。

而对于这个固定了 $\alpha$的式子来说也有一个对于 $\alpha$的最大值，不过这个值还是会小于等于原来式子的结果。

不等式右边的问题就是这个问题的拉格朗日对偶问题。

在二次规划中，这种不等式形式的对偶问题叫做弱对偶形式。但是若对偶的二次规划问题，如果满足了一些条件，等式就能够成立。这些条件叫做constraint qualification。而这个SVM的拉格朗日对偶能够满足这些条件，因此存在一组解同时是不等式两边都得到最优解。

下面对这个对偶问题进行第一步的化简。首先看括号里min的部分。对于这个问题求最小，由于是个凸问题，所以最优解肯定是在梯度为0的位置。对b求导令导数为0。之后发现带着这个导数为0的约束可以将式子中的一项去掉而不影响结果。

第二步对 $w$进行求导，令导数为0同样得到一个约束。这个约束也可以化简目标函数：

而对于对偶问题的最优解，如果满足KKT条件，那么这个解也是原问题的最优解。其中KKT条件有四个部分：原问题可行性（primal feasible）、对偶问题可行性（dual feasibl）、对偶内部最优（dual-inner optimal）和原问题内部最优（primal-inner optimal）。

Solving Dual SVM

由上面的推导得到了SVM对偶问题的化简形式：

由于需要满足KKT条件，又多出了限制条件。不过这个问题最终是得到了一个像最初期望的那样，有N个变量和N+1个限制条件的问题，去掉了对于映射之后的维度的依赖。这个问题还是用二次规划来解决。

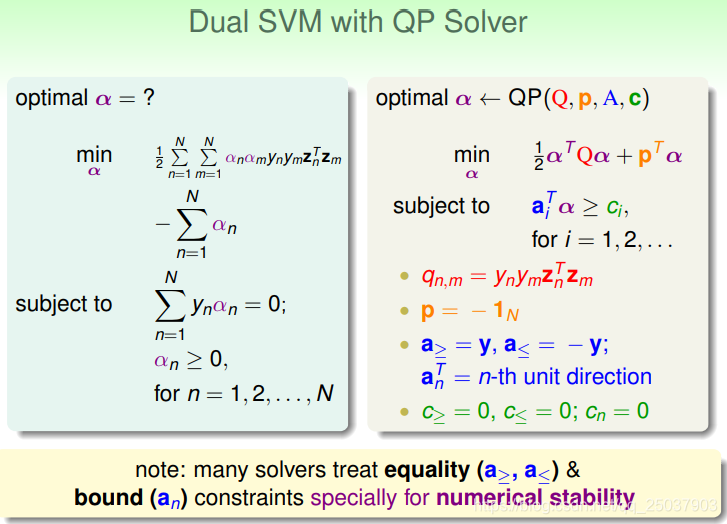
需要将等式约束写为两个不等式约束来满足二次规划的标准形式。

但是对于这样的二次规划依然存在一些问题。因为q一般是非0，因此Q矩阵是个密集的矩阵。如果N比较大，就会导致需要很大的存储空间。因此对于比较大的N有时候需要比较特殊的解二次规划的方法。

对于最终的结果，需要满足KKT条件。因此我们看到这四个不同的条件对应了不同的等式或不等式。而当我们得到了最优的 $\alpha$时，能够很轻松的根据等式得到最终的系数 $w$。

但是对于系数 $b$来说，。有两个限制条件。一个是primal feasible里限制的不等式 $y_{n}(w^{T}z_{n}+b)\geq 1$或者从另外一个primal-inner的等式限制中得到。 $\alpha_{n}(1-y_{n}(w^{T}z_{n}+b))=0$。而对于这个等式需要满足的是如果 $\alpha_{n}\geq 0$，那么对应的系数 $b=y_{n}-w^{T}z_{n}$。而满足这个条件的点都在距离分隔面最近的边界上，也就是support vector。只有满足 $\alpha_{n}\geq 0$的边界上的点才叫做support vector。

Messages behind Dual SVM

因此对于最终的结果来说，只有最靠近分隔面的点才会影响结果。而且对于 $\alpha_{n} \geq 0$的点叫做support vectors。也就是说在边界上的点包含了support vector的集合（因为边界上的点不一定满足 $\alpha_{n} \geq 0$，但不在边界上的点肯定不满足）。

因此对于结果来说，只需要计算support vectors的贡献即可：

于是SVM就是一个通过使用对偶最优的结果得到边界上的support vector最终得出一个有宽度的分隔面的算法。

其中w的结果是通过数据的计算来得到，这和PLA算法里的系数算法很像。对于这种结果我们叫做w ‘represented’ by data。而SVM里的w只通过支持向量来表示。

最后我们得到了两种形式的svm算法，一个是原始的SVM问题，一个是用对偶问题解的对偶型是。原始问题依赖于映射后的平面的维度，而对偶问题在N比较小时只依赖于变量数N。原始问题的物理意义是找到通过特定缩放限制的(w,b)，而对偶问题的物理意义是找到support vectors和他们对应的 $\alpha_{n}$。最终都得到一个线性分类器。

但实际上我们的工作并没有做完。因为我们的目标是拜托对于映射后的维度 $\widehat{d}$的依赖，但实际上在其中的内积运算时还是依赖于这个值。因此还有下一步的工作要做。