第三周 浅层神经网络
3.1 神经网络概览
将两个logistic分类器级联就可以得到一个非常简单的神经网络。
规定新的符号表示以区分不同层的中间变量\( z^{[l]}, W^{[l]}, b^{[l]} \),区别于样本的表示\( x^{(i)} \)
梳理一下:训练集中的每一个样本都要通过神经网络,计算最后输出和损失函数,所有样本的损失要进行累加,然后进行梯度反向传播,更新一次参数。这样的步骤要循环多次直到达到最优。
3.2 & 3.3 & 3.4 & 3.5 神经网络表示及计算
如图是一个最简单的神经网络,包括输入层、隐藏层和输出层,由于只有隐藏层和输出层包含参数,所以称为2层神经网络。
吴恩达机器学习课程在每一层额外增加了一个常数神经元,将其与下一层每个神经元的连接权重作为b,而本课程中b视为每个神经元中的一个单独参数,本质一样,表示不同。
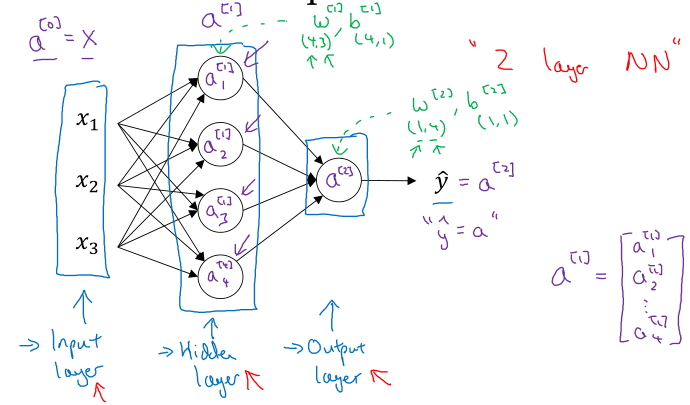
神经网络可以通过矩阵运算计算其输出,主要还是通过向量化实现。
将多个样本的特征向量组成样本矩阵,横向表示不同样本,纵向表示不同神经元,如:
\( Z^{[l]} = [ z^{[l](1)}, z^{[l](2)}, \dots, z^{[l](m)} ] \)
用吴恩达的话来说,进行矩阵乘积的时候,就是竖着扫一遍所有神经元 ,横着扫一遍所有样本。
3.6 & 3.7 & 3.8 激活函数
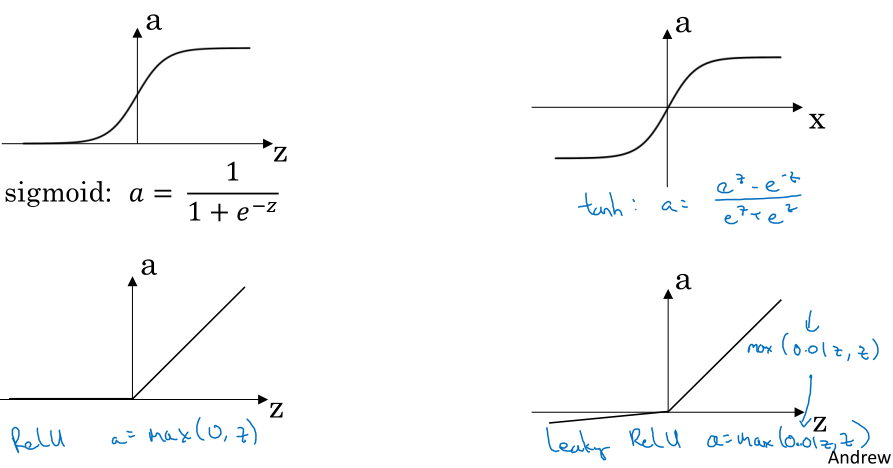
可选的激活函数包括:
- sigmoid函数: \( a = g(z) = \frac{1}{1+e^{-z}} \)
- tanh函数: \( a = g(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} \)
- ReLU: \( a = g(z) = max(0, z) \)
- Leaky ReLU: \( a = g(z) = max(0.01z, z) \)
sigmoid函数一般不再用在隐藏层,tanh函数的效果要更好,但在二分类问题中可以用在输出层;现在ReLU还是隐藏层最常用的激活函数,如果不知道如何选择激活函数,闭着眼睛选ReLU,它还有Leaky ReLU等变体,又引入了其他的参数。
为什么要用激活函数呢?没有激活函数的神经网络输出只是输入的线性加权,没有激活函数的隐藏层不如直接去掉隐藏层,没有激活函数的神经网络么得灵魂!
自己动手求一下上面激活函数的导数,或者...直接抄答案:
- sigmoid的导数:\( g'(z) = g(z)(1 - g(z)) \)
- tanh的导数:\( g'(z) = 1 - g^2(z) \)
- ReLU的导数:\( g'(z) = \begin{cases} 0 & \text{if } z < 0 \\ 1 & \text{if } z \ge 0 \end{cases} \)
- Leaky ReLU的导数:\( g'(z) = \begin{cases} 0.01 & \text{if } z < 0 \\ 1 & \text{if } z \ge 0 \end{cases} \)
其实后两个函数在\(z=0\)处并不可导,但是可以人为指定一个值,这并不影响最后结果。(概率论知识,一点的概率为0)
3.9 & 3.10 神经网络的梯度下降法
只有一个隐藏层的神经网络梯度反向传播公式:
\( \begin{aligned} dz^{[2]} &= a^{[2]} - y \\ dW^{[2]} &= dz^{[2]}a^{[1]^T} \\ db^{[2]} &= dz^{[2]} \\ dz^{[1]} &= W^{[2]^T}dz^{[2]} * g^{[1]'}(z^{[1]}) \\ dW^{[1]} &= dz^{[1]}x^T \\ db^{[1]} &= dz^{[1]} \end{aligned} \)
注意关于公式中\(dz\)等表述的意思在前一篇博客介绍过了,是代价函数对各中间变量的导数。梯度反向传播最重要的就是\(dz\)的计算与反向传播,在吴恩达机器学习课程中曾用\(\delta\)表示,其实就是代价函数对各层\(z\)变量的导数,\(z\)表示各层神经元中通过激活函数之前的变量。
在理解向量化公式时,关注矩阵的形状变化很有作用。
进一步,多样本的梯度反向传播:
\( \begin{aligned} dZ^{[2]} &= A^{[2]} - Y \\ dW^{[2]} &= \frac{1}{m}dZ^{[2]}A^{[1]^T} \\ db^{[2]} &= \frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True) \\ dZ^{[1]} &= W^{[2]^T}dZ^{[2]} * g^{[1]'}(Z^{[1]}) \\ dW^{[1]} &= \frac{1}{m}dZ^{[1]}X^T \\ db^{[1]} &= \frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True) \end{aligned} \)
3.11 随机初始化
如果神经网络的权重全部初始化为0,那么无论网络训练多久,每个神经元对应的权重都在进行同样的变化,即“对称”。所以初始化权重有两个最基本的原则:
- 随机初始化。
- 初始权重尽量小。防止梯度饱和,训练速度减慢。