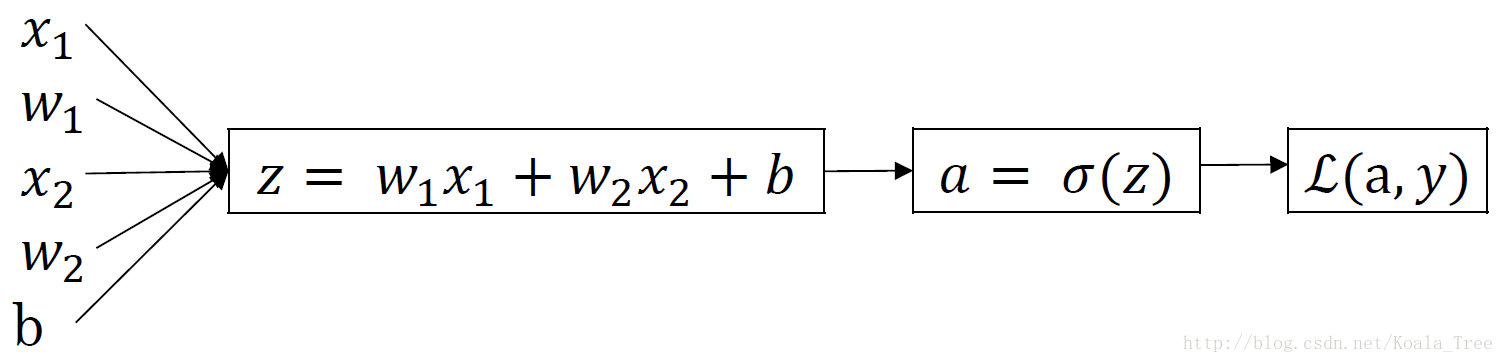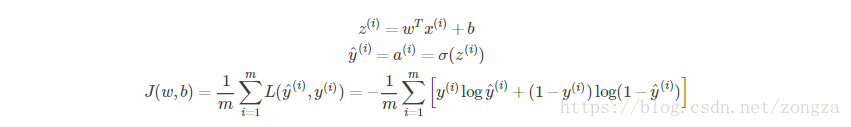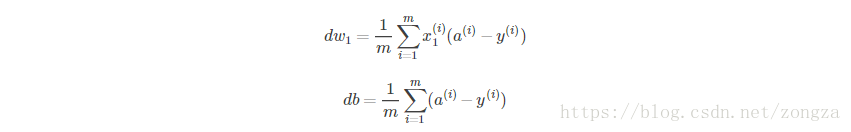吴恩达Coursera深度学习课程 course1-week2 总结

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/zongza/article/details/82832228

P0前言

• 第一门课 : Neural Networks and Deep Learning(神经网络和深度学习)
• 第二周 : Basics of Neural Network Programming(神经网络编程基础)
• 主要知识点 : logistic Regression(逻辑回归)、Cost Function(代价函数)、Gradient Descent(梯度下降)、Vectoriation(计算向量化)、Loss Function(损失函数) 等

视频地址: https://mooc.study.163.com/learn/2001281002?tid=2001392029#/learn/announce

P1总结

1.二分类问题

符号定义:

• x: 表示一个 $n_{x}$维数据,为输入数据,维度为( $n_{x}$,1)
• y: 表示输出结果,取值为{0,1}
• ( $x^{(i)}$, $y^{(i)}$): 表示第i组数据,一组数据包含输入值和对应的分类结果
• X=[ $x^{(1)}$, $x^{(2)}$,…, $x^{(m)}$]: 表示所有的训练数据集输入值,X.shape=( $n_{x}$,m)
• Y=[ $y^{(1)}$, $y^{(2)}$,…, $y^{(m)}$]: 对应表示所有训练数据集的输出值,Y.shape=(1,m)

注意:
X中的 $x^{(i)}$通常横向排列而不是纵向排列

2.逻辑回归

逻辑回归主要用来求条件概率,也就是在当前观测数据的前提下对数据所属类别的预测值 $\hat{y}=P(y=1|x)$:
$\hat{y}=w^{T}x+b$
上述公式就是逻辑回归的Hypothesis Function(假设函数)的主体.但是他还存在一些明显的不足:

1. 预测值是一个概率,概率必须在0和1之间,该公式显然不能使 $\hat{y}$满足这个条件
2. 此时 $\hat{y}$是关于x的线性函数,我们需要的是x和 $\hat{y}$保持非线性关系

为此,引入激活函数sigmoid(https://baike.baidu.com/item/Sigmoid函数/7981407?fr=aladdin),来解决上述两个问题,令:
$\hat{y}=Sigmoid(w^{T}x+b)=\sigma(z)$
其中:
$\sigma(z) = \frac{1}{1+e^{-z}}$

注意:
这里还存在一个梯度消失的问题,因为 $\sigma^{'}(z)= \sigma(z)(1-\sigma(z))$,所以有:
$\frac{d\hat{y}}{dz}= \sigma(z)(1-\sigma(z))$
上式最大值为0.25(对应z=0, $\sigma(z)=0.5$),也就是说梯度变化的最快速度也只有0.25,而随着参数更新,每次迭代更新后z会变大(更新目标是使预测概率 $\hat{y}$变大,其实也即是z变大),那么 $\sigma(z)$会变大,对应 $\sigma^{'}(z)$会变小,也就是说下一次迭代更新的步伐会越来越小,最终导致"梯度消失"

3.逻辑回归 的 损失函数

3.1.loss function

对参数的更新一般需要用到极大似然估计,为此需要找到似然函数(一般为某种条件概率),求参数的过程就是求给定条件下使得似然函数取最大值时的参数.

对于单一的样本数据(x,y),令逻辑回归的参数为w和b,那么他们的似然函数就是P(y|x),则有:
if y=1 then $P(y|x)=P(y=1|x)=\hat{y}$
if y=0 then $P(y|x)=P(y=0|x)=1-\hat{y}$
将上述两式子合并可得:
$P(y|x)=\hat{y}^{y}(1-\hat{y})^{1-y}$
再对上式进行log处理(log函数是单调函数，不会改变原函数的单调性)可得:
$log(P(y|x))=ylog(\hat{y})+(1-y)log(1-\hat{y})$
对于上面这个对数似然函数(也就是条件概率),我们自然是希望他越大越好(越大,此时参数的估计值越准确),如果对这个式子加一个负号,就转化成了单个样本的 loss function,由于负号的存在,我们则是希望他越小越好(这也符合"损失"的字面直觉,损失越小当然就越好了):
$L(\hat{y},y)=-ylog(\hat{y})- (1-y)log(1-\hat{y})$

3.2.cost function

如果将训练样本扩展到m个,也就是全部训练集的Loss function总和的平均值即为训练集的代价函数(Cost Function).
$J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)})$

4.梯度下降

我们的目标是要求得似然函数取最大值,也就是代价函数取最小值时的w和b.由于梯度是函数在点(w,b)处下降最快的方向,沿此方向更新w和b可以得到更小的函数值,一直到遇到全局最优解或者局部最优解.
更新公式如下所示:
$\omega:=\omega-\alpha\frac{\vartheta J(w,b)}{\vartheta w}$
$b:=b-\alpha\frac{\vartheta J(w,b)}{\vartheta b}$
在编程中一般采用dw和db来表示上述两个公式的分式部分.

9. 逻辑回归中的梯度下降(Logistic regression gradient descent)

9.1.单个样本

• 逻辑回归(正向传播):

$z=w^{T}x+b$
$\hat{y}=a=\sigma(z)$
$L(a,y)=-ylog(a)- (1-y)log(1-a)$

• 梯度下降(反向传播):

  
  

9.2.m个样本

• 逻辑回归:

• 梯度下降:

  Cost function 关于w和b的偏导数可以写成所有样本点偏导数和的平均形式：
  

11. 向量化（Vectorization）

主要利用numpy.dot实现矩阵运算,加速计算过程.下面针对m个样本的逻辑回归和梯度下降分别进行向量化
逻辑回归:

Z = numpy.dot(W.T,X) + b
A = sigmoid(Z)

梯度下降:

dZ  = A-Y
dW  = 1/m*numpy.dot(X,dZ.T)   
#相当于以行为单位,每行对应一个参数w,用到不同数据的第一个特征值是为了求平均
db  = 1/m*numpy.sum(dZ)

参数更新:

W-=a*dW
b-=a*db

其中:

• X : ( $n_{x}$,m)
• W: ( $n_{x}$,1)
• b: 常数
• Y: (1,m)
• Z: (1,m)
• A: (1,m)
• dW: ( $n_{x}$,1)
• db: 常数