图
**概念**图是一种较线性表和树更为复杂的数据结构。在图形中,结点之间的关系可以是任意的,图中任何两个数据元素之间都可能相交。
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
线性表、树和图的比较如下:
(1) 线性表中将数据元素叫元素,树中将数据元素叫结点,图中将数据元素称为顶点。
(2) 线性表中可以没有数据元素,称为空表。树中可以没有结点,称为空树。在图中,不允许没有顶点。在定义中,若V是顶点的集合,则强调了顶点集合V有穷非空。
(3) 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻的两层结点具有层次关系,而图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边表示,边集可以是空的。
图的术语定义:
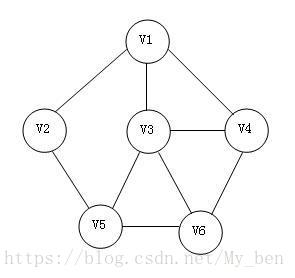
♢ 无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边,用无序偶对(Vi,Vj)表示。如果图中任意两个顶点之间的边都是无向的,则称该图为无向图。如下图所示:
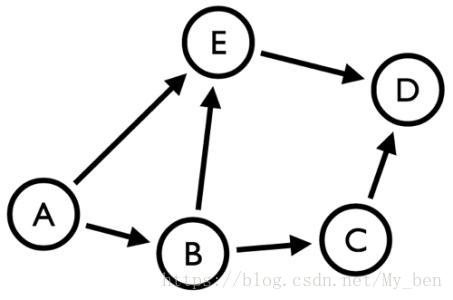
♢ 有向边:若从顶点Vi到Vj的边有方向,则称这条边为有向边,也成为弧。用有序偶(Vi,Vj)表示,Vi称为弧尾,Vj称为弧头。如果图中任意两个顶点之间的边都是有向边,则称该图为有向图。如下图所示:
♢ 简单图:在图中,若不存在顶点到自身的边,且同一条边不重复出现,称该图为简单图。
♢ 无向完全图:在无向图中,若任意两个顶点之间都存在边,称该图为无向完全图。含有n个顶点的无向完全图有(n(n-1)/2)条边。如下图所示:
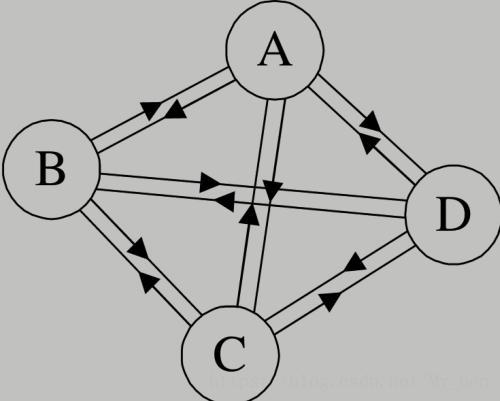
♢ 有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边,如下图所示:
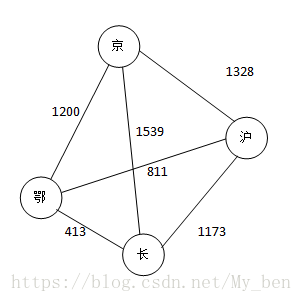
♢ 网:有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的树叫做权。这些权可以表示一个顶点到另一个顶点的距离或耗费。这种带权的图常称为网。如下图所示:
♢ 顶点的度是指关联该顶点的边的数目
♢ 子图是图的边(及边所关联的顶点)的子集所形成的图
♢ 图中的路径值得是一系列相邻顶点。简单路径是一条不包含重复顶点的路径。环路是起点和终点相同的路径。如果两盒顶点之间存在一条路径,则称这两个顶点是连通的。如果图中每对顶点之间都有路径相连,则称该图是连通图。如果一个图是非连通的,那么它是由一组连通分量组成。
图的表示
与其他抽象数据类型相似,为了对图进行操作,需要以某种有用的形式来表示图。基本上,有两种表示形式:邻接矩阵和邻接表
◆ 邻接矩阵表示
关于邻接矩阵,首先需要了解图数据结构的组成部分。图的表示需要顶点数、边数以及它们之间的连接关系。
本方法采用一个大小为V*V的矩阵Adj,其中矩阵的值为布尔值。如果存在一条从顶点u到顶点v的边,则设置Adj[u,v]为1,否则为0
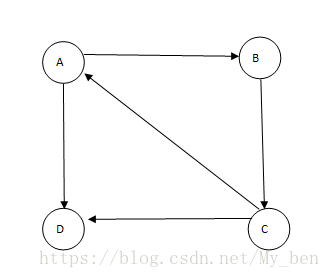
在矩阵中,无向图的每条边可以用两个二进制数来表示。即从一条边u到v的边用Adj[u,v]=1和Adj[v,u]=1表示。为了节省时间,只需要处理该对称矩阵的上三角矩阵的上三角或下三角元素。此外,假设每个顶点有一条连接其自身的边。所以,对于所有的顶点。Adj[u,v]都设置为1.如果图是有向图,那么仅需在邻接矩阵中标记一条边,如下图所示:
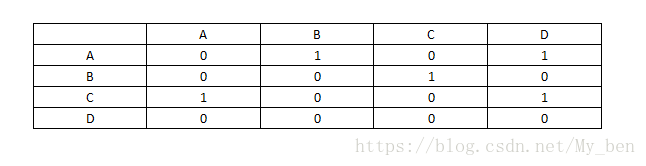
这个图的邻接矩阵可以表示为:
当图是稠密图时,邻接矩阵是一种很好的表示方式。邻接矩阵需要0(V2)个存储单位和0(V2)时间来初始化。如果边数和V2成正比,那么需要V2步来读取这些边。但如果图是稀疏的,那么初始化矩阵仍然需要0(V2)时间,并且初始化过程占据了整个算法的大部分运行时间。
用邻接矩阵表示图的主要代码如下:
public static void main(String args[]) throws IOException{
int arr[][]=new int[5][]; //声明矩阵arr
int i,j,tmpi,tmpj;
int [][] data={{1,2},{2,1},{2,3},{2,4},{4,3}}; //图形各边的起点值及终点值
for(i=0;i<5;i++) //把矩阵清零
for(j=0;j<5;j++)
arr[i][j]=0;
for(i=0;i<5;i++) //读取图形数据
for(j=0;j<5;j++){
tmpi=data[i][0]; //tmpi为起始顶点
tmpj=data[i][1]; //tmpj为终止顶点
arr[tmpi][tmpj]=1; //有边的点填入1
}
System.out.println("有向图形矩阵:\n");
for(i=1;i<5;i++)
{
for(j=1;j<5;j++)
System.out.println("["+arr[i][j]+"]"); //打印矩阵内容
System.out.println("\n");
}
}
◆ 邻接表表示
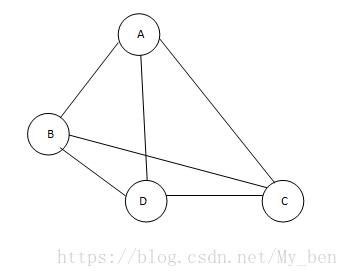
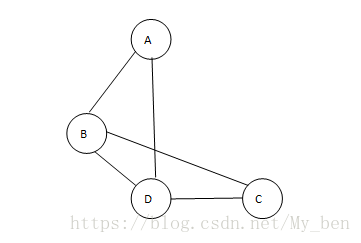
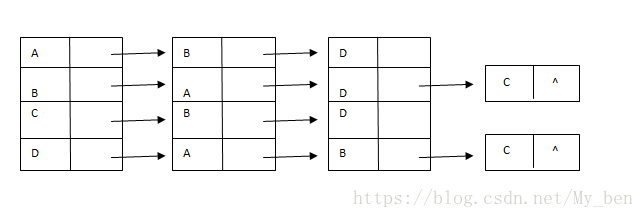
在这种表示方式中,所有与某个顶点v相连的顶点都在v的邻接表中列出,采用链表很容易实现,即邻接表中的每一个顶点v都有一个与其对应的链表,链表结点表示v的邻接点与v之间连接。链表的总数等于图中的顶点数。如下图所示,由于顶点A与B和D有边相连,所以将B与D添加到A的邻接表中。其他顶点的邻接表也类似。
对于邻接表的表示方式边的读入顺序也很重要。因为边的顺序决定了顶点在邻接表中的顺序。相同的图在邻接表中可以有许多不同的表示方式。边在邻接表中出现的顺序也会影响算法处理边的顺序。
用邻接表表示图的主要代码如下:
class Node
{
int x;
Node next;
public Node(int x)
{
this.x=x;
this.next=null;
}
}
class GraphLink
{
public Node first;
public Node last;
public boolean isEmpty()
{
retrun first=null;
}
public void print()
{
Node current=frist;
while(current!=null)
{
System.out.println("["+current.x+"]");
current=current.next;
}
System.out/println();
}
public void insert(int x)
{
Node newNode=new Node(x);
if(this.isEmpty())
{
first=newNode;
last=newNode;
}
else
{
last.next=newNode;
last=newNode;
}
}
}
public static void main(String args[]) throws IOException
{
int Data[][]= //图形数组声明
{{1,2},{2,1},{1,5},{5,1},{2,3},{3,2},{2,4},
{4,2},{3,4},{4,3},{3,5},{5,3},{4,5},{5,4}};
int DataNum;
int i,j;
System.out.println("图形(a)的邻接表内容:");
GraphLink Head[]=new GraphLink[6];
for(i=1;i<6;i++)
{
Head[i]=new GraphLink();
System.out.println("顶点"+i+"=>");
for(j=0;j<14;j++)
{
if(Data[j][0]==i)
{
DataNum=Data[j][1];
Head[i].insert(DataNum);
}
}
Head[i].print();
}
}
邻接表的缺点:使用邻接表表示方法无法有效的完全某些操作。以删除某个结点为例,在邻接表中,如果直接从邻接表中删除该结点,是可以做到的。然而,在邻接表中当该结点和其他结点有边相连时,则必须搜索其他结点对应的链表来删除该结点。尽管可以通过在两个表结点之间建立一条特殊的边,使得邻接表变为双向链表来解决此问题,但是处理这些额外的链接是有风险的。
图的遍历及算法
▷ 图的遍历
Ⅰ 深度优先搜索
为了解决有关图的问题,需要一种机制来遍历图。图的遍历算法也叫作图的搜索算法。与树遍历算法一样,图搜索算法也可以看作从某个源点开始,通过遍历边和标记顶点来搜索图。两种遍历图的算法为深度优先搜索(DFS)、广度优先搜索(BFS)。
深度优先搜索(DFS)算法的原理类似于树的前序遍历,本质上也使用栈来实现。对大多数算法,用布尔值足以区分未访问过/访问过得结点。
初始时所有顶点都被标记为未被访问过。DFS算法是从图中一个顶点u开始,首先考虑从u到其他顶点的边。如果该边通往一个已经被访问过的顶点,那么回溯到当前顶点u。如果该边通往一个未被访问过的顶点,则到达该顶点,并从该顶点开始访问,即将新的顶点变成当前顶点。重复这个过程直到算法到达“末端”。然后从这个“末端”点开始回溯。当回溯到起始顶点时,整个过程结束。
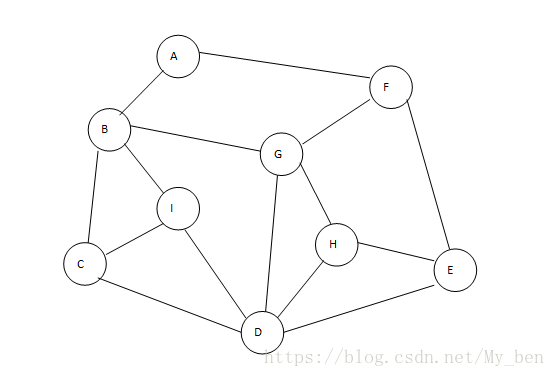
以下图为例:有时边会通往一个已经被访问过的顶点。这些边称为回退边,其余的边称为树边,因为从图中删除回退边会产生一棵树,最终产生的树称为DFS树,顶点的访问顺序称为顶点的DFS编号。
如果使用邻接表来表示图,则DFS算法的时间复杂度为0(V+E)。这是因为从某个顶点开始,算法只访问该顶点尚未被访问到的邻接点。同理,如果用邻接矩阵来表示图,那么算法难以快速找到所有与某个顶点相邻的边,此时的时间复杂度为0(V2)。
在上图中,访问先从A顶点开始,将A标记为已读。面前有两条路,通向B和F,我们给其定一个原则,在没有碰到重复顶点的情况下,始终向右边走。于是,我们走到了B顶点。这是面向C、I、G,遵循原则,这是走到了C顶点。然后一直顺着右手通道走,C=>D=>E=>F,这时我们走到了F顶点。如果一直遵守右手通行原则,最终会回到顶点A,因为A顶点一标记为已读,表示已经走过。此时,我们退回顶点F,走向G顶点,这时发现B、D已走过,于是走到H,但是我们会发现,D、E顶点我们都已走过。
此时我们是否已经遍历了所有顶点了呢?没有。可能还有很多分支顶点没有走到,所以我们原路返回,在顶点H处,所有通道已走完,返回到G,也无未走过通道,返回到F,没有通道,返回到E,有一条通往H的通道,但也是走过的,再返回到D,此时还有新顶点I没有标记,标记为已走过。继续返回,只带返回顶点A,确认已完成遍历任务,找到了所有的9个顶点。
深度优先的主要代码如下:
public static int run[]=new int[9];
public static GraphLink Head=new GraphLink[9];
public static void dfs(int current) //深度优先遍历子程序
{
run[current]=1;
System.out.println("["+current+"]");
while((Head[current].first)!=null)
{
if(run[Head[current].first.x]==0) //如果顶点尚未遍历,就进行dfs的递归调用
dfs(Head[current].first.x);
Head[current].first=Head[current].first.next;
}
}
public static void main(String args[])
{
int Data[][]= //图形边线数组声明
{ {1,2},{2,1},{1,3},{3,1},{2,4},{4,2},{2,5},{5,2},{3,6},{6,3},
{3,7},{7,3},{4,5},{5,4},{6,7},{7,6},{5,8},{8,5},{6,8},{8,6} };
int DtatNum;
int i,j;
System.out.println("图形的邻接表内容:"); //打印图形的邻接表内容
for(i=1;i<9;i++) //共有8个顶点
{
run[i]=0;
Head[i]=new GraphLink();
System.out.println("顶点"+i+"=>");
for(j=0;j<20;j++) //20条边线
{
if(Data[j][0]==1) //如果起点和列表的头相等,则把顶点加入列表
{
DataNum=Data[j][1];
Head[i].insert(DataNum);
}
}
Head[i].print(); //打印图形的邻接表内容
}
System.out.println("深度优先遍历顶点:");
dfs(1);
System.out.println("");
}
Ⅱ 广度优先搜索
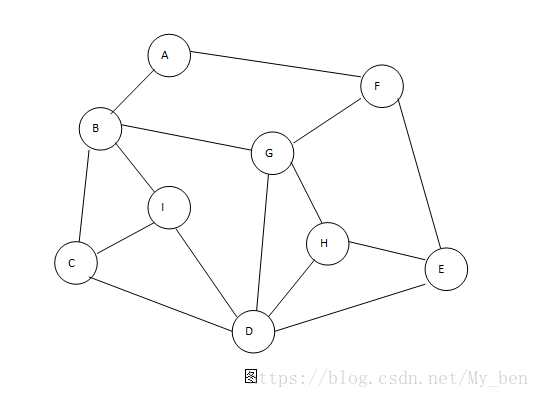
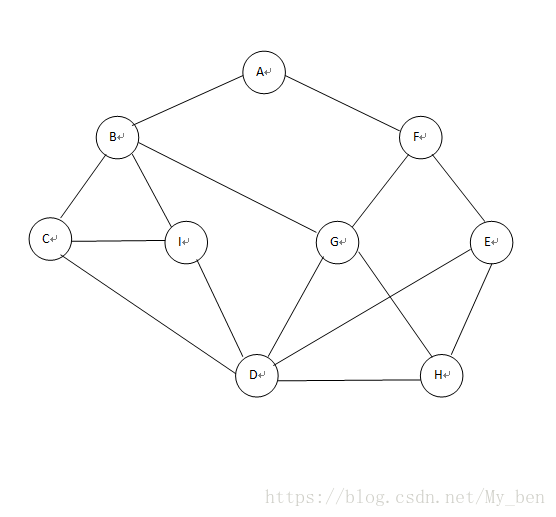
如果说图的深度优先遍历类似于树的前序遍历,那么图的广度优先遍历就类似于树的层序遍历。我们将下面的第一幅图稍微变形,变形原则是顶点A放置在最上面一层,如下面的第二幅所示。此时,在视觉上感觉图的形状发生了变化,其实顶点和边的关系还是完全相同的。
广度优先搜索(BFS)算法的原理类似于树的层次遍历,并且算法也使用了队列。事实上,层次遍历也是受到了BFS的启发。BFS逐层对图进行遍历。初始时,BFS从一个给定的顶点出发,该顶点位于0层,再逐步访问各层的顶点。
BFS算法重复这个过程,直至图的所有层都访问一遍。通常,BFS算法使用队列来存储,每一层的顶点。与DFS类似,假设初始时所有顶点都标记为未被访问过。已经处理过并从队列中移除的顶点标记为已访问过。利用另一个队列来表示所有已被访问的结点的集合,该队列将记录结点第一次被访问的顺序。
广度优先的主要代码如下:
public static int run[]=new int[9]; //用来记录各顶点是否遍历过
public static GraphLink Head[]=new GraphLink[9];
public final static int MAXSIZE=10; //定义队列的最大容量
static int[] front=1; //指向队列的前端
static int rear=-1; //指向队列的后端
//队列数据的存入
public static void enqueue(int value)
{
if(rear>=MAXSIZE) return;
rear++;
queue[rear]=value;
}
//队列数据的取出
public static int dequeue()
{
if(front==rear) return -1;
front++;
return queue[front];
}
//广度优先搜索法
public static void bfs(int current)
{
Node tempnode; //临时的结点指针
enqueue(current); //将第一个顶点存入队列
run[current]=1; //将遍历过的顶点设定为1
System.out.println("["+current+"]"); //打印该遍历过的顶点
while(front!=rear) //判断是否是空队列
{
current=dequeue(); //将顶点从队列中取出
tempnode=Head[current].frist; //先记录目前顶点的位置
while(tempnode!=null)
{
if(run[tempnode.x]==0)
{
enqueue(tempnode.x);
run[tempnode.x]=1; //记录已遍历过
System.out.println("["+tempnode.x+"]");
}
tempnode=tempnode.next;
}
}
}
Ⅲ DFS 和 BFS 的比较
对比 DFS 和 BFS 可知,DFS 的最大优势在于它的内存开销要远远小于 BFS,因为它不需要存储每一层结点的所有孩子结点指针。根据数据和查找内容的不同, DFS 和 BFS 各有优势。例如,在一个家族树中,需要查找某个人是否仍然健在且假设这个人处于树的末端,那么 DFS 是一个更好的选择,而 BFS 可能需要花费非常长的时间达到最后一层。
DFS 算法能更快的找到目标。现在,如果要寻找一个已经过世很长时间的人,那么这个人可能更接近树的顶端。在这种情况下,BFS 查找比 DFS快。因此,每种算法的优势取决于数据和要查找的内容。
不过如果图顶点和边非常多,不能在短时间内遍历完成,遍历的目的是为了寻找合适的顶点,那么选择哪种遍历就要仔细研究了。深度优先更适合目标比较明确,已找到目标为主要目的的情况,而广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。
▷ 最小生成树算法
Ⅰ 普里姆(Prim)算法
问题1:有一块木板,板上钉了一些钉子,这些钉子可以由一些细绳连接起来。如果每个钉子可以通过一根或者多根细绳连接起来,那么如何用最少的细绳把所有的钉子连接起来?
问题2:在某地分布着N个村庄,现在需要在N个村庄之间修路,每个村庄之间的距离不同,问怎么修才能使路程最短,事各个村庄连接起来。
以上问题都可以归纳为最小生成树的问题,用正式的表述方法描述为:给定一个无方向的带权图G=(V,E),最小生成树的集合T,T是以最小代价连接V中所有顶点互相连接的边E的权值最小集合。集合T中的边能够形成一棵树,这是因为每个结点(除了根结点)都能向上找到一个父结点。解决最小生成树问题已经有前人做过相关的研究,Prim(普里姆)算法和Kruskal(克鲁斯卡尔)算法,分别从点和边下手解决了该问题。
Prim算法简介:普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
Prim算法从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪心算法(后期会详细介绍)。
算法描述如下:
- 在一个加权连通图中,顶点集合V,边集合为E。
- 任意选中一个点作为初始顶点,标记为visit,计算所有与之连接的点的距离,选择距离最短的,标记为visit。
- 重复以下操作,知道所有点都被标记为visit:在剩下的点中,计算与已标记visit点距离最小的点,标记visit,证明加入了最小生成树。
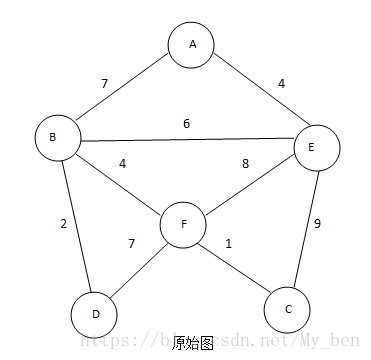
最小生成树的过程如下:
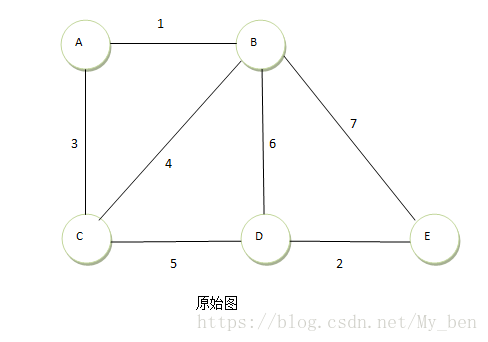
① 起初,从顶点A开始生成最小生成树,如下图所示:
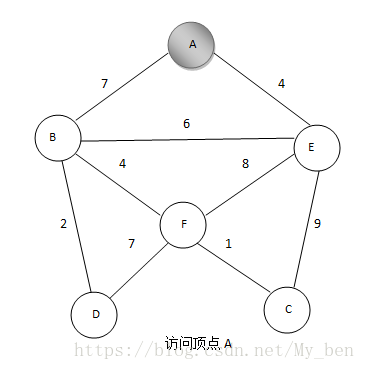
② 选择顶点A后,顶点置成visit,计算周围与它连接的点的距离。如下图所示:
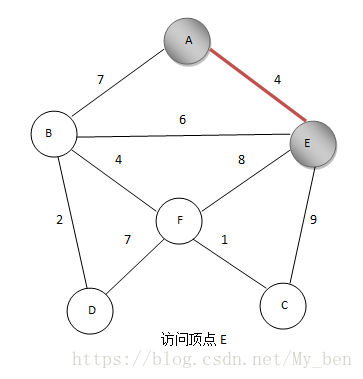
③ 与之相连的点距离分别为7、6、4,选择E点的距离最短,标记E,同时将AE边加入最小生成树,如下图所示:
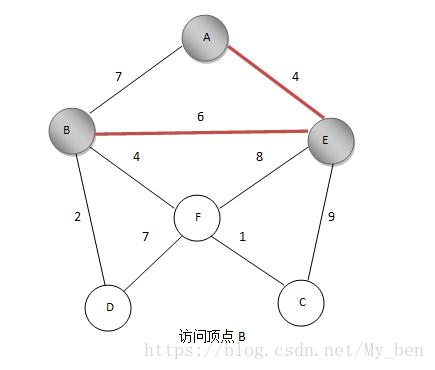
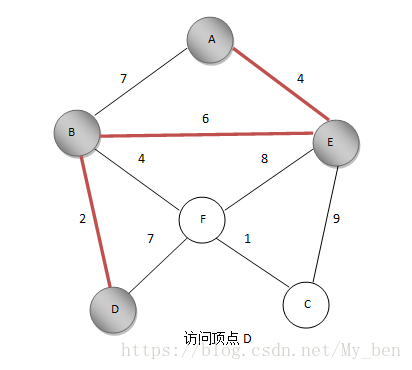
④ 计算与A、E相连的点的距离(已经标记的点不算),因为与A相连的已经计算过了,只需要计算与E相连的点,如果一个点与A、E都相连,那么它与A之间的距离之前已算过,如果它与E的距离更近,则更新距离值,这里计算的是未标记的点距离标记的点的最近距离,B、A之间距离为7,B、E之间距离为6,更新B和已访问的点集距离为6,而EF、EC的距离分别为8,9,所以还是标记B,将BE边加入最小生成树。如下图所示:
⑤ DB之间距离最短,标记D点,将BD边加入最小生成树。如下图所示:
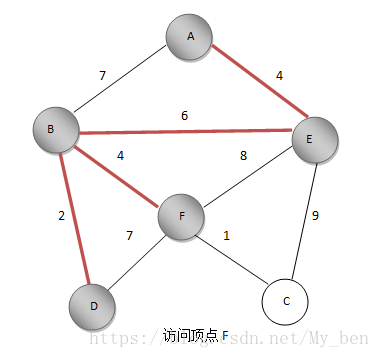
⑥ FD之前距离为7,FB之间距离为4,更新F的最短距离值为4,标记F,将BF边加入最小生成树。如下图所示:
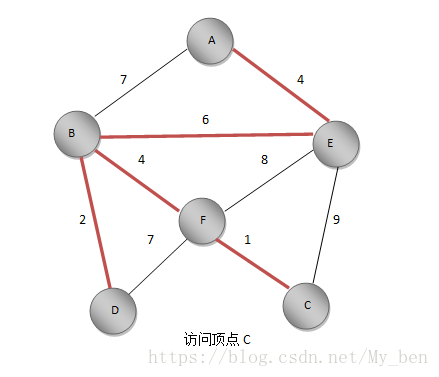
⑦ EC距离为9,FC距离为1,更新C点的最短距离值为1,标记C,将FC加入最小生成树。如下图所示:
Ⅱ 克鲁斯卡尔(Kruskal)算法
Kruskal是另一种计算最小生成树的算法,其算法原理如下:首先,将每个顶点放入其自身的数据集合中。然后,按照权值得升序来选择边,当选择每条边时,判断定义边的顶点是否在不同的数据集中。如果是,将此边插入最小生成树的集合中,同时,将集合中包含每个顶点的联合体取出;如果不是,就移动到下一条边。重复这个过程,直到所有的的边都探查过。
通过一组图式来变现算法的过程如下:
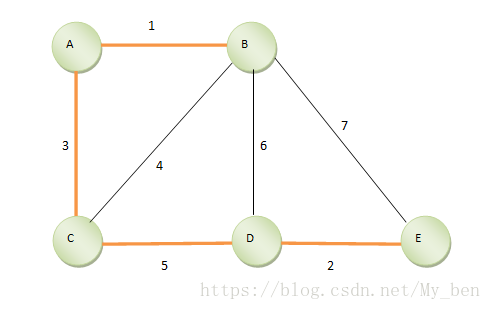
① 初始情况,一个联通图,定义针对边的数据结构,包括七点。终点和边长度。如下图所示:
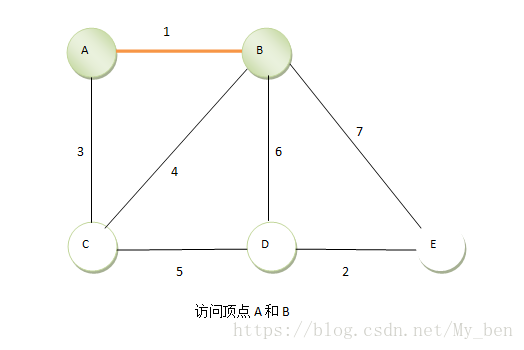
② 首先找到第一短的边AB,将AB放入到一个集合中,如下图所示:
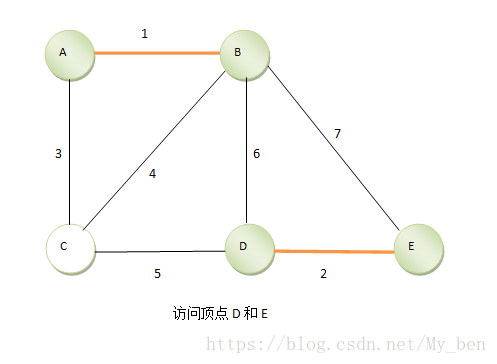
③ 继续找到第二短的边DE,将DE放入到一个集合中,如下图所示:
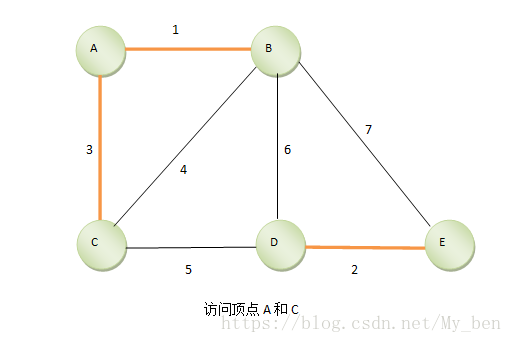
④ 继续找,找到第三短的边AC,因为A、B已经在一个集合里,再将C加入,如下图所示:
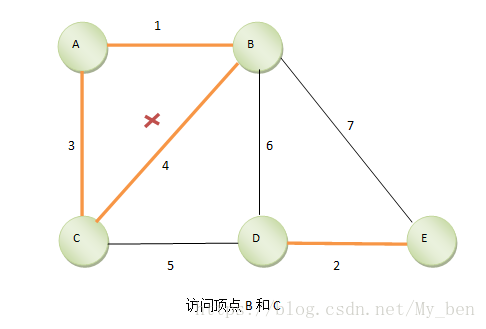
⑤ 继续找,找到B、C,因为B、C已经同属于一个集合,连起来的话就形成了环,所以边B、C不加入最小生成树。如下图所示:
⑥ 继续搜索,找到CD,因为D、E是一个集合的,B、A、C是一个集合,所以再合并这两个集合,如下图所示:
这样所有的点都归到了一个集合里,生成了最小生成树。