1.换元积分法包括第一类换元积分和第二类换元积分
2.深入理解换元积分法推导的前因后果以及公式应用
上一篇我们介绍了基本的不定积分公式,以及利用不定积分的线性性质求解稍微复杂的式子。今天我们继续介绍别的方法——换元积分法。
1
第一类换元积分法
换元积分法有两类,先介绍第一类换元积分法:

这里的证明是严格的,但是我们也有另外一种证明,它在逻辑上是不通的,但是在应用上是可以的,为什么这么说的,我们先来看证明:
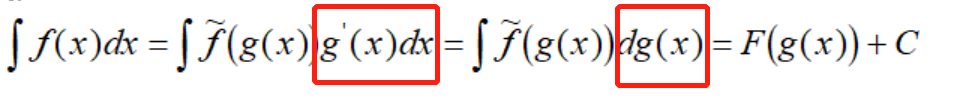
第一眼看起来,这个证明“天衣无缝”,红色部分利用了g(x)的微分,但这里之所以可以写成g(x)的微分,是因为不定积分被定义成了含有微分"dx"的形式:
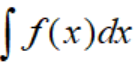
既然是定义,如果换另外一种定义呢,比如不带微分形式的定义:
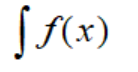
那么显然红色部分不再成立。
所以,科学家定义不定积分形式时,带微分”dx"是为了能够用第二种“因果倒置”的证明方式进行方便计算而“故意为之”。这一点格外重要,以后我们计算可以直接利用微分形式,但要注意,这不是原因,而是结果,真正的原因是第一种严格的证明.
从形式来看,微分部分就是凑出来的,因此,第一类换元积分法又被称为“凑微分法”。我们下面举几个例子.
例1
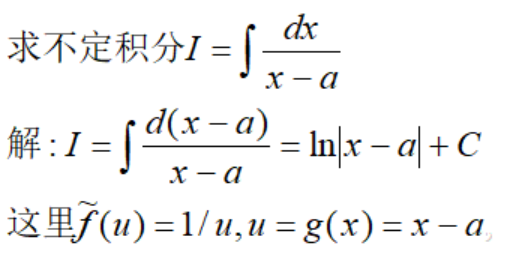
例2
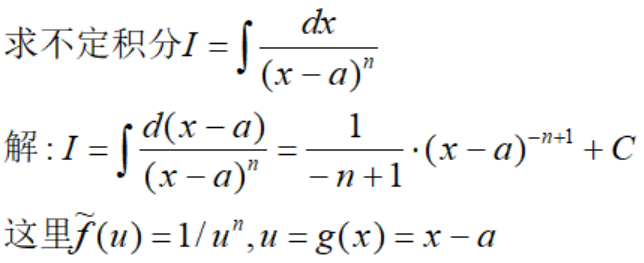
例3
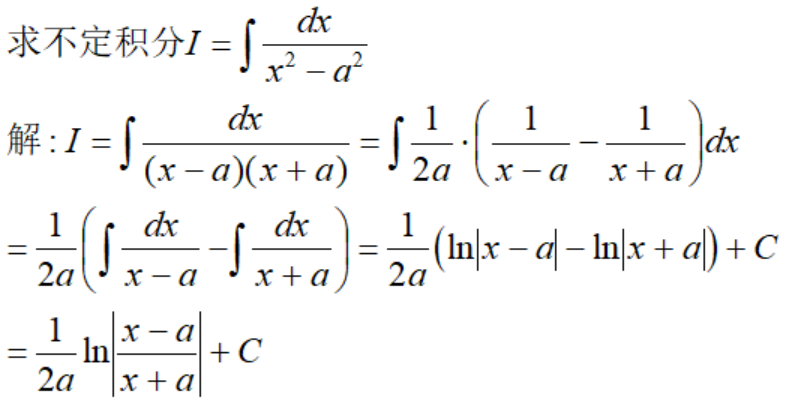
例4
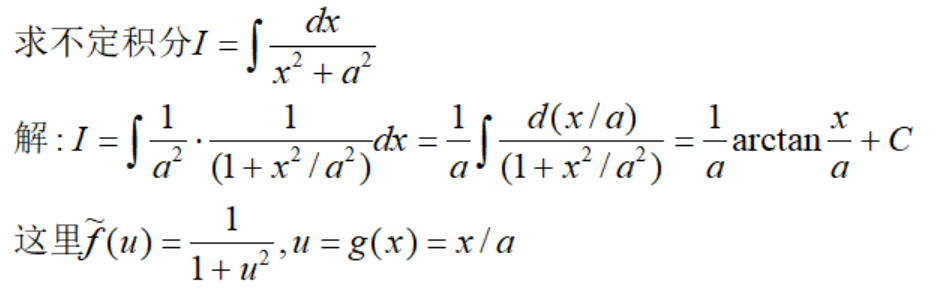
例5
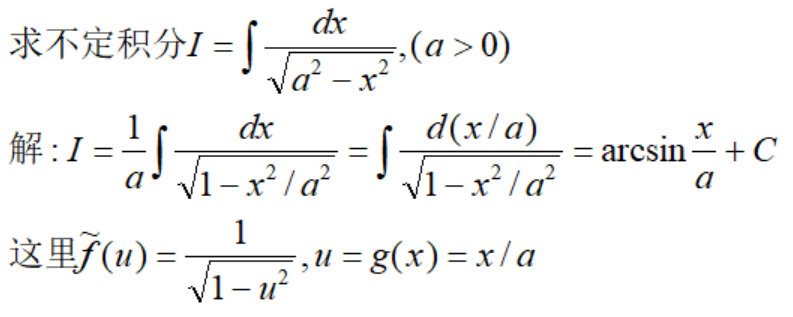
2
第二类换元积分法
接着我们介绍第二类换元积分法:
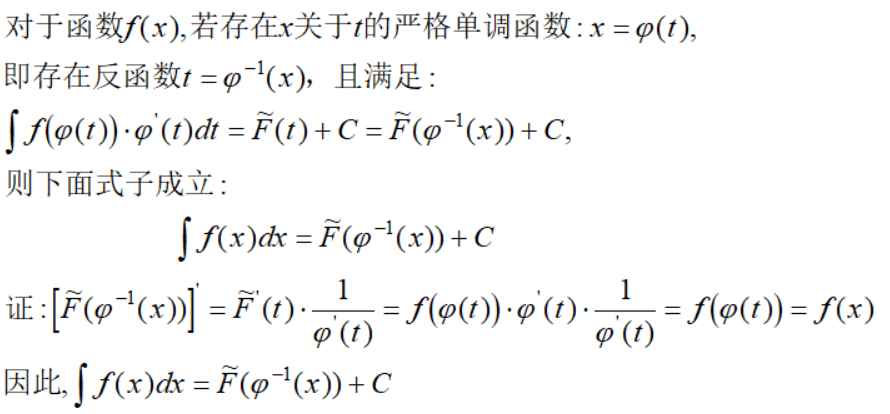
同理,下面等式成立:
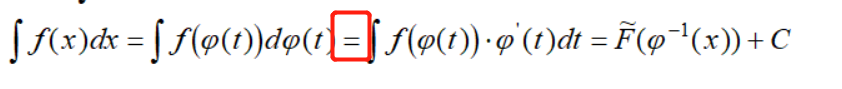
这与第一类换元积分类似,红色框的等号成立的原因是因为等式终端两边相等,科学家“故意”将不定积分记号带微分形式。这一点多次强调,要清楚其中的因果关系。
下面我们举几个例子加深对第二类换元积分的理解。
例6
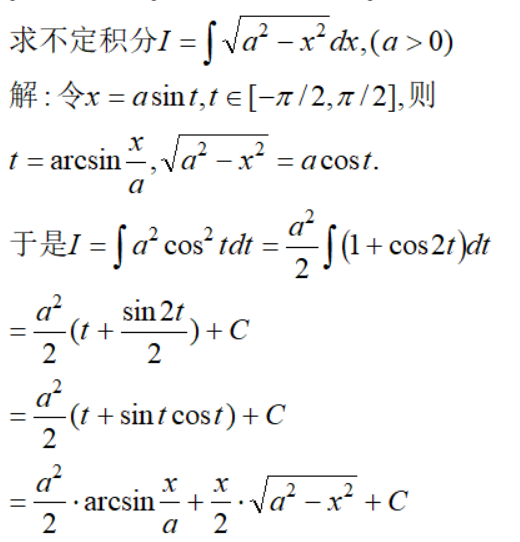
例7
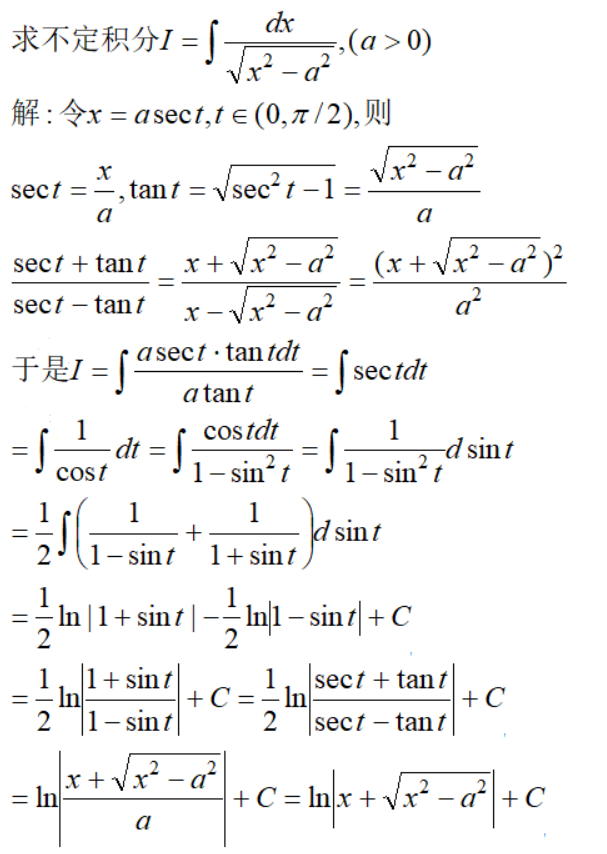
这里要注意的一个地方,就是x的取值只有大于a的情况,很显然,少考虑了x小于-a的情况,即:
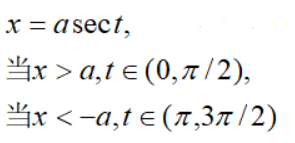
我们知道,对原函数求导时,我们并不会考虑x是否大于a还是小于-a,因此对于求不定积分的另外一种情况,答案肯定是一样的,因此我们考虑一种情形即可.