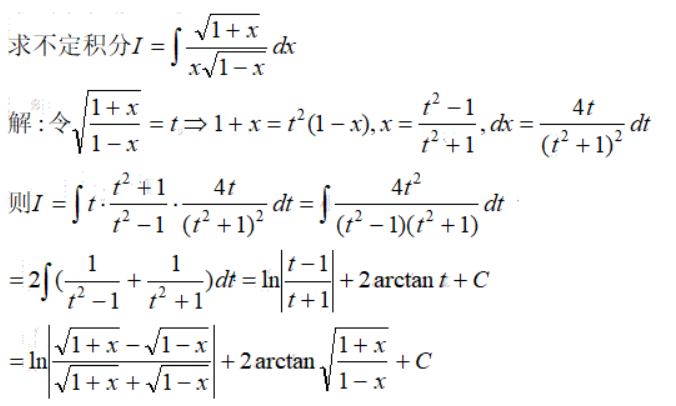1.初等函数的不定积分不一定是初等函数
2.有理函数的不定积分一定是初等函数,可以被积出来
3.部分无理函数通过变量代换可以转化为有理函数
至此,我们可以利用线性性质、换元积分和分部积分方法求解不定积分,但并非所有的不定积分都能被求解。比如下面的不定积分就无法求解:
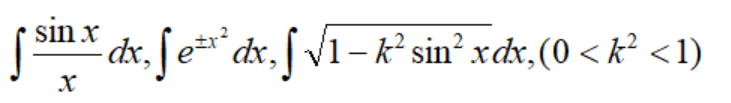
自然而然的,我们想要研究什么形式的不定积分是可以求解的。我们知道,不定积分和求导是互为逆运算,因为基本初等函数导数都是可求的,而初等函数是基本初等函数经过有限次的四则运算和复合运算得到,因此初等函数也是可以求导的:

我们要找到,F(x)是什么样的初等函数,它的不定积分可以求出来。
1
有理函数的不定积分可以求解,主要有下面的定理:

首先我们对有理函数R(x)的分母部分q(x)进行分析,由代数基本定理:
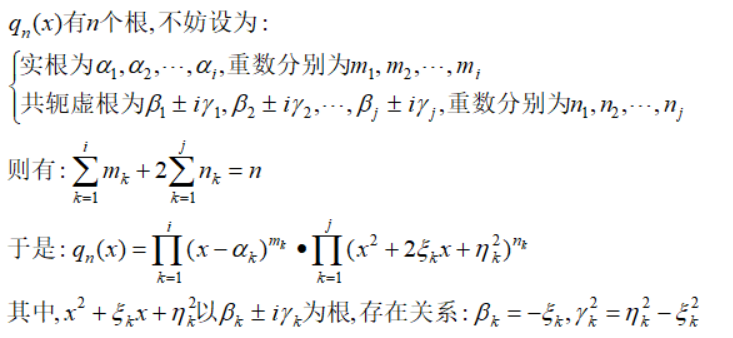
最后的关系可以根据根的乘积展开得到:
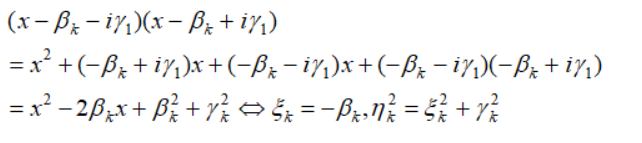
接下来我们希望对R(x)进行根式化简,首先对于实根,我们有:
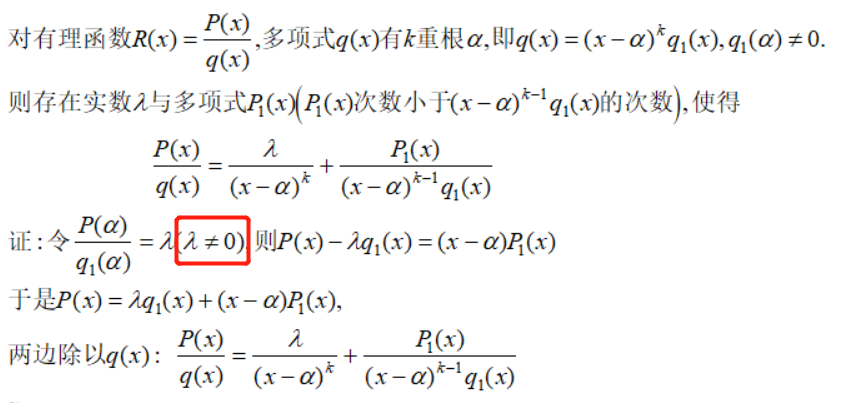
红色框需要说明一下为什么λ不等于0,因为若λ为0,则P(α)为0,则α为P(x)的一个实根,必然可以与分母q(x)约分,与题意假设矛盾。这样不断做下去,能把所有实根穷尽分解。接下来是虚根:
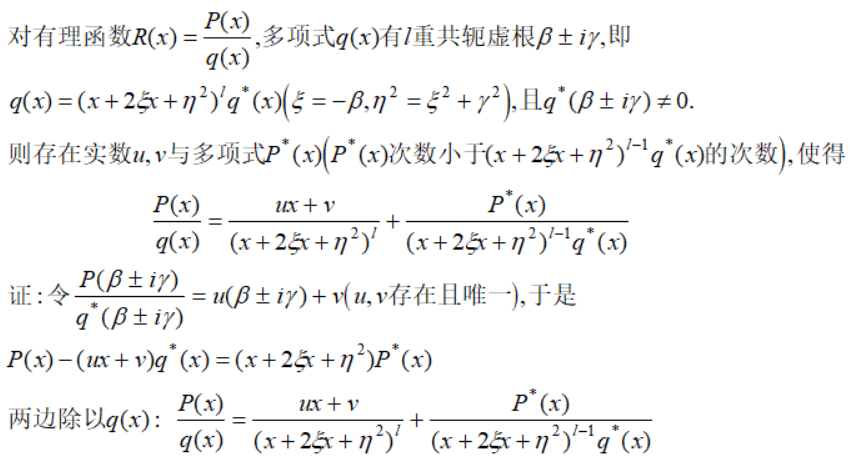
综上,我们可以把有理函数进行部分分式:
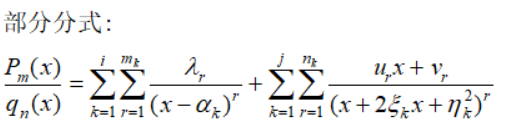
我们利用公式以及递推式,理论上必然可以求解上面的不定积分:
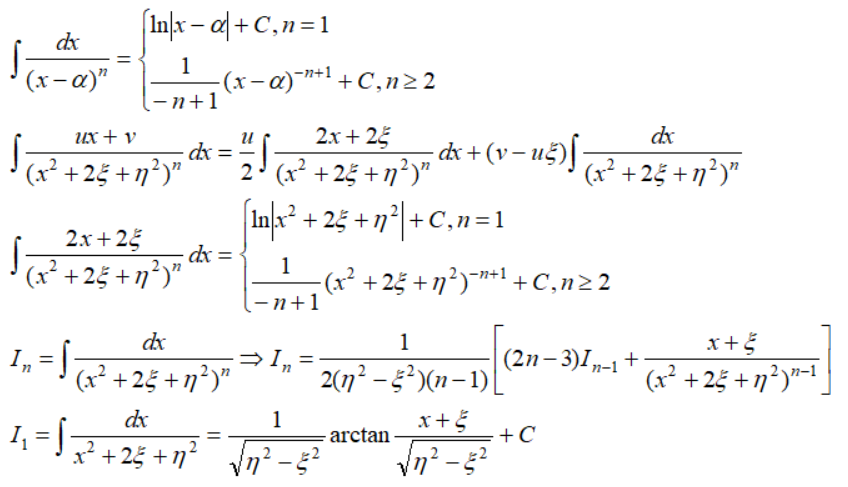
2
下面举个例子加以说明。
例1(待定系数法)
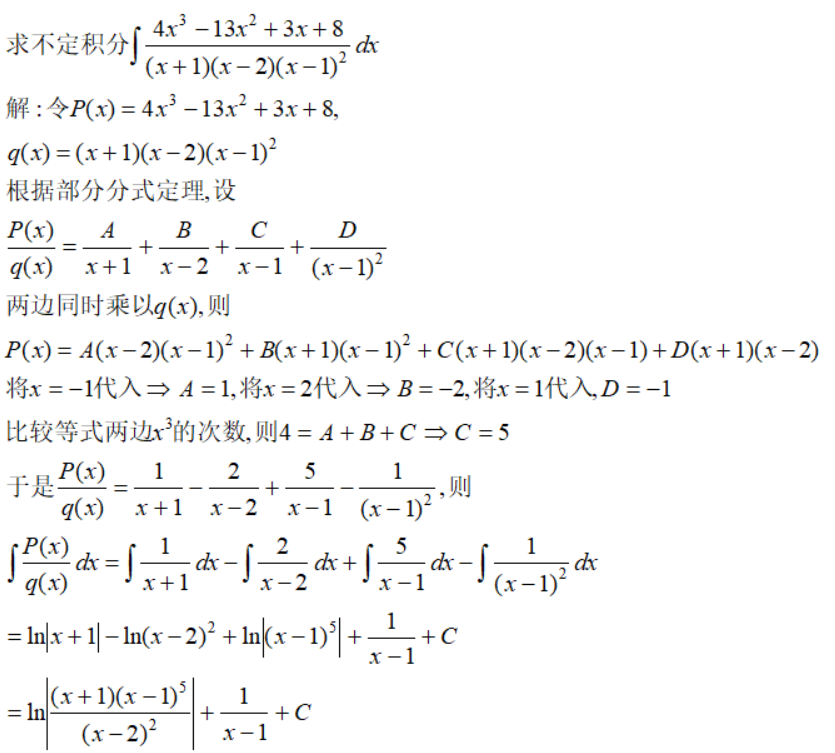
例2
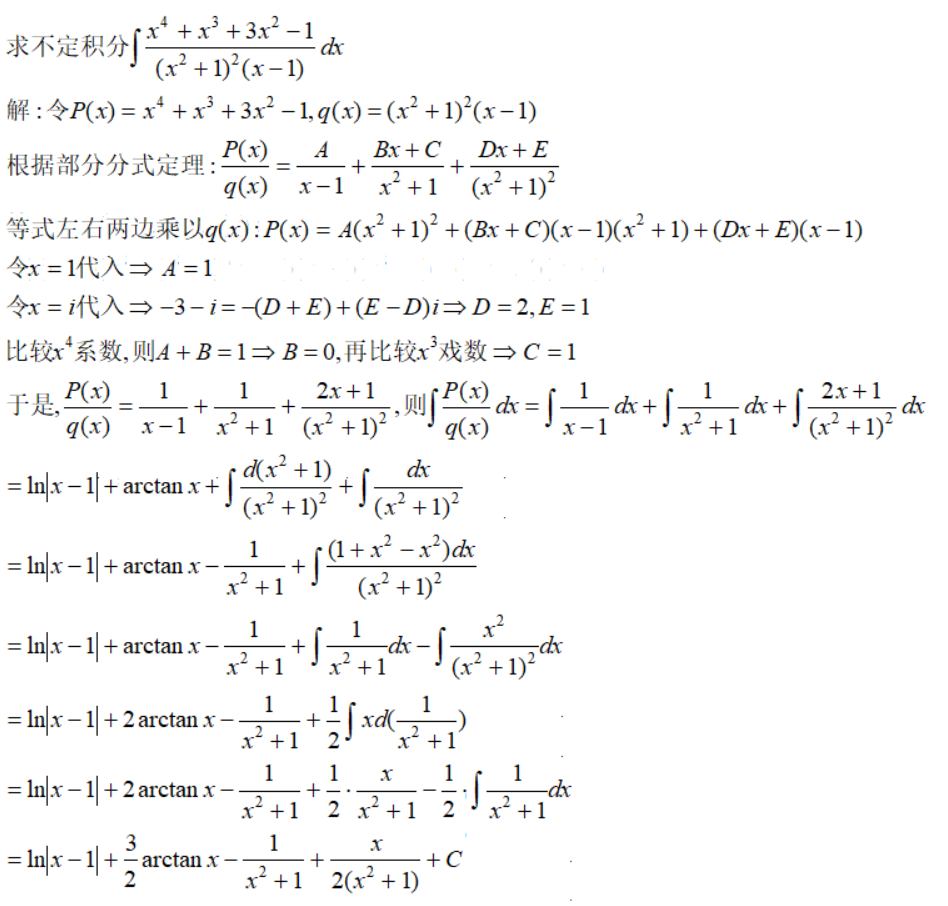
3
有一些无理函数可以通过变量代换为有理函数:

举个几个例子。
例3
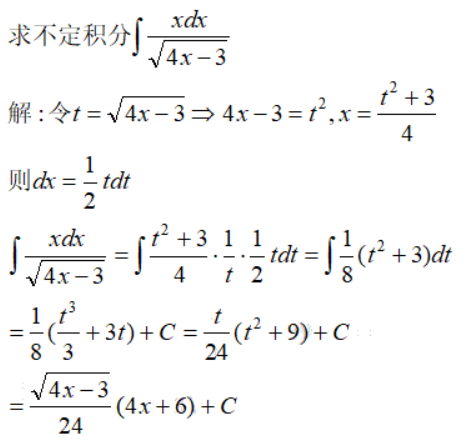
例4
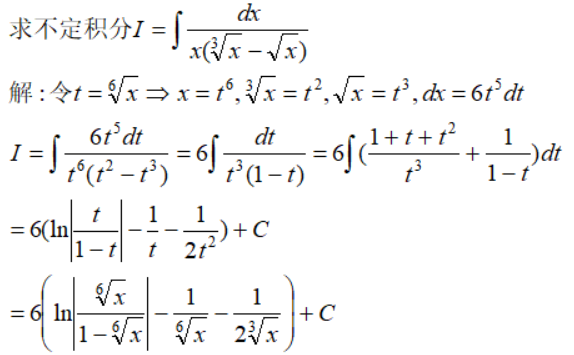
例5