向量b在多维子空间上的投影
回顾：任意向量b在另一个向量上（直线上）的投影
在研究向量在子空间上的投影前，先回顾一下前面学习的一个任意向量b在另一个向量a上的投影，共三个部分。
1，求权重系数
（A constant）
基于投影即分量的理论，一个向量b在另一个向量a上的投影p，是b在a方向上的分量。投影p与向量a的方向相同，但大小不同，而这个大小就是b在p（a）上分量的多少。因为，我们最先研究的是如何计算出向量a所乘的常数项权重系数。（这里我觉得叫英文中的scale也很贴切）
2, p (A vector)
有了前面的常数项系数/权重系数，我们就可以求出向量b在向量a上的投影p，其中a已知。
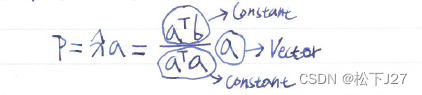
3, P (A matrix)
重新改变一下上式中的乘法顺序，就能找到可以把任何向量都投影到向量a上的投影矩阵P（下图中用红色方框框出的）。
从投影到列空间（向量在直线上的投影）：
把一个向量b投影到另一个向量a上，他不仅仅是投影到了一个向量上，他更是投影到了向量a所在的一条直线上，而这条直线就是向量a通过线性组合所张成的。如果把列向量a看作是一个nx1矩阵A中的列，那么a所张成的这条直线(一个一维子空间)就是矩阵A的列空间。这样一来，b在a上的投影就不单单是在一个向量上的投影，更是在A的列空间上的投影。
例：在二维空间
中，x轴和y轴分别是由列向量
，
所张成的两条直线。
如果把列向量看成是2x1的矩阵
中的列，把看成是2x1的矩阵
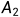中的列。则x轴和y轴这两条过0点的直线，就是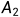，所张成的两个一维子空间(即，的列空间和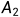的列空间)。在二维空间中的任意向量b，在x轴上的投影
和在y轴上的投影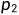
，实际上就是投影在了以为列的2x1矩阵的列空间上，和投影在了以为列的2x1矩阵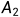的列空间上。
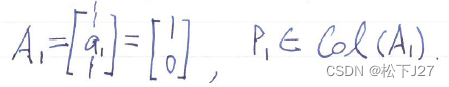
推广到多维：
设，列向量
(共m个元素)是多维空间
中的某个基向量。
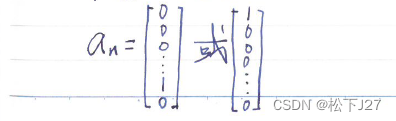
然后令列向量为mx1矩阵中的列，得到矩阵An。则，任意向量b，在所张成的直线上的投影
，实际上也是在nx1矩阵An的列空间上的投影，其中属于An的列空间。
从向量b在直线(向量)上的投影，到向量b在多维子空间上的投影：
前面说的b在直线（向量）上的投影，基本上可以看成是b在n维(当n=1时)子空间上的投影。当n>1时，我们投影的对象就不再是一条直线，而是一个平面，一个三维空间，或者是一个更高维度的子空间。
实际上，不论b在几维空间上的投影。只要牢牢抓住以下几个核心概念即可：
1，投影即分量
2，投影向量p在投影目标的子空间（列空间）内
3，什么是列空间
为了更好的理解如何计算向量b在多维子空间上的投影，我把研究过程分成了正向推导和逆向推导两部分：
正向推导：
我的正向推导过程，更多的是基于向量的几何关系和投影即分量的意义"直接"得到的。我们先从下面的这个例子开始。向量b=[1 2 3]'是
中的一个向量，它不在x-y平面上。而x-y平面，是由向量a1=[1 0]'和向量a2=[0 1]'所张成的一个二维子空间，它属于。现在，我们要把这个不在x-y平面上的向量b投影到x-y平面上。
根据投影即分量的原则，b在x-y平面上的投影p等于[1 2]'，这是根据几何关系直观得到的（向量b中的第三个元素，属于b在z轴上的分量）。这里，如果我们再进一步拆分，我们会发现，b在x-y二维子空间上的投影，又可以进一步被拆分成了p在另外两个向量a1和a2上的投影p1=[1 0]'和p2=[0 2]'。也就是说，b在二维子空间x-y平面上的投影p，等于它在x轴上的二次投影p1=[1 0]'和它在y轴上的二次投影p2=[0 2]'的和。
（注：[x x x x]' 表示列向量）
p1和p2是什么？那不就是向量b在向量a1所在直线x轴和向量a2所在直线y轴上的直接投影吗？！换句话说，通过对向量b进行多次投影/分解后得到的子投影p1和p2和把向量b直接投影到a1,a2上所得到的投影是一样的。
也就是说，要想找到b在x-y平面上的投影p，只需直接计算b在x轴(a1)和y轴(a2)上的投影p1,p2即可，因为他们二者之和正好等于我们要找的b在x-y平面上的投影p。
这样一来，我们就把求解向量b在二维子空间上的投影的问题，变成了直接求解向量b在x轴(向量a1所张成的),y轴(向量a2所张成的)上投影的问题，这是我们之前已经掌握了的知识。只需要分别求出a1前面的常数项系数
=1和a2所乘的常数项系数
=2即可。
如需求解b在更高维度子空间上的投影，只需要一一求出b在子空间每一个基向量上的投影，然后再把他们加起来就行了。即：
逆向推导：
前面的正向推导过程，我其实更多的是根据直觉(缺乏数学论证)，利用三维空间中的几何关系逐步分解b向量的过程（如果b所投影的目标子空间的维度非常大，就需要不断的对子投影分解，直到不能再分解为止。），它说明了b在子空间上的投影(分量)p等于多个子投影(子分量)p1,p2的和，且，计算p1,p2时，可以跳过一步步的分解过程，直接计算向量b在x轴和y轴上的投影即可。
逆向推导过程和前面不同，前面的三维空间是现成的（已知的），重在对于分解的理解。而逆向推导要用已知向量去构造子空间，更像是一个回溯/追根溯源的过程。最终，也会得到和前面相同的结论，更重要的是，在这一节，会推导出更加快速，更加通用的计算投影p的方法。（这也是教科书上常用的方法）
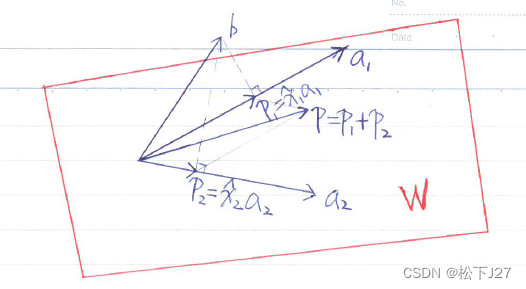
现有两个已知的线性无关向量a1,a2(共m个元素)，他们共同张成了一个二维子空间W。由于b在子空间W上的投影p必在W内，因而，p一定可以通过向量a1和a2的线性组合得到。即，以p=a1+a2的方式进行线性组合，其中，，都是常数，是向量a1,a2在进行线性组合时的权重系数。用线性代数的语言表示就是：
(注意，这里我只是暂时用和表示权重系数，还没有证明这里线性组合所使用的权重系数，正好等于b在a1,a2上的投影p1,p2的权重系数。也就是说，到目前为止，我还没有证明这里通过线性组合的方式"合成"投影向量p的两个分量a1,a2正好也是P在另外两个方向上的子投影p1和p2。所以，这里的和，只能看成是一个普通的常数项权重系数)
对上式进行改写，我们就能得到如下公式：
其中，矩阵A是向量a1,a2组成的矩阵，矩阵的第一列为列向量a1,矩阵的第二列为列向量a2。向量是由权重系数组成的列向量。
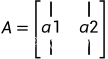
得到：
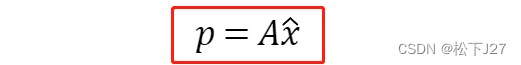
这个公式赋予了投影p另一层含义。即，子空间W不再只是a1,a2所张成的子空间，更是矩阵A的列空间。投影p不再只是a1和a2的线性组合，更是属于矩阵A的列空间。
A的列空间是什么？！A的列空间就是矩阵A中各列所有可能的线性组合。我所要找的投影p只是这众多组合中的一种，在本例中，这种组合各列所对应的权重就是和。
从2个线性无关的列向量到n个线性无关的列向量：
现在，我们把线性无关的向量个数从a1,a2,...一直增加到an个（假设每个列向量
都包含m个元素）。对于他们共同所张成的m维子空间而言，投影p一定可以通过a1,a2,...an的线性组合得到，对应的权重系数也从之前的两个变成了n个，，,...
。
改变乘法的顺序然后再展开有：
这样一来，向量b在m维子空间上的投影p就不单单是几个向量的线性组合，而是属于mxn矩阵A的列空间，其中矩阵A等于：
等于：
这样一来，我们要想求出向量b在m维度子空间上的投影，只需求出向量即可。(注意：和前面的说明一样，不论是我们这里的p1,p2...pn，还是，,...都不能看成是投影，也不能看成是一维投影中的投影系数，只能看作普通的数学符号。因为，我们暂时还没从数学上证明线性组合出投影p的所使用的权重，正好就是b在每个列向量上的投影所对应的权重系数，,...）
误差向量e正交于所要投影的子空间：
求解向量的秘诀，就在于巧妙的利用几何上的正交。
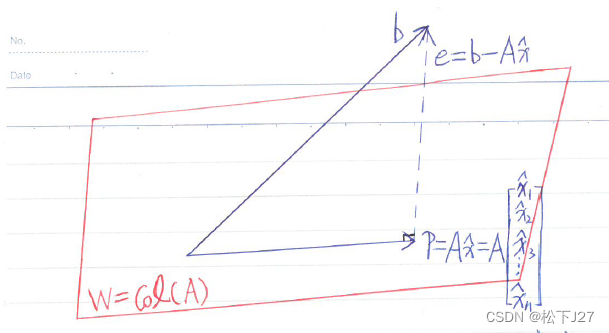
如图，n个线性无关的列向量a1,a2...an所构成的mxn矩阵A的列空间col(A)为W，属于。向量b在W上的投影为p，p在W内。p到b之间的误差向量e(mx1)为：
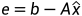
由于我们所求的投影p是b在某个多维子空间上的投影。故而，从几何关系上说：误差向量e不仅垂直于投影向量p, 更是垂直于整个子空间W，即,垂直于矩阵A的列空间W。又因为，A的列空间是由n个线性无关的列向量a1,a2...an所张成，且，这些向量也都在子空间内。
故此，误差向量e垂直于每一个列向量。根据两个相互垂直的列向量，他们的内积为0。有：
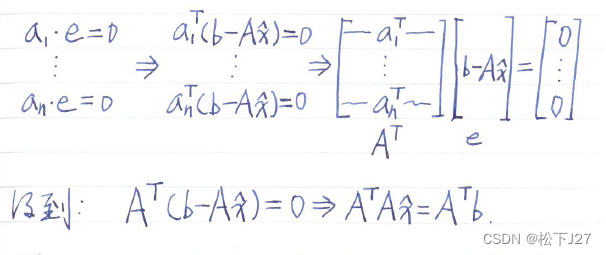
正好得到一个关于权重向量的方程(踏破铁鞋无觅处，得来全不费工夫!)，
是这个方程组的系数矩阵，A已知。
这样一来，我们就找到了可以一次性直接求出对应于a1,a2,....an的n个权重系数，,...的快速方法：
继而，我们就能直接求出向量b在m维子空间(A的列空间)上的投影p(mx1)，以及能把任意向量都投影到m维度子空间(A的列空间)上的投影矩阵P(mxm)：
我们把他和之前学习的一维投影，即，一个向量b在另一个向量a上的投影的结论做了一个比较：
这两个结果极为相似，一维投影中的1/
(一个常数的倒数)，在多维子空间的投影中变成了
(一个逆矩阵)。
1，对而言，一维投影是一个常数，而在多维中是包含n个权重系数一个向量。
2，对于投影向量p而言，一维投影表示的是一个对单个向量a的缩放(Scale)后的结果。而在多维矩阵中，表示的是多个对多个向量a的缩放后的综合结果。
A的左零空间的妙用：
上文提到，在求解向量时，基于误差向量e垂直于整个所要投影的子空间，因而也垂直于张成这个子空间的每一个列向量，这一几何关系求出了向量(nx1)：
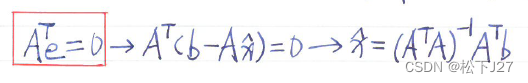
可如果我们再仔细看看上面我用红色方框框出来的方程，它其实还包含了另一层意思，那就是正因为误差向量e垂直于A的列空间，所以e属于A的左零空间。根据线性代数基本定理，A的列空间正交于A的左零空间，且，A的列空间与左零空间互为正交补，即：
也就是说，根据“垂直于A的列空间的任意向量，必然属于A的左零空间”这一定理，我们同样可以推导出计算向量的公式，得到和前面一样的结果。
总结：
（全文完）
作者 --- 松下J27
参考文献(鸣谢)：
1，线性代数及其应用，侯自新，南开大学出版社，1990.
2，Linear Algebra and Its Applications(Fourth Edition) - Gilbert Strang
3，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang
本文于2023年2月13日，修正了“A的左零空间的妙用”的一张插图中的错误。
本文于2023年3月对文中的一些不严谨的说法做了修改，对插图中的一些影响观看的水印做了处理，也修复了插图中的一些问题。
格言摘抄：
传统观念的死结就在一个“靠”字上，在家靠父母，出门靠朋友，靠上帝、靠菩萨、靠上天……总之靠什么都行，就是别靠自己，所以就只能在精神上跪着。 —— 丁元英《天道》
（配图与本文无关）
版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27