引言
想一下,在什么情况下可能需要将一个向量往一个子空间投影。在MIT的线代课程中,Gilbert教授给出了一种场景:即我们想要求解\(Ax=b\),但是\(b\)不在\(A\)的列空间中,此时我们希望在\(A\)的列空间中找一个离\(\overrightarrow{b}\)最近的向量\(\overrightarrow{f}\),求解\(A\hat{x}=f\),借由\(\hat{x}\)给出\(x\)的近似解。
矩阵乘法可以表示向量的线性变换,所以本篇笔记的主要内容是记录找到一个投影矩阵\(P\)的方法,通过左乘它完成向量对某一个子空间的投影,将向量\(\overrightarrow{b}\)转换为另一个向量\(\overrightarrow{f}\)。即:\(P\overrightarrow{b}=\overrightarrow{f}\)
平面上的投影
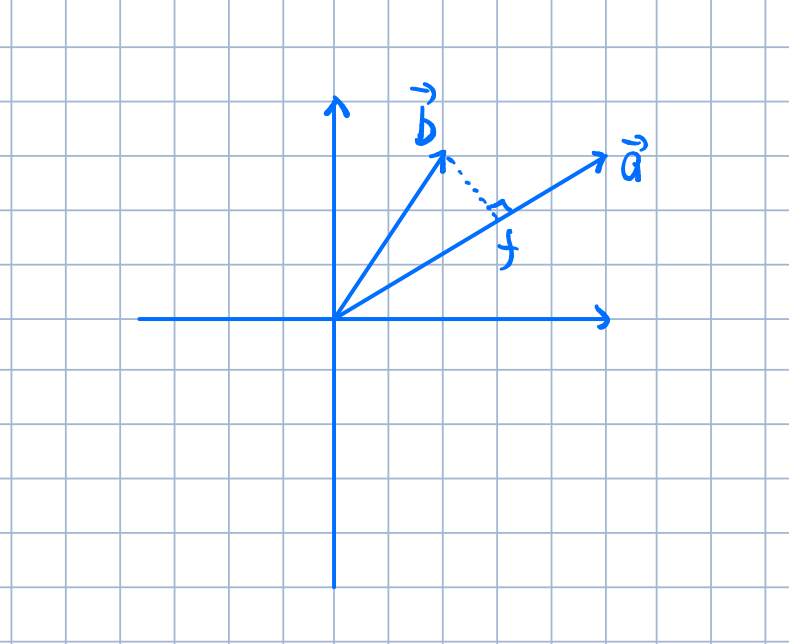
现在的情况如图所示,我们先来试着推导一下在平面中实现投影的投影矩阵长什么样子。我们想要将向量\(\overrightarrow{b}\)往\(\overrightarrow{a}\)上投影,现在已经在图上做出了投影的结果,即\(\overrightarrow{f}\)。那么,首先因为它俩是共线关系有:\[ \begin{equation} \overrightarrow{f}=λ\overrightarrow{a} \end{equation}\]
其次:\[ \begin{equation} (\overrightarrow{f}-\overrightarrow{b})\perp{\overrightarrow{a}} \end{equation}\]
知晓这两个关系,我们大概能推导出我们的结果了。将(2)的关系写成矩阵乘法的形式,应该有\[ \begin{equation} a^{\mathrm{T}}(λa-b)=0 \end{equation}\]
化简一下,去掉括号有\[ \begin{equation} λa^{\mathrm{T}}a=a^{\mathrm{T}}b \end{equation}\]
由于\(a^{\mathrm{T}}a\)是一个数,两边除以它可以推出\[ \begin{equation} λ = \frac{a^{\mathrm{T}}b}{a^{\mathrm{T}}a} \end{equation}\]
然后再把得到的λ代回到(1)中,我们已经可以写出一个投影矩阵了:\[ \begin{equation} f = aλ = a\frac{a^{\mathrm{T}}b}{a^{\mathrm{T}}a} = \frac{\ a\ a^{\mathrm{T}}}{a^{\mathrm{T}}a}b \end{equation}\]
我们已经得到了一个投影矩阵了,那就是\[ \begin{equation} P = \frac{\ a\ a^{\mathrm{T}}}{a^{\mathrm{T}}a} \end{equation}\]我们给这个矩阵一个符号\(P\)。不得不说我们上面推导过程中\(a\)和\(b\)放置的位置都是有选择的,要不然不会这么顺利推出投影矩阵。但是好在我们已经得出了结果。
平面上的投影矩阵P
所以现在来看下P的性质:
- 观察P我们会发现这是一个对称矩阵,即\(P^{\mathrm{T}}=P\)
- \(rank(P)=1\)
- \(P\)的列空间是什么,它的列空间是向量\(\overrightarrow{a}\)所在的一条过原点的直线。一个矩阵对应的列空间定义为矩阵内列向量的线性组合,很显然这些线性组合得到的向量都落在这条直线上。
- 而且还有一个很有意思的性质,即\(P^2=P\)。实际推导一下很快得出结果,而且从几何角度想,左乘两次P矩阵相当于往\(P\)的列空间投影两次,第一次投影在\(f\)的位置上了,而\(f\)本身就在\(P\)的列空间中,再往\(P\)的列空间投影显然还在\(f\)这个位置,就是它本身。
所以到这里为止,我知道了在\(R^2\)中,一个向量\(\overrightarrow{b}\)左乘上一个投影矩阵\(P\)相当于往投影矩阵\(P\)所在的列空间\(C(P)\)投影,能得到一个处于子空间\(C(P)\)中的向量\(\overrightarrow{f}\)。并且,只要我们知道\(C(P)\)的一组基,就能求出\(P\),比如在上面的例子中,这组基是单个向量\(\overrightarrow{a}\)。
三维空间上的投影
二维空间可能并说明不了什么问题,让我们试试三维,凭我们从小到大的数学直觉,一般认为三维比二维空间更有说服力,而且能将一些结论推向高维。下面还是画一个在三维空间的抽象图:

这个图可能不是很好看,反正就是表达有一个平面,一个向量\(\overrightarrow{b}\)对着它投影得到\(\overrightarrow{f}\)。这里的平面是\(R^3\)中的一个子空间,显然它由一组基张成。这组基由两个线性无关的3维向量\(\overrightarrow{a_1},\overrightarrow{a_2}\)组成,将它们写成矩阵的形式为\(A=[\overrightarrow{a_1} \ \overrightarrow{a_2}]\),它是一个3x2的矩阵。那么还是老样子,仿照二维空间得出投影矩阵的流程,我们先要从图中找出向量对应的关系。第一点,\(\overrightarrow{f}\)在\(C(A)\)中,因此\[ \begin{equation} f=A\hat{x} \end{equation}\]
写成\(\hat{x}\)是为了与引言对应起来。同时,既然\(\overrightarrow{f}\)为\(\overrightarrow{b}\)的投影向量,\[\begin{equation} (\overrightarrow{f}-\overrightarrow{b})\perp{C(A)} \end{equation}\]其中\(C(A)\)是矩阵A对应的列空间,在这里即那个平面。当然也可以表示成\[ \begin{equation} \left \{ \begin{array}{lr} a_1^{\mathrm{T}}(b-A\hat{x})=0 \\ a_2^{\mathrm{T}}(b-A\hat{x})=0 \\ \end{array} \right. \end{equation} \]将它重新写回矩阵的形式有\[ \begin{equation} \left[ \begin{matrix} a_1^{\mathrm{T}}\\ a_2^{\mathrm{T}} \end{matrix} \right](b-A\hat{x})=\left[ \begin{matrix} 0\\ 0 \end{matrix} \right] \end{equation} \]也就是\[ \begin{equation} A^{\mathrm{T}}(b-A\hat{x})=0 \end{equation} \]
酷,我们先不急着展开(12),研究一下这个等式。所以\(b-A\hat{x}\)在哪个向量子空间中?它应该在\(A^{\mathrm{T}}\)的零空间中,也就是在\(A\)的左零空间中。
等等,在这里平面是\(A\)对应的列空间,而\(b-A\hat{x}\)处于\(A\)对应的左零空间。我们知道\(b-A\hat{x}\perp{平面}\),所以矩阵对应的左零空间与列空间正交。而这个本身就是一个性质:矩阵对应的左零空间与列空间是正交的(这个在四个基本子空间的笔记中有证明)。所以我们无意间证明了这个性质。
现在我们可以展开(12)等到我们一直想要知道的投影矩阵了。通过移项我们最终能得到这么一个等式\[ \begin{equation} \hat{x}=(A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}}b \end{equation}\]
好吧,我其实省略了一步,为什么\(A^{\mathrm{T}}A\)一定可逆,它会不会不可逆?答案是\(A^{\mathrm{T}}A\)一定可逆。
\(A^{\mathrm{T}}A\)可逆的证明
我们前面已经知道\(rank(A)=2\),即\(A\)的列向量线性无关,所以\(Ax=0\)仅有0解。现在我们试着探究\(A^{\mathrm{T}}A\)的对应的零空间Nul(\(A^{\mathrm{T}}A\))。假设v是零空间中的一员。那么有\[(A^{\mathrm{T}}A)v=0\],那么左边式子左乘\(v^{\mathrm{T}}\)上式仍成立,即\[v^{\mathrm{T}}(A^{\mathrm{T}}A)v=0\]改变括号的位置,我们能得到\[(Av)^{\mathrm{T}}(Av)=0\]要使上式成立,仅在\(Av=0\)下才可能。而在一开始就说了,A的零空间仅有零向量,也就是说v=0时,\((A^{\mathrm{T}}A)v=0\)才会成立。所以\(A^{\mathrm{T}}A\)的零空间也仅有零向量,\(A^{\mathrm{T}}A\)对应的列向量线性无关,\(rank(A^{\mathrm{T}}A)=3\),行列满秩,矩阵可逆。
回到投影矩阵的求解
接着回到上面得到的(13)式,将它代回到(8)中,我们就能得到梦寐已久想知晓的投影矩阵了。我们将这个等式写出来:\[ \begin{equation} f=A(A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}}b \end{equation}\]
所以向量b的左边就是我们要求的投影矩阵P了,我们将劳动成果单独写出来\[ \begin{equation} P=A(A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}} \end{equation}\]
额,(15)式太复杂了,俺们将它化解一下吧。去掉括号,合并一下,得到了...单位矩阵\(I\)。不,肯定哪里出错了。是的,一开始给定的A是3x2的矩阵,A并不是方阵,所以并不能去掉括号得到\(A^{-1}\)。太好了,我们的成果保住了。
那么再来思考下,我们是在假设A是方阵的情况下,得到投影矩阵化简的最终形式是单位阵。嗯...仔细思考一下,这十分合理。我们一开始就是要将向量\(\overrightarrow{b}\)往A的列空间投影,那么现在A是个3x3的方阵,A张开的列空间就是三维空间\(R^3\)。一个\(R^3\)中的向量往\(R^3\)投影就是它本身,这个解释听起来很合理。
那么看来不能将(15)式化简了。我们再来将它和平面空间中得到的投影矩阵(7)对比一下。它们有相同的性质,比如都是对称矩阵,或者\(P^2=P\)。而且它们的形式也很相近。
好吧,我们最终得到了能将三维空间中将一个向量\(\overrightarrow{b}\)往一个子空间映射的投影矩阵\(P\)。矩阵乘法\(Pb\)的结果就是在这个子空间中有一个向量\(\overrightarrow{f}\),它是由\(\overrightarrow{b}\)投影得到。
总结
这个结论应该能被推向高维,即如果A不是3x2的矩阵,比如是4x3的矩阵。那么投影的过程就是四维空间中的一个向量\(\overrightarrow{b}\)往其中的一个三维子空间投影。这个子空间由3个线性无关的4维向量\(\overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3}\)张成,将它们写在一起能得到一个矩阵\(A=[e_1,e_2,e_3]\)。再借由(15)我们能得到投影矩阵\(P\),作矩阵乘法,我们就能得到一个向量\(\overrightarrow{f}\),它在子空间中,并且是向量\(\overrightarrow{b}\)往三维子空间投影的结果。