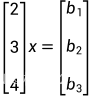向量在子空间上的投影与最小二乘逼近
对于一个mxn的非齐次线性方程组Ax=b而言，他可能有解，也可能没有解。如果A中各列通过线性组合可以得到b, 或者说b在A的列空间中，则方程组有解，即方程组相容。反之，则方程组不相容，无解或者说有无穷多解。
如果方程组的数量m大于方程组的未知数n，尤其是对于m(m>1)个一元方程组Ax=b而言，很有可能会出现方程组不相容/无解的情况。
3个一元一次方程所组成的方程组：
例如下面的这个方程组：
这个方程组要想有解，就必须要满足b在A的列空间中，即b可由A中的列向量[2，3，4]通过线性组合得到。也就是当且仅当b满足b1:b2:b3=2:3:4的比例关系，方程组x才有解，且是唯一解。
在我们的实际工作中，会有很多类似于上面这种方程组m的数量远大于n的情况。这些方程组Ax=b虽然无解，但又必须要解。一种办法是舍去方程组中的部分方程，用剩下的方程求x。比如说上面的这个方程组，如果我们基于这些数据的背景和原理，我们猜测第二个方程的b2，可能是个错误的数据。则，我们就可以舍去第二个方程，用第一和第三个方程去计算。
比如说，上述的三个方程中的未知数x表示的是一斤苹果的售价，b1,b2,b3分别表示购买了2斤，3斤和4斤苹果花了多少钱。假定我们得到了以下数据：
通过观察，我们猜测，第二个方程组3个苹果的总价似乎不那么合理。因为，苹果的单价为一个定值，随着我购买苹果的数量越来越多，那么苹果的总价应该越来越高。而第二个方程就明显不符合我们的预期。而且，如果我们稍微看一下第一和第三个方程，就能发现他们算出来的单价基本上都是在6元/斤左右，但第二行的算出来，似乎太便宜了。
因此，我们在求解这个方程组时，可以保留方程1,3，去掉方程2。最终得到一斤苹果的价格约等于(12.7/2+23.9/4)/2=6.125。
对于一些简单的问题和方程组的数量很少的情况下，我们可以试着用上面的方法去找到x的非精确解 
(读作，x hat)。但，这种"小儿科"的做法缺乏严格的数学理论支撑，也不科学。下面我会分别从微积分和线性代数这两个角度，来求解上述方程。
By Calculus:
对于更多的，更加普遍的，无解的mxn方程组，人们找到一种更好的，更加科学的解法，即最小二乘法。他在不舍弃任何一个方程(绝大多数情况下)的前提下，把分别代入m个方程中，能够尽可能的保证每个方程左右两边的误差都尽可能的小，即保证m个方程的整体误差最小。还是以本文开始处的方程为例，最小二乘算法的目的是要最小化方程左右两边误差的平方和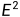
：
如若方程组Ax=b有解，则上述整体误差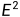=0，
。如果b与a不成比例，方程无解，就需要通过最小二乘的方法，找到一个非精确解，他使得的整体误差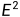最小。这样一来，我们的问题就变成了，如何求出令函数f(x)=min(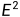)最小化的？
根据微积分的知识，我们知道，一个函数的极大值/极小值往往出现在斜率为0处，即，原函数的导数等于0的地方。（如果一个不断变化的函数图像停在某处不变了，往往都是函数图像中的波峰或者波谷处)
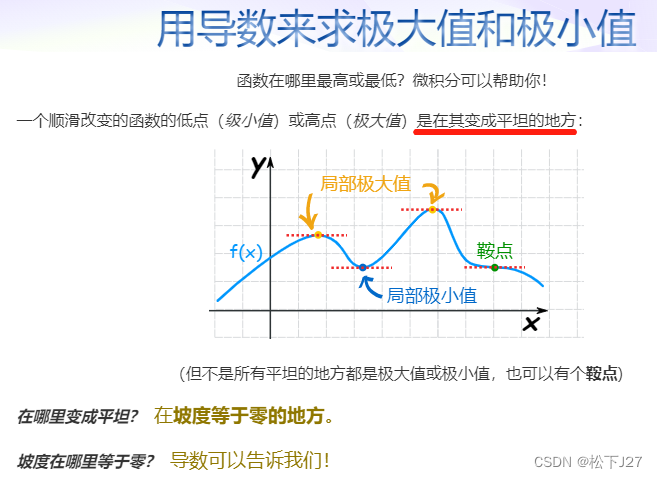
对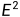求一阶导数，并且令他的一阶导数为0：
进一步化简后有:
然后，我们再基于该函数的二阶导数，来确定当前点的极值，究竟是极大值还是极小值。因为，函数二阶导表示的是原函数变化率的变化率（一个更好的理解方式是把函数的二阶导数理解成原函数变化的快慢。例如，物理上的加速度。）
若函数f(x)的函数值在某一点x=n处的一阶导f'(x=n)=0，即f(x=n+1)-f(x=n)=0，说明原函数的函数值在此处维持不变。若在f'(x=n)一阶导为0的基础上，f''(x=n)二阶导为负数。则，进一步说明函数在停止变化之前，是递增的。也就是说，函数值增加到一个峰值就不再增长了。那么，这个令一阶导为0的点x=n所对应的原函数的函数值f(x=n)，大概率是极大值点。
例如：一阶导突然从10变成了0，原函数从7增加了10变成了17后，就不再增长了，说明17可能是极大值。
原函数 |
0 |
1 |
3 |
7 |
17 |
17 |
17 |
17 |
10 |
9 |
5 |
0 |
|||||||||||
一阶导 |
1 |
2 |
4 |
10 |
0 |
0 |
0 |
-7 |
-1 |
-4 |
-5 |
||||||||||||
二阶导 |
1 |
2 |
6 |
-10 |
0 |
0 |
-7 |
6 |
3 |
1 |
反之，一阶导f'(x=n)为0，二阶导f''(x=n)为正数。说明函数在停止变化之前，是递减的。函数值减小到一定程度后，不再减少了。那么，这个令一阶导为0的点x=n所对应的原函数的函数值f(x=n)，大概率是极小值点。
例如：一阶导突然从-4变成了0，原函数从4降低到0后，就不再继续下降了，说明0可能是极小值。
原函数 |
20 |
15 |
5 |
4 |
0 |
0 |
0 |
1 |
8 |
9 |
10 |
15 |
|||||||||||
一阶导 |
-5 |
-10 |
-1 |
-4 |
0 |
0 |
1 |
7 |
1 |
1 |
5 |
||||||||||||
二阶导 |
-5 |
9 |
-3 |
4 |
0 |
1 |
6 |
-6 |
0 |
4 |
就本例而言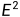，的二阶导数等于58，是一个正数。说明前面我们令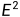的一阶导为0求出来的极值点，是一个极小值点，也正是我们需要的最小二乘解：
这个答案很有意思!马上我们就能看到，他把通过微积分求出来的，能够令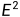最小的最小二乘解和线性代数联系到一起。
By Linear Algebra:
我们先把原方程组表示成矩阵ax=b的形式，其中列向量a=[2 3 4]',列向量b=[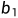
]'，得到：
若方程组有解，则向量b一定属于向量a所张成的列空间C(a)，即，b可以通过a的线性组合a*x得到。又因为，该方程组无解，所以a无法通过线性组合得到b，为了找到方程组的"替代解"，我们需要在a的列空间上找到一个最接近向量b的向量a*(实际上就是要找到)，使得这种线性组合a*与向量b的误差e=a*-b最小。事实上，我们要找的这个，位于a的列空间内的，距离b最近的向量a*，只能是向量b在a上的分量，即，b在a上的投影p。
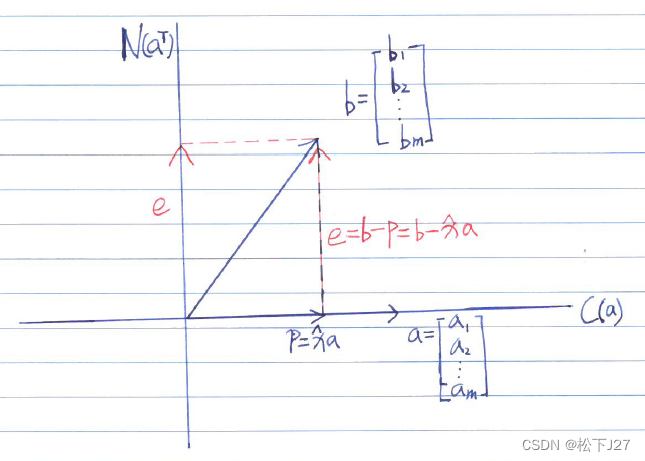
这样一来，我们就把原本无解的向量b，"拉/投影"到了a的列空间C(a)上，使得原本无解的方程组ax=b，变成了有解的方程组a=p。这一点，在下面的几何图示上看更加直观。
1，C(a), (column space of a)表示向量a的列空间，他是向量a所有可能的线性组合，是一条直线。因为，方程组无解，向量b不在向量a的列空间C(a)上。为了找到ax=b的解，就需在a上找到距离b最近的向量p=a，两个向量b与p的距离,就是向量e=b-p的长度【见附录1】。要想e的长度(点p与点b之间的连线)最小，p点，只能是点b到点直线a上的垂线与a的焦点。这个最接近b的向量只能是b在a上的投影p, 或者说是b在a的列空间C(a)上的分量。
2，向量b与投影向量p之间的距离等于，向量e=b-p的长度。当b与a之间的距离很近时(也就是两者的夹角很小），b很接近有解的列空间C(a)，误差向量e的长度很短。当方程组有解时，则b就是p，没有误差，e的长度为0。
3，N(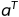
)，(Null space of 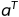)这是a的左零空间。因为，e垂直于a的列空间C(a)，所以，e属于a的左零空间，这两个空间两两正交且互为正交补。
基于上面的结论，e属于a的左零空间，有：
得到：
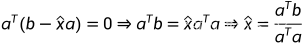
现在是时候回过头来看看，前面从微积分的角度得到的结果了：
注意看，等式右边的上半部分"2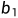+3+4"是什么，(如果用a=[2 3 4]'表示方程组的系数,用b=[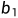 ]'表示方程组的右端) 这不就正是
吗？！
而等式右边的下半部分"
"，不也正是
吗？！
这样一来，前面通过微积分的知识求得的最小二乘解，就和后面用线性代数的方式得到的答案，完美的连到一起了！
对于同一个，在微积分中他是令原函数的一阶导为0的解。在线性代数中，他是非常熟悉，且十分重要的投影系数。(投影系数，指的就是向量a上的投影向量p的长度与向量a自身长度的一个比例)
也就是说，就本例而言，方程组的最小二乘解，就是线性代数中，求一个任意向量b在向量a上的投影向量p时，所需的投影系数。毕竟，投影向量p只不过是方向与a相同，大小与a成一定比例(这个比例就是投影系数)的一个向量。
m个一元一次方程所组成的的方程组：
现在，我们把上面的例子，推广到更普遍的情况。对任意单一未知数，m(m>1)个方程的一元一次方程组:
或
By Calculus:
基于微积分的知识，m个方程左右两边误差的平方和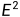为：
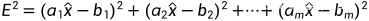
同样，为了最小化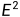，找到令他的一阶导为0的最小二乘解：
通过他的二阶导数,判断这个一阶导数为0的极值点是否为最小值，得到：
只要a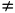
0，则他的二阶导数一定是一个正数，因此，令他的一阶导数为0的最小二乘解所对应的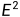，一定是一个最小值。
求解一阶导数的方程得到：
By Linear Algebra:
令系数向量a和等式右端向量b分别为：
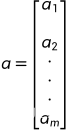和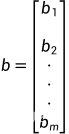 
上述m个一元一次方程组，就可以用矩阵的形式表示成ax=b。
因为，b不在a的列空间C(a)上，所以原方程组ax=b无解。为了找到最接近的/误差最小的解，我们把b投影到a的列空间上，得到有解的方程a=p。
为了求解这个方程，我们根据误差向量e垂直于a中的每一列，或是根据误差向量e属于a的左零空间。都能得到:
进一步得到：
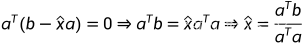
其中：
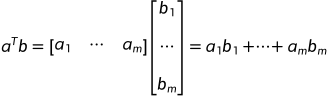
同样，线性代数和微积分得到了同样的结论：
补充：linear algebra + calculus
这里我再稍微提一下，在前面的论证中，我是分别从微积分和线性代数两个思路出发去解决一元一次方程组无解的问题，并得到的相同的结论和答案。实际上，我们还能通过线性代数+微积分的方式去思考，同样能够得到相同的结果。
结合几何图形来说，b不在a的列空间上，故而无解，此时，b与a的列空间之间的误差为e=b-p。把b拉到/投影到a的列空间上，方程才有解，这时，p与a的列空间的误差e=0。
也就是说，求解ax=b的过程，变成了最小化误差向量e的长度的过程【见附录2】，得到：
等式两边同时平方，得到：
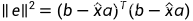
这样一来，利用线性代数中"向量的长度"的知识，得到：
为了最小化误差向量e的长度, 则需要用到微积分去求极小值，得到：
最终得到：
综上：对于a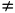0，且m>1的，一元一次方程组，他的最小二乘解为：
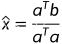
一些困惑和想法：
单从线性代数的教学方式和教科书的撰写方式来看，私以为求解最小二乘的最佳方式就是投影。简而言之就是，ax=b无解，是因为b不在a的列空间上。通过投影，得到有解的方程a
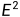=p。而，如果是微积分的方式，需要通过求的二阶导来判断令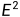的一阶导为0的极值点，究竟是不是我们想要极小值点？而利用线性代数中e与p垂直的概念(或e属于a的左零空间N(a)的概念)就不用求导来验证。
这也是为什么，gilbert strang的线性代数教科书要把最小二乘放在正交这一章讲，且放在整本教科书较为后面的位置。
最后：我给大家一个sweet and kind tips, 最小二乘解并不是原方程ax=b的解，他是新的方程a=p的解。
附录1：
附录2：
（全文完）
作者 --- 松下J27
参考文献(鸣谢)：
1，线性代数及其应用，侯自新，南开大学出版社，1990.
2，Linear Algebra and Its Applications(Fourth Edition) - Gilbert Strang
3，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang
格言摘抄：
《马说》
唐代·韩愈
世有伯乐，然后有千里马。千里马常有，而伯乐不常有。故虽有名马，祗（zhǐ）辱于奴隶人之手，骈（pián）死于槽（cáo）枥（lì）之间，不以千里称也。
马之千里者，一食（shí）或尽粟（sù）一石(dàn)。食（sì）马者，不知其能千里而食（sì）也。是马也，虽有千里之能，食（shí）不饱，力不足，才美不外见（xiàn），且欲与常马等不可得，安求其能千里也？
策之不以其道，食（sì）之不能尽其材，鸣之而不能通其意，执策而临之，曰：“天下无马！”呜呼！其真无马邪（yé）？其真不知马也！
（配图与本文无关）
版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27