多元方程组的最小二乘解与向量在多维子空间上的投影
在这篇文章中，我们把一元一次方程组ax=b的最小二乘问题，拓展到更为普遍的多元方程组Ax=b的最小二乘问题。之前的ax=b中的a是mx1矩阵，整个方程组只有一个未知数，a中只有一个列向量。现在我们要讨论的的方程组Ax=b有n个变量，矩阵A中有 n列。
此外，我们依然只关注方程组的个数m，大于未知数个数n的情形，也就是说观察点过多的情形。这样一来，方程组Ax=b大概率是不相容的/无解的，也就是说向量b大概率不在A的列空间C(A)内。
这里，我就不再从微积分的角度去计算最小二乘解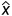
了，单单从线性代数的角度去分析方程组Ax=b。
假定Ax=b方程组为:
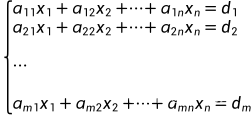
对应的矩阵A为：
其中 
依此类推
方程组无解，说明b不在A的列空间上，与一元一次方程组ax=b不同的是，原来的列空间C(a)是一条直线，而这里的列空间C(A)是一个平面或者更高维度的一个子空间。要想找到方程组的近似解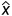，需要找到把b投影到A的列空间上，得到投影p。且，误差向量e=b-p。
下图为3x2矩阵的示意图，供大家参考。该方程组共有两个列向量column 1和column 2，他们共同张成了A的列空间column space, 一个平面。对于更大维度的列空间无法用几何图像来表示，但可以结合下图理解。
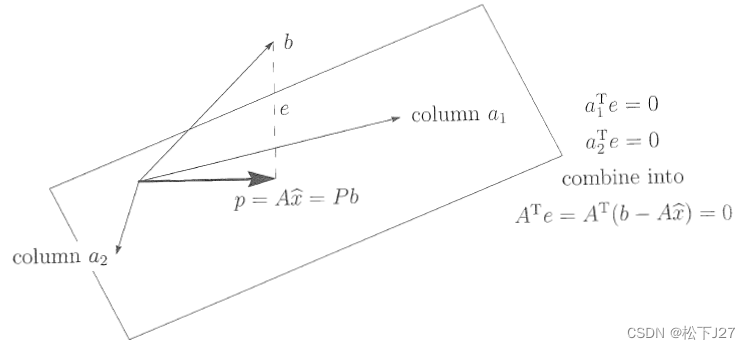
最后，要么基于误差向量e垂直于A中的每一个列向量col(
)，要么是利用任何垂直于A的列空间的向量都属于A的左零空间，得到误差向量e属于A的左零空间N(A)，两种方式都能求得最优解。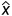
1，根据任何垂直于A的列空间C(A)的向量都属于A的左零空间N(
)，且，误差向量e也垂直于C(A)。因此，误差向量e属于A的左零空间N(A)，得到：
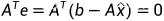
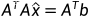
2，如果是基于因为误差向量e垂直于A的列空间C(A)，故而垂直于A中的每一个列向量column a1, column a2 .... column an，得到：
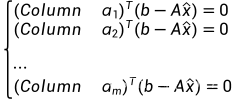
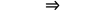
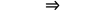
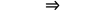
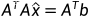
最终得到了和前面一样的结果。
Attention!
上述两种方法所得到的结果正是最小二乘的核心方程！
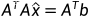综上：原方程组Ax=b无解，一个“unofficial”的方法是方程左右两边同时左乘得到一个新方程，求解这个新方程(这就是人们常说的“正规方程”)，得到最优解/最小二乘解。
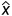不论A是什么矩阵，
都是方阵，且是一个对称矩阵，可逆的前提条件是矩阵A中的各列是线性无关的。如果可逆，则正规方程的最优解为：
b在列空间上的投影为：
现在我们找一个3个方程2个变量的方程组，实际练习一下求解方程组的最小二乘解。这个例子既便于我们利用投影即分量的概念，非常直观的找到答案，同时，也需要我们结合上面推到出来的计算方法加以验证。
A的列向量是由三个元素组成的，因此，A中各列的线性组合可以张成一个
的三维列空间。又因为A中的两个列向量的最后一个元素都是0, 且前两个元素线性无关，因此，他只能在三维空间中张成一个二维的x-y平面。根据投影即分量的直观理解，向量b=[4 5 6]' 在x-y平面上的投影只能是p=[4 5 0]，也就是说b在x上的投影为4，b在y上的投影为5，z轴不存在，因此b在轴上的投影为0。这都是通过投影的概念的直观感受得到的，下面我们需要通过详细的计算来验证这个结果：
方程左右两边同时乘以：
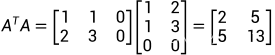
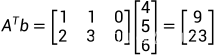
对A求逆：
计算最小二乘解：
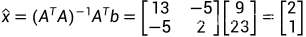
最终得到：
这一结果和我们通过观察直接得到的结果一样。
事实上，如果细心观察，不满发现，我们最小二乘的核心方程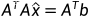，实际上就是我们之前说到的“通过投影，使得原本无解的方程组Ax=b，变成了有解的方程组A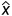=p”中的新方程A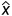=p。
其中，投影矩阵P为：
带入投影矩阵后：
两边同时左乘，得到：
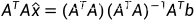
最终得到最小二乘的核心方程：
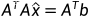
（全文完）
作者 --- 松下J27
参考文献(鸣谢)：
1，线性代数及其应用，侯自新，南开大学出版社，1990.
2，Linear Algebra and Its Applications(Fourth Edition) - Gilbert Strang
3，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang
格言摘抄：
“我希望在自己的墓志铭上只刻5个字：褚时健，属牛。”--- 褚时健
（配图与本文无关）
版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27