投影矩阵P
在前面的两篇关于投影的文章中,我们的学习重点分别是:
1,如何计算一个任意向量b在另一个向量a上的投影。也就是计算投影系数和投影向量p(小写)。
2,进一步加深投影即分量的理解。看到了任意向量b,在x,y坐标轴上的投影p1,p2,恰好且正好等于向量b在这些相互正交向量x,y上的分量。
而学习投影矩阵的主要目的是:看看怎么把任意向量b投影到a上。换句话说,在前面的学习中,我们找出了向量b在二维平面中,分别在x轴和y轴上的两个相互垂直的投影/分量:
(Find x hat)
(Find x hat)
也计算出了向量b在三维平面中,分别在x-y平面和z轴上的两个相互垂直的投影/分量:
(Find x hat)
(Find x hat)
但“怎么”把空间中的一个任意向量b投影到这些我们指定的坐标轴上?就要用到我们这里要学习的投影矩阵P(用大写的英文字母P表示),即:
比如说,我们要把任意向量b投影到向量a上,我们只要算出了投影系数就等于知道了投影向量p,但怎么把b投影到a上呢?就需要用到投影矩阵P,让这个矩阵P左乘向量b,就能得到同样的投影向量p,即如下关系:

更进一步说,前面学习的投影向量或投影系数,更像是在研究从向量b ---> 向量p(在向量a上),这种一对一的关系。而投影矩阵更像是在研究多对多的关系,有了投影矩阵P(对应于向量a的)以后,就可以把空间中所有的向量b,c,d,e,f.....等,通通都投影到a上,得到投影向量p_b,p_c,p_d.....等。
比如说,我们有了可以把任意向量都投影到x轴的投影矩阵P以后(注意:这里投影矩阵P是 专门针对于x轴的矩阵),那么只要把投影矩阵P右乘空间中的任何一个向量v,就能把这个向量投影到x轴上了,并且得到投影向量p=Pv。
小结:研究投影向量/投影系数更像是在研究How much? 而研究投影矩阵更像是在研究How?
如果计算投影矩阵

p的左边是一个矩阵乘以一个向量(所要强调的是投影矩阵P),p的右边是一个常数乘以一个向量(这里要强调的是投影系数的计算)。
二维空间中的投影矩阵
通过前面的投影即分量的学习,我们已经求出了,在二维x-y平面中,任意向量 b在x轴和y轴上的投影向量p1=[x 0]'和p2=[0 y]'。现在我们看看究竟是什么样的投影矩阵P? 才能把b投影到指定的方向上,即x轴方向和y轴方向。严格意义上说,不只是把b,而是可以把所有的矩阵都投影到指定的方向上。(请大家特别注意:我在文中专门用小写的英文字母p表示投影向量,用大写的英文字母P表示投影矩阵)
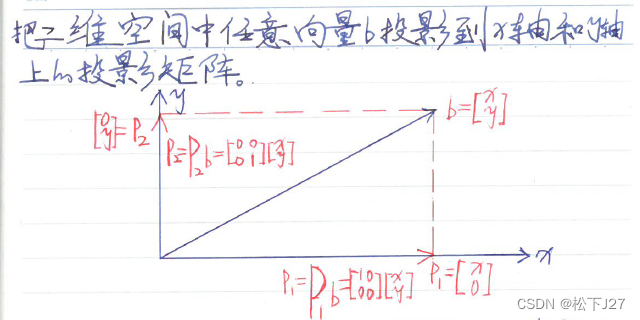
根据投影矩阵P的计算公式(a表示P所对应的投影的方向):
分别算出:
1,可以把任意向量都投影到x轴方向上的投影矩阵P1。
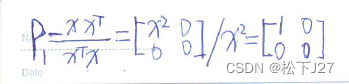

2,可以把任意向量都投影到y轴方向上的投影矩阵P2。
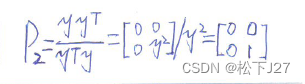

用投影系数/投影向量的方法算出来的投影p和用投影矩阵的方法算出来的投影p相等,且,不仅向量b的两个投影向量/两个分量p1,p2,他们两两正交且互为正交补。同时,p1,p2所对应的两个投影矩阵P1,P2的和正好等于相同维度的单位矩阵I。

且有:
也就是说,无论时把向量b投影到某个方向上多少次,得到的,依然还是同一个投影向量p,即:
投影矩阵P不可逆。
三维空间中的投影矩阵
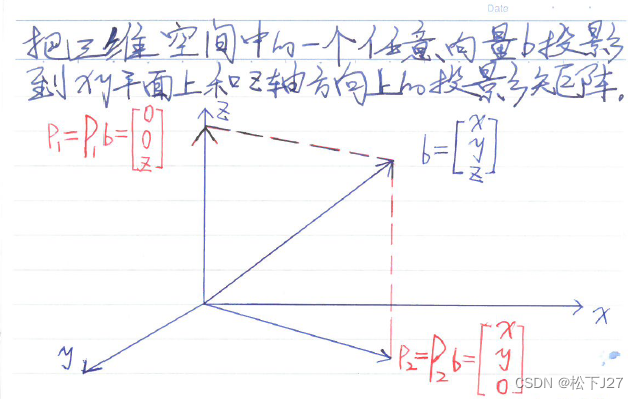
1,可以把任意向量都投影到z轴上的投影矩阵P1为:
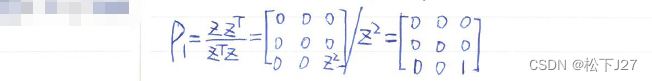

2,可以把任意向量都投影到x-y平面上的投影矩阵P2为:
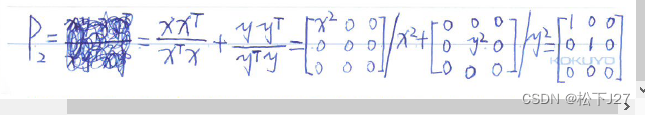


不论是通过投影系数计算还是用投影矩阵计算,两种方式都能得到相同的结果:
例:find向量b在向量a上的投影
这是之前用投影系数计算出来的结果:

这是用投影矩阵计算的结果:p=Pb

用投影矩阵证明,两个互相垂直的向量在彼此方向上的投影为0向量:

(全文完)
作者 --- 松下J27
鸣谢(参考文献):
1,《Introduction to Linear Algebra》,5th Edition - Gilbert Strang
2,线性代数及其应用,侯自新,南开大学出版社,1990.
金句赏析:
我听爷爷讲了一个故事
故事里的事是那昨天的事
故事里有好人也有坏人
故事里有好事也有坏事
故事里有多少是是非非
故事里有多少非非是是
故事里的事说是就是 不是也是
故事里的事说不是就不是 是也不是
故事里的事说是就是 不是也是
故事里的事说不是就不是 是也不是
故事里的事也许是已真实
故事里的事也许是从来没有的事
其实故事本来就是已故事
故事 就是故事 故事就是故事

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27