
笔者在投影这一系列的开篇就说过,我在学习投影的过程中,有很长的一段时间都是把重点放在了,如何计算投影本身,也就是背公式上。
现在我发现(尤其是明白了投影即分量之后),学习投影的主要目的(或者说是学习重点),并不是如何计算任意向量b在空间中另一个方向a上的投影,向量p。而是要思考为什么我们要绞尽脑汁把一个向量b,投影到我们希望的目标向量a或目标子空间S上(例如,三维空间中的x-y平面)?
因为,我们所要投影的目标向量a或者目标子空间S,都是可以通过他们所在的子空间的基底Base线性组合得到。或者说,我们所要投影的目标不单单是某个向量a或者说某个子空间S,而是某个nx1矩阵的列空间或者是某个nxm矩阵的列空间。

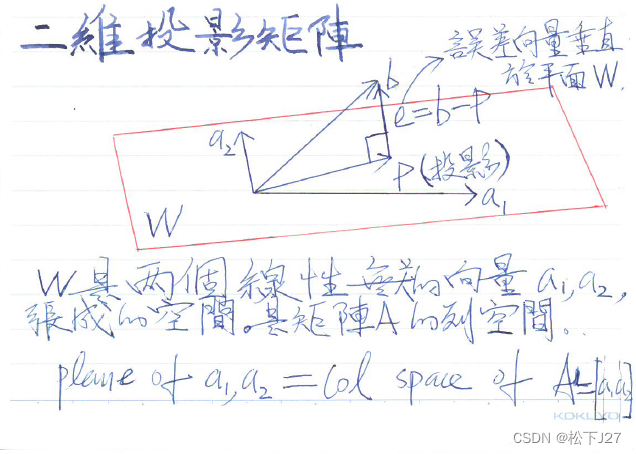
现在我们再回到这幅图(将就看):

这是一个二维空间,x轴与y轴分别是这个空间的两个子空间,他们过0点,且线性无关。
对于子空间x轴而言,他是一个一维子空间,属于:
我们定义列向量b1=[1 0]'为他的基底(Base)。(注意,基底不唯一,也可以是向量[n 0]'。)
子空间中的任何一个向量都可以由他的基底张成(Span)。例如,x轴上的向量[5 0]',可以由5乘以基底b1的线性组合得到,即,5xb1=5x[1 0]'=[5 0]'。且,基底通过线性组合可以张满整个子空间。现在我们从矩阵的视角来看看,如果我们把基底b1=[1 0]'当作2x1矩阵A的列向量,即:
这样一来,向量b在x轴上的投影p1(也就是在子空间x轴上的投影),就变成了b在A的列空间上的投影。而它,可以通过A中各个列向量的线性组合得到。
对于子空间y轴而言,他也是一个一维子空间:
我们定义列向量b2=[0 1]'为他的基底(Base)。
把基底b2=[0 1]'作为A的列向量,则:
对于三维空间而言(凑合看):

对于z轴而言,他是中的一个一维子空间,属于
:
令,列向量b3=[0 0 1]'为该子空间的基底(Base),让基底b3=[0 0 1]'作为3x1矩阵A1的列向量。

这样一来,投影向量p1=[0 0 z]不仅仅是向量b=[x y z]在子空间z轴上的投影,更是b在矩阵A1的列空间上的投影。如此一来,b就可以通过A1中各个列向量的线性组合得到,且,A1的列空间(即,A1中列向量所有可能的线性组合)就是z轴,因为A1各列的线性组合可以张满整个z轴。
对于x-y平面而言,他是中的另一个二维子空间,属于
:
令,列向量b1=[1 0 0]',b2=[0 1 0]'为该子空间的基底(Base),让基底b1=[1 0 0]'和b2=[0 1 0]'作为3x2矩阵A2的列向量。

则,投影向量p2=[x y 0]'既是向量b=[x y z]在子空间x-y平面上的投影,更是b在矩阵A2的列空间上的投影。如此一来,b就可以通过A2中各个列向量的线性组合得到,且,A2的列空间(即,A2中列向量所有可能的线性组合)就是x-y平面,因为A2各列的线性组合可以张满整个x-y平面。
从投影到最小二乘:
继续前面的二维空间的例子:

1,向量b=[x y] ——投影在x方向——》得到投影向量p1=[x 0]'
2,投影向量p1,在矩阵A的列空间中,且,A的列是由基底b1=[1 0]'组成的。
3,这样一来,向量b在x轴或y轴上的投影/分量p1,就可以通过矩阵A各列的线性组合表示了。
4,现在可以把前面反复提及的向量b和线性代数中最常见的方程组Ax=b放在一起考虑。把向量b放在方程组的右端,如果方程组有解,则说明,向量b在A的列空间中,也就是说b在A的列空间上的投影就是它自己。因为,有解就说明向量b可以通过A的列向量的线性组合表示。
现在令b=p1=[x 0],那么b就可以通过x轴的基底b1表示,b=x*b1[1 0]。
对于用基底作为A中各列的方程组Ax=b(p1)而言:
(A的第一列等于b1)
,方程有解
5,可实际情况是方程组Ax=b的b并不等于p1[x 0],而是b=[x y]。很明显方程组无解,因为,仅仅只是用[1 0],是无论如何都得不到[x y]。这时,为了让方程有解,我们只能把b投影到A的列空间上,也就是x轴上,找到一个最接近原方程Ax=b的近似解x',把求解原方程组Ax=b变成了求解新的方程组Ax'=p1,最终得到x'=x。
小结:

把任意向量b投影到某个子空间上,也就是投影到与之对应的mxn矩阵的列空间上,这样一来,原本无解的方程Ax=b,就变成了可求解的Ax'=p。(这是最小二乘的核心)
课外阅读(个人笔记补充):


(全文完)
作者 --- 松下J27
鸣谢(参考文献):
1,《Introduction to Linear Algebra》,5th Edition - Gilbert Strang
2,线性代数及其应用,侯自新,南开大学出版社,1990.
外国哲理小诗分享:
黄色的树林里分出两条路,
可惜我不能同时去涉足,
我在那路口久久伫立,
我向着一条路极目望去,
直到它消失在丛林深处。
但我却选了另外一条路,
它荒草萋萋,十分幽寂,
显得更诱人、更美丽,
虽然在这条小路上,
很少留下旅人的足迹,
那天清晨落叶满地,
两条路都未经脚印污染。
啊,留下一条路等改日再见!
但我知道路径延绵无尽头,
恐怕我难以再回返。
也许多少年后在某个地方,
我将轻声叹息把往事回顾,
一片树林里分出两条路,
而我选了人迹更少的一条,
从此决定了一生的道路。

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27