注意:这里是JAVA自学与了解的同步笔记与记录,如有问题欢迎指正说明
目录
前言
本篇是基础数据结构的最后一篇。因为个人之前确实没写过二路归并的迭代代码,因此此代码是在根据老师的代码生啃得到的代码理解,部分不完善欢迎指针。希望以这个代码为我们的基础数据结构篇专门算法讲解画上句号。
一、关于归并排序及其基础思想
归并排序是一种非常高效的基于递归实现的高级排序,也是所有高级排序中唯一一个稳定的高级排序算法,这个排序思想最早由我们“ 现代计算机之父 ”冯 · 洛伊曼最早提出的。归并排序利用三大算法之一的分治法,同时结合了有序数组合并的思想。
所谓的分治法,是由3步核心构成:分解(Divide):将原问题换分为n个规模较小而结构与原问题相似的子问题,也就是各个问题是独立的、解决(Conquer):递归地解决这些子问题、合并(Combine):然后再合并这些结果,得到原问题的解。其实分治法我们并不陌生,快排的枢轴分割思路其实也是一种分治,只不过其分割的判定过程要比归并复杂,因为其需要实现确定枢轴的位置。
关于有序数组合并其实是顺序表的一个经典案例。在这个案例中将给你两个有序线性表\(L\)与有序线性表\(S\),让你将两个表合并为新表,同时在新的线性表中,元素之间的有序性依旧可以保障。当然,做个操作格外简单,只要设置三个指针,分别指向线性表\(L\)、线性表\(S\)以及创建的空表\(M\),在每个表中逐步推进指针,推进条件是指向\(L\)与\(S\)的两个指针中最大元素赋给表\(M\)指针所指的位置,然后赋值方与被赋值方的指针前进。

这个过程不仅简单,而且非常快、且能适用于线性表与顺序表,只需要\(O(N)\)的复杂度即可完成有序表的组合。而我们的归并正式采用的如此的思维路径,因此这个操作将有序的集合扩大了而并没有限制\(L\)与\(S\)的长度,我们可以认为总线性表是由\(L\)与\(S\)分别连接构成的有序集,那么其中的\(L\)是否也可以理解为由\(L_{2}^{'}\)与\(L_{2}^{'}\)构成?\(S\)亦如是。于是试着将解决问题规模的缩小过程用一个二叉树来表示:
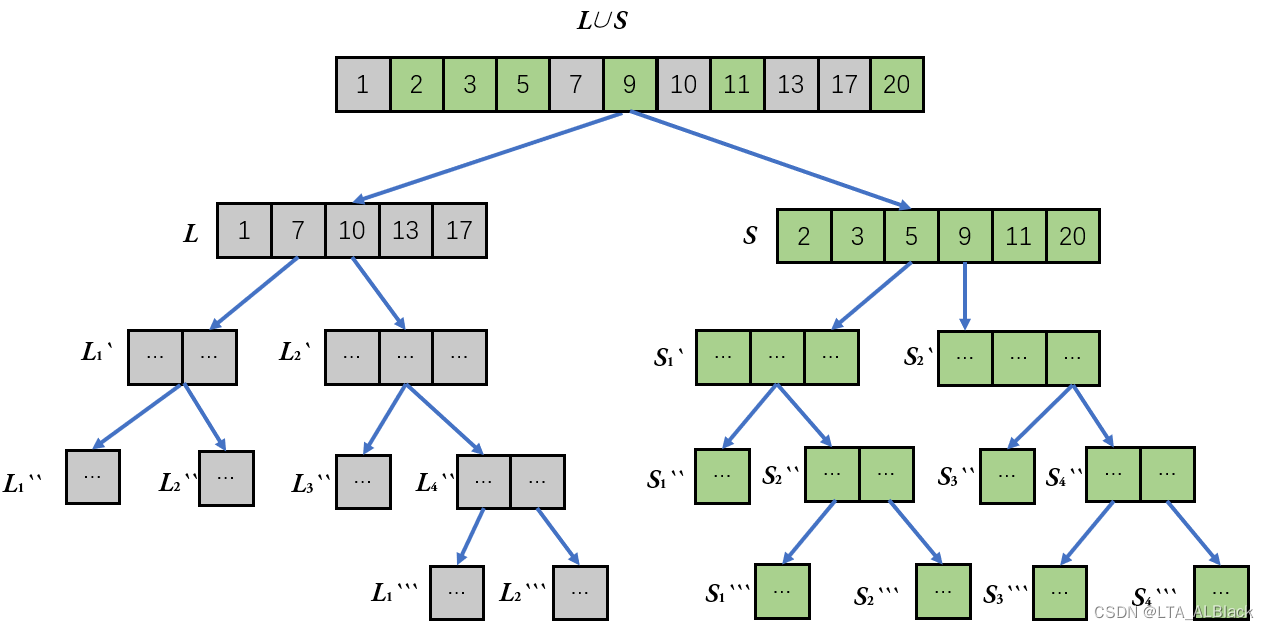
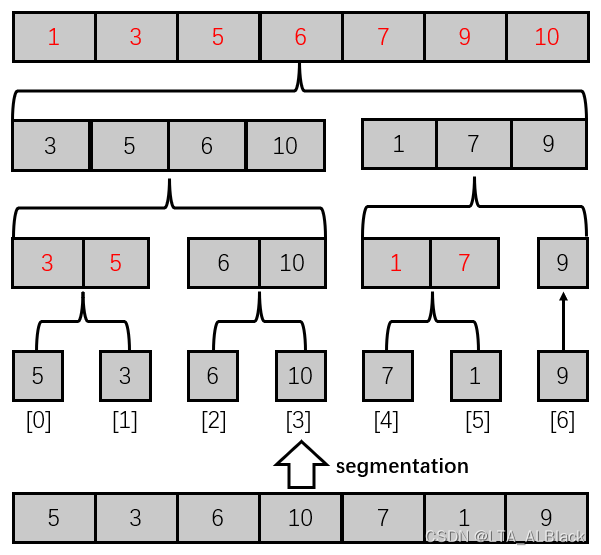
可以发现,最终我们的问题缩小为将两个单个的元素合并为一个有序序列,缩小到这个步骤已经能够确定地完成一次合并操作,毕竟就单个元素本身已经没有有序这种说法了。而这个步骤可以认为是递归的返回特征,因此我们可以自底向上地,通过顶部的不断递归直到底层,然后通过回溯操作实现自底向上的有序序列合并,最终回溯完最后的序列即是全体有序的一个序列。这就是二路归并排序的递归实现,一个基于递归与有序序列合并操作的高级排序。
当然,有序数组的合并问题并不局限于两个数组的合并,多数组之间也可以合并,若依据多数组合并,构成的递归树便是\(N\)叉树,以此设计的便是\(N\)路归并排序,今天我们只讲述常见的二路归并即可。
二、归并排序的迭代实现
1.迭代为什么要比递归复杂
初学归并排序的小伙伴建议先去学习一下归并的递归代码再来了解下本篇的迭代思路,因为为了讲解方便,我将默认读者已经在明白基本递归实现的归并排序的基础上说明代码(因为这个代码我也是在老师代码的基础上通过个人理解完成的)
首先要明白,归并本质上是对于数组的每个点切分,然后每个切开的相对孤立的顶点之间的俩俩合并(若是二路归并的话)如果按照递归的思路,那么我们会先从中间切一大刀,然后对于每个分块再度一刀切,不断细化...最后得到最小的块后,再回溯进行重拼。但是迭代思路的话,我们是在最开始就知道我们只需要将这个蛋糕切成什么样,我们从线性表的开头,一点一点,一段一段像切葱一样分开。切完之后,每隔开一定距离,我将这部分再合并为新的一段;当前合并完了之后,我重新扩大距离,进一步合并新的一段;如此反复....
综上所述,我可以总结这样的结论:
递归是先从最大块开始分段,逐步分到底层最小单位,然后回溯拼接,是一个先从上往下走,走到底再逐步向上,这样一下一上的过程。向上回溯合并时因为最初从上外下走时是二分式地走,于是回去的时候原路返回就好了——翻译过来就是递归已经帮我们解决块范围的问题了。而迭代法是直接从下往上走,它没有递归那种自上而下的途中奠定的路径辅助,这也是为什么迭代法在确定切片范围时设置非常麻烦的指针辅助!
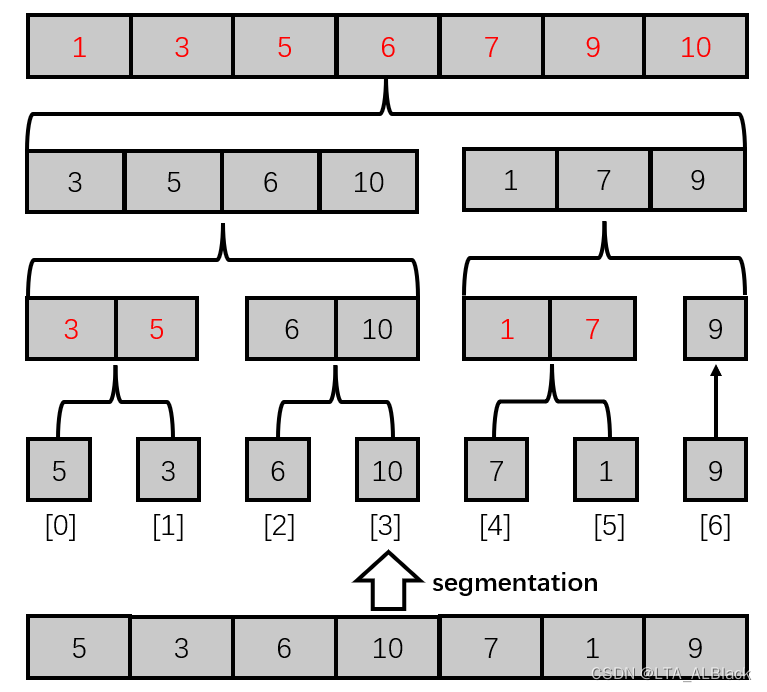
2.代码解释
上图就是归并的第一个基础过程,我们最初的数据是底部分散未合并的数据。代码大体的思路是我们备份两个并排的数组:
DataNode[][] tempMatrix = new DataNode[2][length];
// Step 2. Copy data.
for (int i = 0; i < length; i++) {
tempMatrix[0][i] = data[i];
} // Of for i这个数组的作用是用于模拟每次递归时需要的空间,因为每次递归都需要给出一个空余出一个可以操作的空间用来存放当前递归空间下进行有序数组合并的空间。由于每次分配空间过于麻烦,于是我们设置两个数组空间用来相互转换。比如从第一层数组俩俩归并到第二层数组,可以从DataNode[0][ ]转移到DataNode[1][ ],这时DataNode[0][ ]就没用了,于是其再次作为一个可用的空间,在从第二层归并到第三层时将DataNode[1][ ]的数据转移到DataNode[0][ ]。后续依旧如此反复,就如同我有两个杯子,来回捣腾同一杯水。
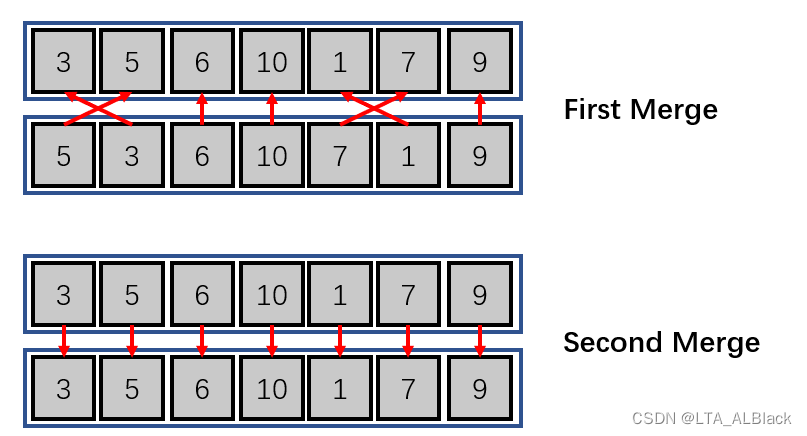
具体怎么捣腾呢?设计循环长度为2数组,利用取余方案进行循环(我们使用tempRow来表示循环指针)
// Step 3. Merge. log n rounds
tempRow = -1;
for (int tempSize = 1; tempSize <= length; tempSize *= 2) {
// Reuse the space of the two rows.
tempRow++;
tempActualRow = tempRow % 2;
tempNextRow = (tempRow + 1) % 2;
//...
}// Of for tempSize 这里可以注意到,代码中设置了一个步长tempSize,其值是1->2->4二倍地增加,这是因为这里的步长代表了我们进行合并时数据的最大长度,基础长度是1,每次俩俩合并,那么下回合基础长度自然是4,如此类推。
tempGroups = length / (tempSize * 2);
if (length % (tempSize * 2) != 0) {
tempGroups++;
} // Of if然后继续在刚刚代码的循环题中的待定区补充如上代码。这个tempGroup表示的含义是当前数组归并为新的数组时成组的个数。以下面的图来说明:
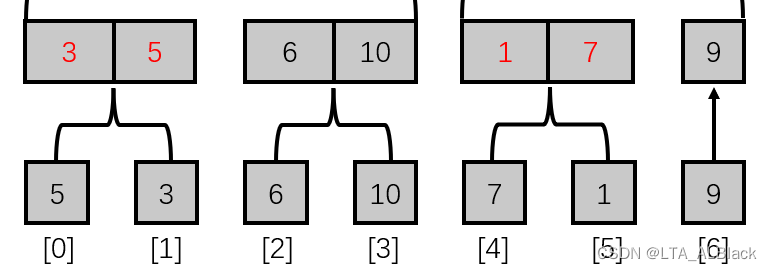
这里最初数组的步长tempSize = 1,俩俩组合后新的数据块大小为tempSize * 2,那么自然数据块的个数就是length / (tempSize * 2)。当然因为整型除法小数点缺失的特性,一旦除法可余我们需要把归并的这个尾巴补上。
for (tempGroupNumber = 0; tempGroupNumber < tempGroups; tempGroupNumber++) {
tempFirstStart = tempGroupNumber * tempSize * 2;
tempSecondStart = tempGroupNumber * tempSize * 2 + tempSize;
if (tempSecondStart > length - 1) {
// Copy the first part.
for (int i = tempFirstStart; i < length; i++) {
tempMatrix[tempNextRow][i] = tempMatrix[tempActualRow][i];
} // Of for i
continue;
} // Of if
tempSecondEnd = tempGroupNumber * tempSize * 2 + tempSize * 2 - 1;
if (tempSecondEnd > length - 1) {
tempSecondEnd = length - 1;
} // Of if
System.out.println("Trying to merge [" + tempFirstStart + ", " + (tempSecondStart - 1) + "] with ["
+ tempSecondStart + ", " + tempSecondEnd + "]");
}// Of for tempGroupNumber
我们继续补上上述代码(为了方便大家明白代码层次,这里分段分享的所有代码都缩进大小都是共享的)。之前之所以确定归并后分块的个数,就是为了确定本回合需要进行归并的次数,于是设置了for循环分别进行执行。
这里关于指针的声明比较麻烦,简单总结来说声明了三个指针:
- tempFirstStart 用来说明二路归并部分中左路数组的初始下标
- tempSecondStart 用来说明二路归并部分中右路数组的初始下标
- tempSecondEnd 用来说明二路归并部分中右路数组的结束下标(闭区间)
用区间表示的话,左路归并数组为\([tempFirstStart, tempSecondStart-1]\),右路归并数组为\([tempSecondStart, tempSecondEnd]\)。若再一个图举例就是:
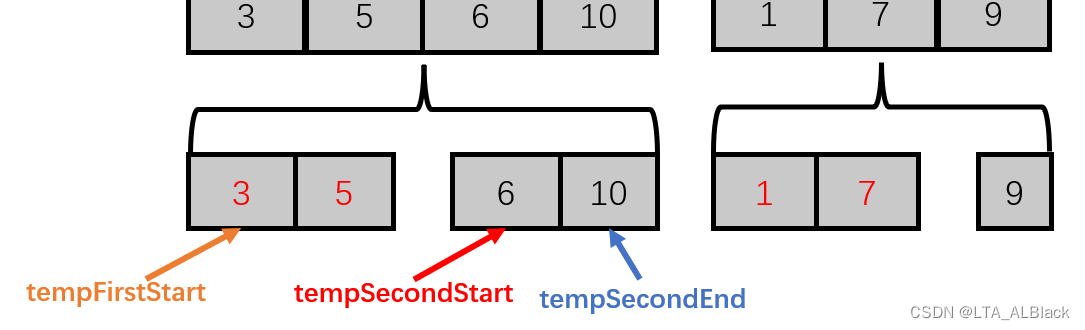
这里为何要用三个指针?首先第一、二个指针是必须的,要说明第一、二个数组序列的开始,这也是为后续进行元素合并做考量的。若我们的归并都是严格的等分的话,那么确实就不需要额外第三个指针了,但是很不幸,归并存在留有尾巴的方案。于是最稳妥的方案,采用地三个指针说明右路数组的结束下标。
其实,归并排序中只要左右路都存在,那么其实任何时刻左路数组的步长应该是确定的,只有右路长度会变化,而且一旦右路不是定长的话,那么右路的最后一个元素的下标一定是length - 1。
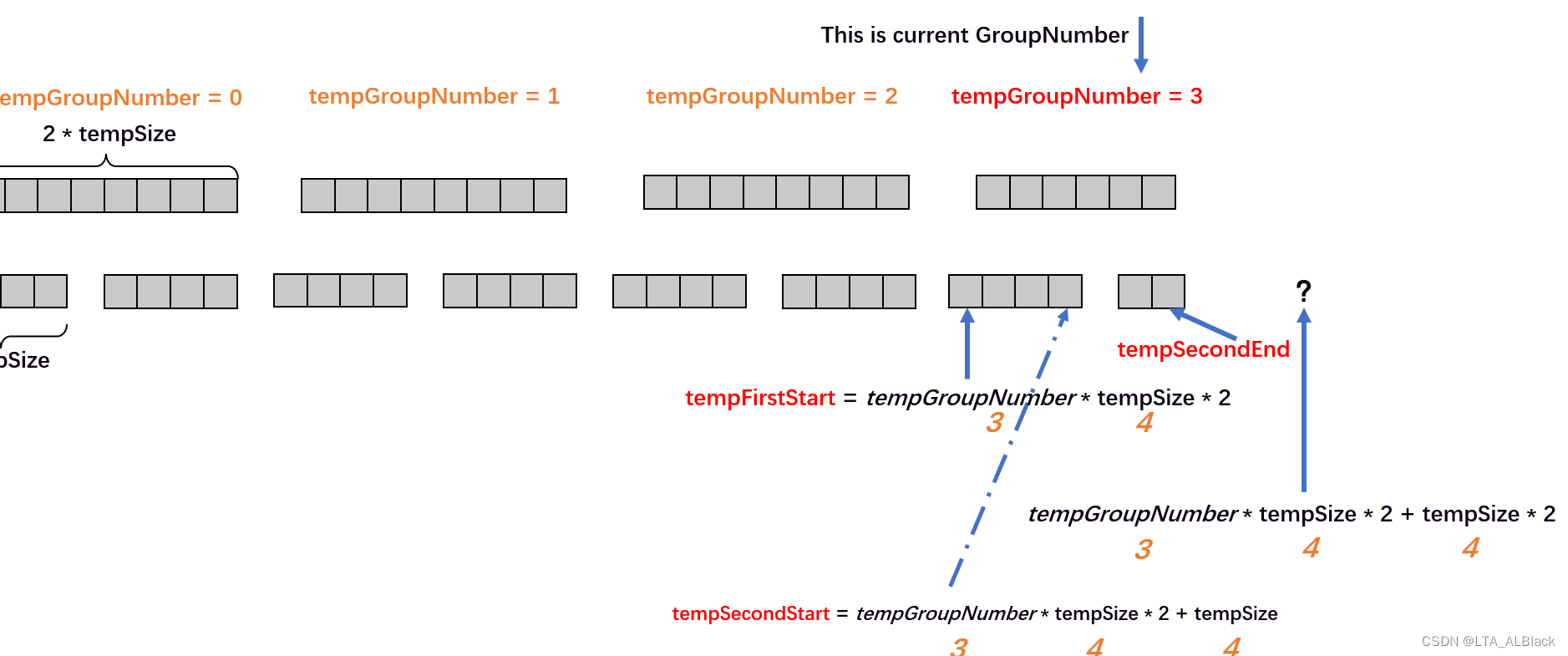
那么这些指针是怎么得到的?如果单纯想而不画图你是几乎无法理解的,但是一画图就会明了起来(见图,为了方便理解,我分别画出了这个指针在原始数据的位置已经在合并后的位置)代码描述为:tempFirstStart = tempGroupNumber * tempSize * 2; 这里的tempGroupNumber表示了合并后的数据块在合并后的数据块中的序号(这里是2),这个序号可以理解为当前数据块前面有多少个数据块,而tempSize * 2恰好是单个数据块的长度(因为tempSize表示的是未合并前的步长),那么这里tempFirstStart就很好说得清了,其表示了当前指针前有多少数据项。再由刚刚得到的两路都在时左路步长确定,自然也不难得出第二个指针为:tempSecondStart = tempGroupNumber * tempSize * 2 + tempSize; (注意我们讨论的下面那层!步长不要*2)
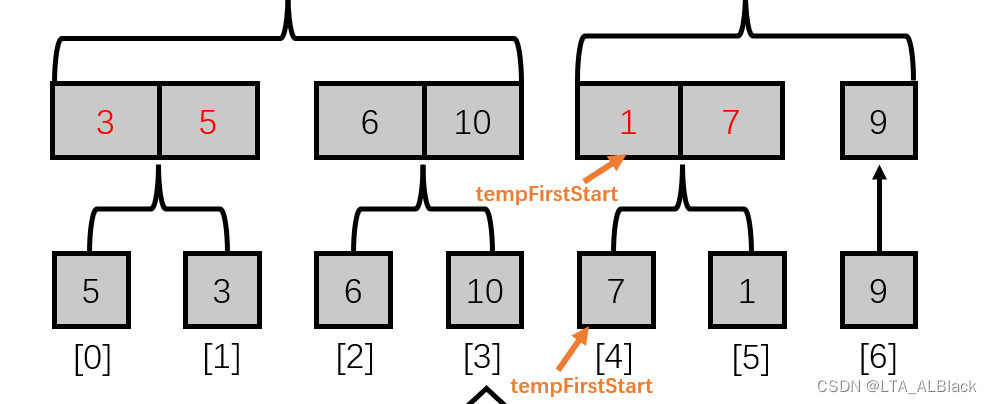
如果tempSecondStart 越界了,那么我们就遇到了右路不存在的情况(见下图)
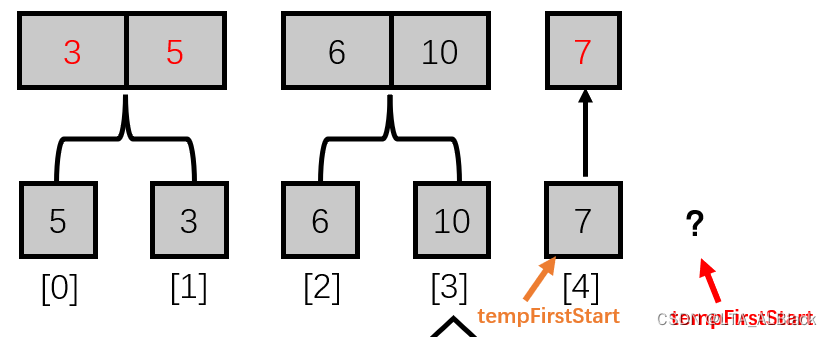
本次合并取消,直接移交到轮换存储器中。
if (tempSecondStart > length - 1) {
// Copy the first part.
for (int i = tempFirstStart; i < length; i++) {
tempMatrix[tempNextRow][i] = tempMatrix[tempActualRow][i];
} // Of for i
continue;
} // Of if后续右路指针的代码为tempSecondEnd = tempGroupNumber * tempSize * 2 + tempSize * 2 - 1; 这里我将其相比tempFirstStart 多出来的地方标记为了绿色。这段tempSize * 2 在于直接跳过当前二路归并的范围,进入下一个二路归并的首指针位置,然后通过-1直接返回到当前二路归并的右路的最后位置。如果还是不理解希望下面这个图能帮你理解。
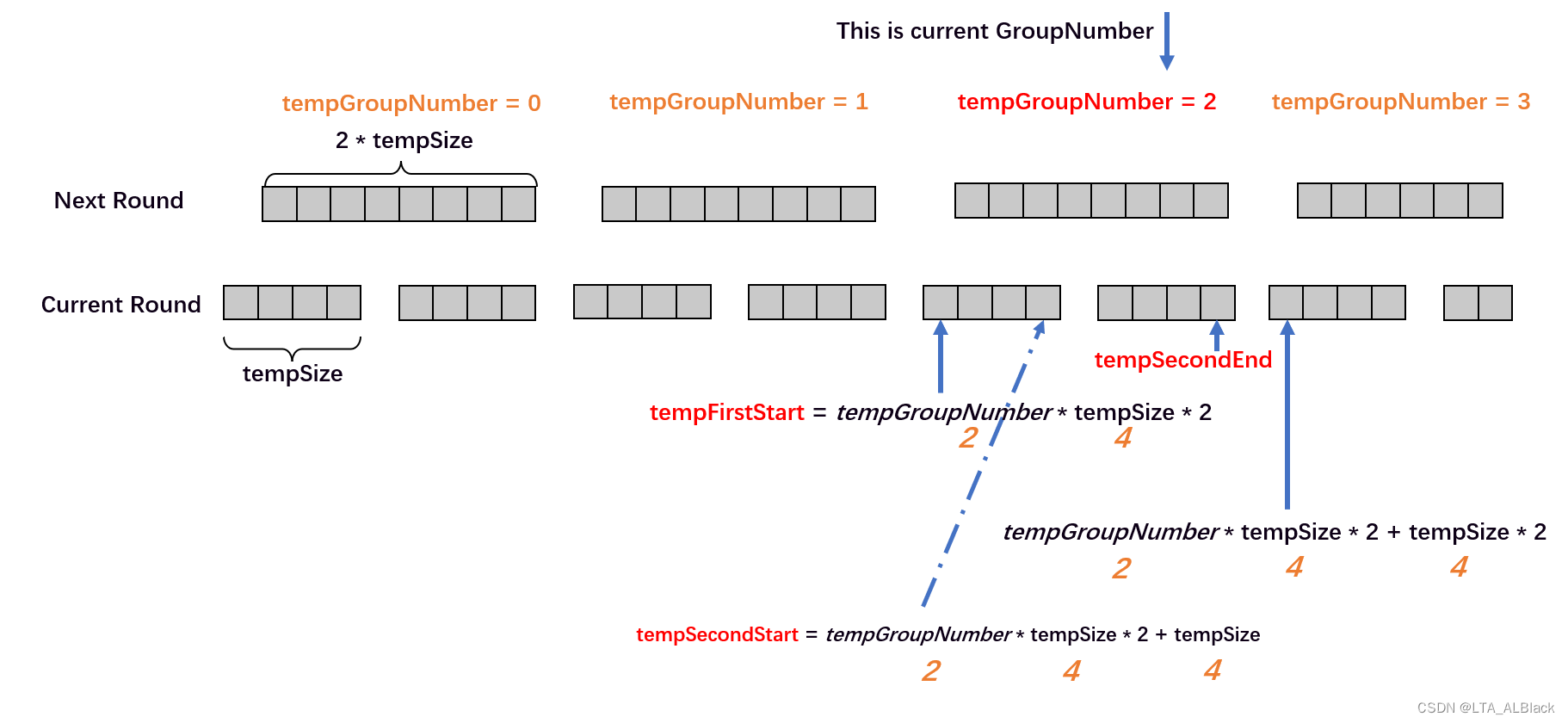
若tempSecondEnd = tempGroupNumber * tempSize * 2 + tempSize * 2 - 1的值越界了呢?那么就直接令tempSecondEnd等于length - 1就好了,见下图:
在完成指针确定后,恭喜你,你已经完成迭代法中初始理解时最麻烦的部分,后面就是通过我们的指针进行数组合并的过程了,这步我默认诸位都是清楚的。这里我贴出全部代码,诸位在搞懂上面的思路后,下面一些数据定义便迎刃而解:
/**
*********************
* Merge sort. Results are stored in the member variable data.
*********************
*/
public void mergeSort() {
// Step 1. Allocate space.
int tempRow; // The current row
int tempGroups; // Number of groups
int tempActualRow; // Only 0 or 1
int tempNextRow = 0;
int tempGroupNumber;
int tempFirstStart, tempSecondStart, tempSecondEnd;
int tempFirstIndex, tempSecondIndex;
int tempNumCopied;
for (int i = 0; i < length; i++) {
System.out.print(data[i]);
} // Of for i
System.out.println();
DataNode[][] tempMatrix = new DataNode[2][length];
// Step 2. Copy data.
for (int i = 0; i < length; i++) {
tempMatrix[0][i] = data[i];
} // Of for i
// Step 3. Merge. log n rounds
tempRow = -1;
for (int tempSize = 1; tempSize <= length; tempSize *= 2) {
// Reuse the space of the two rows.
tempRow++;
System.out.println("Current row = " + tempRow);
tempActualRow = tempRow % 2;
tempNextRow = (tempRow + 1) % 2;
tempGroups = length / (tempSize * 2);
if (length % (tempSize * 2) != 0) {
tempGroups++;
} // Of if
System.out.println("tempSize = " + tempSize + ", numGroups = " + tempGroups);
for (tempGroupNumber = 0; tempGroupNumber < tempGroups; tempGroupNumber++) {
tempFirstStart = tempGroupNumber * tempSize * 2;
tempSecondStart = tempGroupNumber * tempSize * 2 + tempSize;
if (tempSecondStart > length - 1) {
// Copy the first part.
for (int i = tempFirstStart; i < length; i++) {
tempMatrix[tempNextRow][i] = tempMatrix[tempActualRow][i];
} // Of for i
continue;
} // Of if
tempSecondEnd = tempGroupNumber * tempSize * 2 + tempSize * 2 - 1;
if (tempSecondEnd > length - 1) {
tempSecondEnd = length - 1;
} // Of if
System.out.println("Trying to merge [" + tempFirstStart + ", " + (tempSecondStart - 1) + "] with ["
+ tempSecondStart + ", " + tempSecondEnd + "]");
tempFirstIndex = tempFirstStart;
tempSecondIndex = tempSecondStart;
tempNumCopied = 0;
while ((tempFirstIndex <= tempSecondStart - 1) && (tempSecondIndex <= tempSecondEnd)) {
if (tempMatrix[tempActualRow][tempFirstIndex].key <= tempMatrix[tempActualRow][tempSecondIndex].key) {
tempMatrix[tempNextRow][tempFirstStart
+ tempNumCopied] = tempMatrix[tempActualRow][tempFirstIndex];
tempFirstIndex++;
System.out.println("copying " + tempMatrix[tempActualRow][tempFirstIndex]);
} else {
tempMatrix[tempNextRow][tempFirstStart
+ tempNumCopied] = tempMatrix[tempActualRow][tempSecondIndex];
System.out.println("copying " + tempMatrix[tempActualRow][tempSecondIndex]);
tempSecondIndex++;
} // Of if
tempNumCopied++;
} // Of while
while (tempFirstIndex <= tempSecondStart - 1) {
tempMatrix[tempNextRow][tempFirstStart + tempNumCopied] = tempMatrix[tempActualRow][tempFirstIndex];
tempFirstIndex++;
tempNumCopied++;
} // Of while
while (tempSecondIndex <= tempSecondEnd) {
tempMatrix[tempNextRow][tempFirstStart
+ tempNumCopied] = tempMatrix[tempActualRow][tempSecondIndex];
tempSecondIndex++;
tempNumCopied++;
} // Of while
} // Of for groupNumber
System.out.println("Round " + tempRow);
for (int i = 0; i < length; i++) {
System.out.print(tempMatrix[tempNextRow][i] + " ");
} // Of for j
System.out.println();
} // Of for tempStepSize
data = tempMatrix[tempNextRow];
}// Of mergeSort三、单元测试及其结果
/**
*********************
* Test the method.
*********************
*/
public static void mergeSortTest() {
int[] tempUnsortedKeys = { 5, 3, 6, 10, 7, 1, 9 };
String[] tempContents = { "if", "then", "else", "switch", "case", "for", "while" };
DataArray tempDataArray = new DataArray(tempUnsortedKeys, tempContents);
System.out.println(tempDataArray);
tempDataArray.mergeSort();
System.out.println(tempDataArray);
}// Of mergeSortTest演示图
运行结果

性能与特性分析
无论在归并排序的递归算法中还是迭代算法中,每次进行合并的时候都需要利用一个数组部分进行中间存储,所以归并排序的空间复杂度为\(O(N)\)。当我们是讨论的二路归并时由于递归树是一个二叉树,这个二叉树是通过严格二分得到的,因此不同于快排,这里的树高严格是\(logN\)级别的,且每次合并时的复杂度都是\(O(N)\),可以基本地确定二路归并的时间复杂度为不变的\(O(NlogN)\),排序效果与初始状态无关。扩展到其他多路归并,无非是层次减少而合并时判断语句造成的开销变大,复杂度是近似的。
归并排序还有一个高级排序中格外宝贵的特性——归并排序是稳定的!归并排序的元素相对位置取决于合并时两个有序数组中相同元素的处理,这个补充可以非常容易人为代码实现:当两个指针遇到相同元素,默认将左路数组控制指针指向的元素先输入就可以了。这个特性使得稳定排序的适用范围也突破了\(O(N^2)\)的瓶颈。
链表可以用于归并吗?归并排序算法的两个核心:分割与合并。合并即有序表的合并,这个有存储的链表实现方法,而且比顺序表更直观。分割操作需要取中点,这个其实可以通过快慢指针来实现(快指针每次走两步,慢指针每次走一步,当快指针走到底时,慢指针就是中点位置),只不过找中点分割似乎就需要依次循环,但是不用担心的是,这种分割似乎是可预测的单次循环,可以将其与当次的合并复杂度合并为\(O(N)\)。因此,归并对于顺序存储与链式存储都适用。
归并排序无法在排序中途确定任何一个元素的最终位置,这是因为有序数组合并操作会对两个数组的元素都进行重排。
总结
归并排序自底向上的迭代写法确实是第一次尝试写,关于步长分块部分稍微画了图花时间理解了下,懂了后也花时间想了怎么在博客中说清楚这个问题,这就是为什么今天文章发表延期了一天的原因....虽然感觉这样写确实比递归复杂了,但是这种方案对于超大的数据可以避免调用栈的崩溃,也是可取的一种方案。值的一提的一个冷知识,最早冯 · 洛伊曼在1945年提出归并的自顶向下的递归代码后,在1948年还专门与赫尔曼·海因·戈德斯坦发表了一篇论文阐述了这种自底向上的迭代法,关于归并排序的递归法与迭代法这两个思路并不是同一时间诞生的。
其实归并不仅仅用于内部排序,它最伟大之处还是在于其分块合并的思想还为外部排序提供了一种高效的排序方案,算是唯一一个可以兼顾内外排序的一个强大的算法。