注意:这里是JAVA自学与了解的同步笔记与记录,如有问题欢迎指正说明
目录
一、单源最短路径路径问题的解决
1.关于路径问题
最短路径问题(Shortest Path)是图论中至关重要的一系列问题,这类问题来自于现实的各种交通问题,决策问题,通信问题,涉及运筹学信息论等各种方面学科。是图论中最具有价值意义的一部分内容,也是真正会用图论知识去解决实际问题和延展与图相关特性的其他算法的桥梁。这部分涉及的许多算法思想会给许多相关类似的算法带来一定启示。
在这类问题中,我们总是讨论图中某些结点之间在可达的基础上能以预期尽可能最小的权值枚举出最优的路径(边集合)
最短路径中一种比较基础的一类问题就是单源最短路径问题。在这类问题中,我们确定了一个固定的起点,讨论从这个起点到其余顶点的最短路径问题。若针对无权的图结构,可以采用BFS的同步前进的广度特性实现这个过程,保证每部的全枚举。但是针对带权网,这种同步难以实现,需要讨论其余策略。
2.关于Dijkstra算法
1956年,荷兰的计算机学者Edsger Wybe Dijkstra成功地设计并实现了在有障碍物的两个地点之间找出一条最短路径的高效算法,这个算法在后来被命名为“Dijkstra算法”。这个算法对于解决单源最短路径具有出奇的效率,后来作为许多路径算法的基础思想,成为一个关于解决路径问的经典算法,几乎是每个计算机人接触路径问题的,真正意义上的第一个算法。(有兴趣可以去了解下Dijkstra生平和其提出的各种计算机理论,Dijkstra可谓计算机领域的一个传奇大神)
Dijkstra有一些非常显著的特征,其实通过维护一个单源路径数组来构造最短路径问题,并且通过维护逻辑上的集合,实现问题的解决。这是一个关键的思路,也是今日我们介绍这两个算法的桥梁。
下面为了描述好这个算法的过程,可以假设两个辅助数组与一个集合的定义:
- dist[ ]:记录从源点\(v_0\)到其他各顶点的最短路径,其初始态由\(v_0\)的邻边关系确定。倘若存在\(<v_0, v_i>\),则设置dist[i]为此权值,否则设置dist[i] = ∞(这里∞在代码中可以是一个超过接收范围的一个数)
- path[ ]:path[i]表示了从源点到顶点i之前最短路径的前驱结点,假如说path[i]=j,那么就是说明源节点\(v_0\)到\(v_i\)结点的图中最后要经历的结点是\(v_j\),简单来说,这条最短路径可以表示为\(v_0,...,v_j,v_i\)。这个数组可以通过迭代的写法推出全部路径。
- 设置一个集合\(S\)来表示已经求得的最短路径顶点,\(V\)表示全部顶点。假设源点为\(v_0\),默认初始化时\(S\)集合内只有顶点\(v_0\)
确定好这个算法的准备后可以开始进行算法描述:
- 初始化来看,集合\(S = {0}\),\(dist[i] = M[0][i],i=1,2,3,...,n-1\)。注意,这里M表示网的邻接矩阵。
- 选出顶点\(v_j\)满足\(dist[j]=Min \left \{ dist[i]|v_i \in V - S \right \}\),即找到dist[ ]中未纳入\(S\)集合的值对应的下标\(j\),\(v_j\)就是当前求得的一条从\(v_0\)出发的最短路径终点,令\(S = S \cup \left \{ j \right \}\)
- 保留\(v_j\)这个最优结点,遍历集合\(V-S\)得到任意一个顶点\(v_k\),若满足\(dist[j]+M[j][k] < dist[k]\),则更新\(dist[j]+M[j][k] = dist[k]\)。这个过程是Dijkstra算法的核心,我们常称之为松弛。同时更新有\(path[k] = j\)。
- 重复2~3步,一共执行操作n-1次,直到所有顶点都转移到\(S\)中。
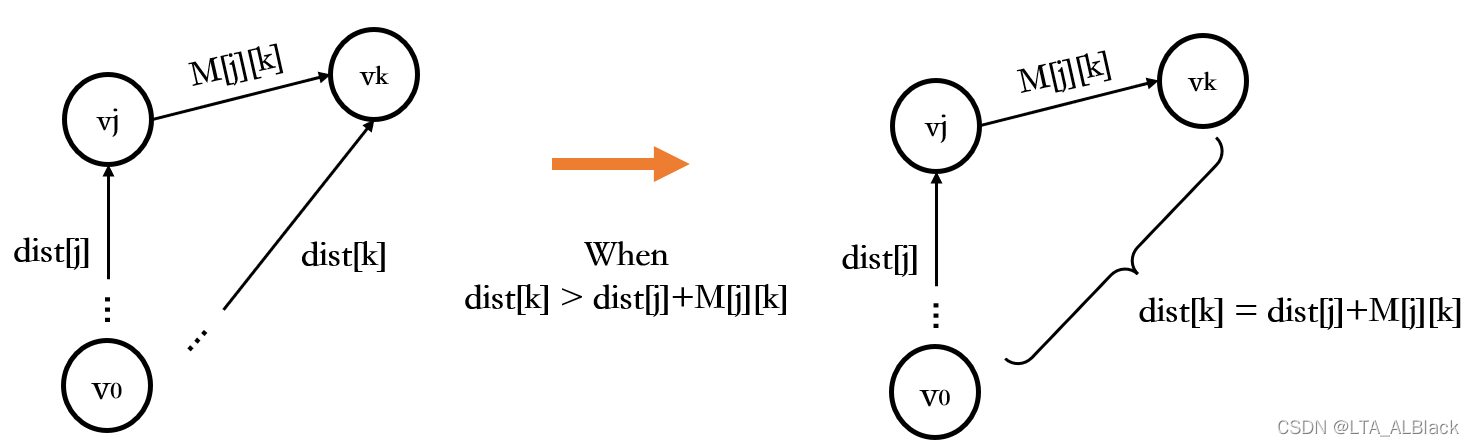
这种松弛过程巧妙之处在于,其通过当前取到的\(v_j\)为基点,讨论了所有集合\(V-S\)内的顶点可松弛的情况。又因为每次取到的\(v_j\)是单源的最优目标点(求的Min()),因此后续松弛的情况一定是基于当前基点的最优而讨论的。因此可以发现我们无论是松弛操作还是选定当前单源最优点我们都是基于当前最小原则。因此可以发现Dijkstra算法采用的也是一种贪心思想。
二、Dijkstra算法的代码实现
1.网状结构的类声明
在编写代码开始前,需要认识到Dijkstra算法本身是基于网状结构的一个算法,它有明显的边权值,这不同于之前我们构造无权图结构:
/**
* The maximal distance. Do not use Integer.MAX_VALUE.
*/
public static final int MAX_DISTANCE = 10000;
/**
* The number of nodes.
*/
int numNodes;
/**
* The weight matrix. We use int to represent weight for simplicity.
*/
IntMatrix weightMatrix;
/**
*********************
* The first constructor.
*
* @param paraNumNodes The number of nodes in the graph.
*********************
*/
public Net(int paraNumNodes) {
numNodes = paraNumNodes;
weightMatrix = new IntMatrix(numNodes, numNodes);
for (int i = 0; i < numNodes; i++) {
// For better readability, you may need to write fill() in class
// IntMatrix.
Arrays.fill(weightMatrix.getData()[i], MAX_DISTANCE);
} // Of for i
}// Of the first constructor
/**
*********************
* The second constructor.
*
* @param paraMatrix The data matrix.
*********************
*/
public Net(int[][] paraMatrix) {
weightMatrix = new IntMatrix(paraMatrix);
numNodes = weightMatrix.getRows();
}// Of the second constructor
/**
*********************
* Overrides the method claimed in Object, the superclass of any class.
*********************
*/
public String toString() {
String resultString = "This is the weight matrix of the graph.\r\n" + weightMatrix;
return resultString;
}// Of toString需要说明一些特别的变量和函数体。这里定义的静态变量MAX_DISTANCE表示无穷大,用于表示算法中的不可达值。在第一个构造函数中,我们默认构造的邻接矩阵中所有初始值都为无穷大,以方便避免在赋值时的额外操作。
2.核心代码
首先完成初始化,这部分可见刚刚的算法过程描述。这里逐一为变量进行翻译:tempDistanceArray 代表dist[ ],分别为其初始化源顶点到各顶点的距离(因为邻接矩阵本身能承载不可达信息,所以统一赋值能兼顾不可达的初始化);tempParentArray代表path[ ]数组,初始为-1表示无路径依赖;tempVisitedArray 是一种标记手段,可以用来表明tempDistanceArray中哪些顶点已经被纳入\(S\)集合。
// Step 1. Initialize.
int[] tempDistanceArray = new int[numNodes];
for (int i = 0; i < numNodes; i++) {
tempDistanceArray[i] = weightMatrix.getValue(paraSource, i);
} // Of for i
int[] tempParentArray = new int[numNodes];
Arrays.fill(tempParentArray, paraSource);
// -1 for no parent.
tempParentArray[paraSource] = -1;
// Visited nodes will not be considered further.
boolean[] tempVisitedArray = new boolean[numNodes];
tempVisitedArray[paraSource] = true;核心的for循环内部的两个for循环本身上就是2、3步骤的循环。第一个for循环中,于\(V-S\)集合中找到一个最小的值的顶点,这个操作通过一个for循环完成,其实就是在tempDistanceArrays数组中找到未被tempVisitedArray标记的最小值。并将最小值统计到tempMinDistance中,将最小值下标统计到tempBestNode 中。然后标记这个下标(这部可以理解为将结\(v_{tempBestNode}\))纳入集合\(S\)中去。
完成第一个for循环之后,我们确定了最优基础点\(v_{tempBestNode}\)后,便依据这个基础点枚举所有集合\(S\)集合内的顶点,逐个讨论松弛可能。
// Step 2. Main loops.
int tempMinDistance;
int tempBestNode = -1;
for (int i = 0; i < numNodes - 1; i++) {
// Step 2.1 Find out the best next node.
tempMinDistance = Integer.MAX_VALUE;
for (int j = 0; j < numNodes; j++) {
// This node is visited.
if (tempVisitedArray[j]) {
continue;
} // Of if
if (tempMinDistance > tempDistanceArray[j]) {
tempMinDistance = tempDistanceArray[j];
tempBestNode = j;
} // Of if
} // Of for j
tempVisitedArray[tempBestNode] = true;
// Step 2.2 Prepare for the next round.
for (int j = 0; j < numNodes; j++) {
// This node is visited.
if (tempVisitedArray[j]) {
continue;
} // Of if
// This node cannot be reached.
if (weightMatrix.getValue(tempBestNode, j) >= MAX_DISTANCE) {
continue;
} // Of if
if (tempDistanceArray[j] > tempDistanceArray[tempBestNode] + weightMatrix.getValue(tempBestNode, j)) {
// Change the distance.
tempDistanceArray[j] = tempDistanceArray[tempBestNode] + weightMatrix.getValue(tempBestNode, j);
// Change the parent.
tempParentArray[j] = tempBestNode;
} // Of if
} // Of for j
// For test
System.out.println("The distance to each node: " + Arrays.toString(tempDistanceArray));
System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
} // Of for i
// Step 3. Output for debug.
System.out.println("Finally");
System.out.println("The distance to each node: " + Arrays.toString(tempDistanceArray));
System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));三、最小生成树问题的解决
1.关于最小生成树
记住上述单源最短路径问题中Dijkstra算法的特性,我们进一步趁热打铁,来描述下Prim算法的过程。
何为生成树,其实这个概念可以有很多中解释。首先,树是不存在环的,你可以认识将一个连通图的所有环破掉,在保证连通的不变的情况下构成的图结构就是生成树(生成树往往是基于无向图的),或者说保留原图的所有顶点而去掉所有边,再在保证连通的情况下逐一添加边(这个是最小生成树之Kruskal算法的思想),再或者最简单的一种理解:对这个图进行遍历的路径构成的树形结构,无论其是BFS树还是DFS树。自然通过这种解释我们也能理解到生成树的一个特性,因为遍历时选择边的差异性,导致图遍历往往不是唯一的,所以生成树也不是唯一的。
因为生成树的不唯一性,从而提出了权值(边权和)最小的生成树——最小生成树(MST:
Minimum Spanning Tree)的概念。最小生成树可以引用于部分图有关最优图组合的问题,常常与并查集等相关方法同时出现,是一种关键的图连通性问题。目前主流的解决最小生成树的算法有Prim算法与Kruskal算法,其分别适用于稠密图与稀疏图等不同情形。
2.关于Prim算法
Prim通过构建一个抽象的生成树集合,并且通过不断遍历原图结构,按照最小边的原则逐步扩充这个生成树的连通点集从而逐步构造一个最小生成树的算法。这种算法分别在上个世纪30年代和50年代被三个人发现,我们现在所谓的Prim算法之名是来自于1957年独立发现这个解法的Robert C. Prim。通过刚刚分析可以发现Prim算法有类似于Dijkstra算法的抽象集合概念与选最优边的特性,这两个相似的算法分别诞生于上个世纪50年代那个计算机领域咆哮的年代,可见这种思路在最初被Edsger Wybe Dijkstra的发掘后不断在计算机邻域的影响力与给其余问题的解决带来的启示。
具体来看下这个算法的流程,更深刻来体会其与Dijkstra的相似性。首先地,假设\(G=\left \{ V,E\right \}\)是一个连通图,先有最小生成树有\(T=( U,E_T)\),\(E_T\)是最小生成树中边的合集,同理与Dijkstra算法的思想,我们的目的是逐步扩展这个集合\(U\)以达到\(U=V\)。
- 初始化:在图\(G\)中确定一个初始结点\(u_0\)加入到集合\(U\)之中,有\(U=\left \{ u_0 \right \}\),\(E_T = \varnothing\)。
- 从图\(G\)中选择一个顶点\(v\),从生成树\(T\)中选择一个顶点\(u\),同时保证存在最小的无向边\((u,v)\)满足\(\left \{ \left ( u,v \right )|u \in U,v\in V-U \right \}\)。
- 将边加入生成树\(T\),设置\(U = U\cup \{ v \} \),\(E_T = E_T\cup \{ (u,v) \} \)。
- 重复2,3步一共\(n-1\)步,或者说直到\(U=V\)。
例如下图中颜色标记的就是小生成树有\(T=( U,E_T)\),而全图为图\(G\)。(这里为方便尚未标注下图权值)
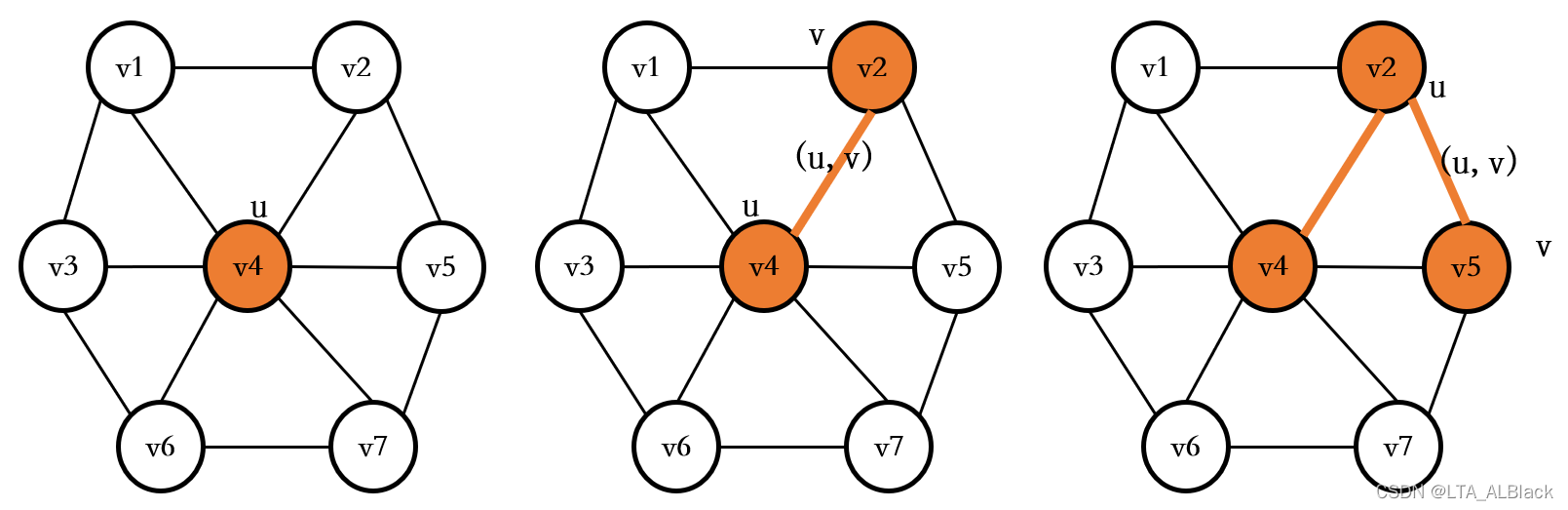
实际在实现的过程中,我们依旧可以采用一个数组来模拟当前进入生成树的结点,只不过其含义就不再是“单源结点到某个顶点的最短距离”了,而是“集合\(V-U\)中的顶点到集合\(U\)的距离情况,具体来说,dist[j]表示为集合\(U\)到\(v_j\)的最短距离”。其实这个距离情况潜藏了一个松弛过程:假如上图\(v_4\)到\(v_7\)的距离为\((v_4, v_7)\),但是通过Prim算法的选择,集合\(U\)扩展到\(v_5\)了,于是通过以\(v_5\)为基点,看它能否对周围的边进行松弛更新。若这时有\((v_5, v_7) > (v_4, v_7) \)(假设其他顶点到\(v_7\)足够远),那么集合\(U\)到\(v_7\)的距离变得更近了,从最开始的dist[7] = \((v_4, v_7)\)变为dist[7] = \((v_5, v_7)\)。
这样的一个数组初始情况下只能连接其邻接边,未接入的边通过Prim算法的逐步向外扩张来实现。这个初始情况与Dijkstra的dist[ ]惊人地一致。
四、Prim算法的代码实现
1.基本初始化
这里的初始化与Dijkstra算法是一模一样的,只不过含义上有所区分。tempDistanceArray表示MST结点集合\(U\)到非子树结点的距离集合,有效下标与非MST结点相关;若有结点\(v_i\)在tempVisitedArray内被标记了说明此结点已经进入MST结点集合\(U\),每次讨论tempDistanceArray时不考虑这些被标记的点。tempParentArray的功能依旧与Dijkstra算法中的path类似,但在MST结构中,这个数组会更有用一些。因为这个数组可以记录结点的父节点,因此可以通过这个操作来查找公共根,或者说,它就是这个MST的树形存储结构(双亲表示法)。这个数组在并查集算法中将非常有用。
// Step 1. Initialize.
// Any node can be the source.
int tempSource = 0;
int[] tempDistanceArray = new int[numNodes];
for (int i = 0; i < numNodes; i++) {
tempDistanceArray[i] = weightMatrix.getValue(tempSource, i);
} // Of for i
int[] tempParentArray = new int[numNodes];
Arrays.fill(tempParentArray, tempSource);
// -1 for no parent.
tempParentArray[tempSource] = -1;
// Visited nodes will not be considered further.
boolean[] tempVisitedArray = new boolean[numNodes];
tempVisitedArray[tempSource] = true;2.核心代码
核心部分与Dijkstra是类似的但是还是有些地方要说明下。
第一个for循环通过找最小值找到基点\(v_{tempBestNode} \),并于tempVisitedArray之中标记这个点,以表示已纳入生成树的结点集\(U\)。后续的for循环目的在于依次筛选集合\(V-U\)内的结点,并且查看这些结点在tempDistanceArray中的距离信息是否可以通过\(v_{tempBestNode} \)结点来松弛。这里松弛的算法基于的是生成子树的顶点组成的整体到非子树部分的距离,而不是最初选择的源结点到这些结点的距离,因此松弛的条件式并不一致,这也是Prim与Dijkstra最核心的差异。这里可以发现,Prim每次选择基点依旧是最短边,而且松弛是也是基于当前相连的顶点中的最短原则,所以Prim也是基于贪心思想的。
// Step 2. Main loops.
int tempMinDistance;
int tempBestNode = -1;
for (int i = 0; i < numNodes - 1; i++) {
// Step 2.1 Find out the best next node.
tempMinDistance = Integer.MAX_VALUE;
for (int j = 0; j < numNodes; j++) {
// This node is visited.
if (tempVisitedArray[j]) {
continue;
} // Of if
if (tempMinDistance > tempDistanceArray[j]) {
tempMinDistance = tempDistanceArray[j];
tempBestNode = j;
} // Of if
} // Of for j
tempVisitedArray[tempBestNode] = true;
// Step 2.2 Prepare for the next round.
for (int j = 0; j < numNodes; j++) {
// This node is visited.
if (tempVisitedArray[j]) {
continue;
} // Of if
// This node cannot be reached.
if (weightMatrix.getValue(tempBestNode, j) >= MAX_DISTANCE) {
continue;
} // Of if
// Attention: the difference from the Dijkstra algorithm.
if (tempDistanceArray[j] > weightMatrix.getValue(tempBestNode, j)) {
// Change the distance.
tempDistanceArray[j] = weightMatrix.getValue(tempBestNode, j);
// Change the parent.
tempParentArray[j] = tempBestNode;
} // Of if
} // Of for j
// For test
System.out.println("The selected distance for each node: " + Arrays.toString(tempDistanceArray));
System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
} // Of for i
int resultCost = 0;
for (int i = 0; i < numNodes; i++) {
resultCost += tempDistanceArray[i];
} // Of for i
// Step 3. Output for debug.
System.out.println("Finally");
System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
System.out.println("The total cost: " + resultCost);五、数据模拟与运行测试
1.Dijkstra算法
代码:
int[][] tempMatrix1 = { { 0, 9, 3, 6 }, { 5, 0, 2, 4 }, { 3, 2, 0, 1 }, { 2, 8, 7, 0 } };
Net tempNet1 = new Net(tempMatrix1);
System.out.println(tempNet1);
// Dijkstra
tempNet1.dijkstra(1);构造的完全图:
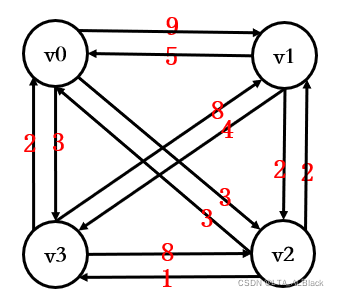
输出信息:

2.Prim算法
代码:
// An undirected net is required.
int[][] tempMatrix2 = { { 0, 7, MAX_DISTANCE, 5, MAX_DISTANCE }, { 7, 0, 8, 9, 7 },
{ MAX_DISTANCE, 8, 0, MAX_DISTANCE, 5 }, { 5, 9, MAX_DISTANCE, 0, 15, },
{ MAX_DISTANCE, 7, 5, 15, 0 } };
Net tempNet2 = new Net(tempMatrix2);
tempNet2.prim();数据图与构成最小生成子树的结果图:
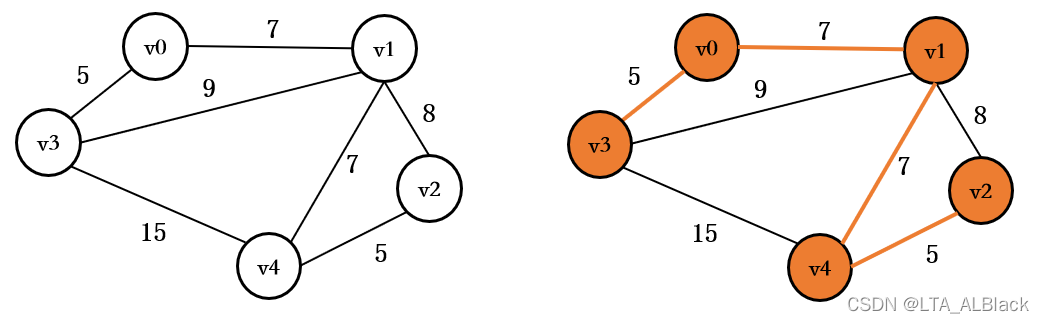
输出数据核对:
MST的权值为24符合预期。双亲表示数组符合树的结构,距离数组可通过手动模拟符合预期。

六、总结
今天这两个算法具有相当的相似性,它们统一地都是将问题划分为一个集合整体更新操作,比如Dijkstra认为构成了最短路径的所有顶点构成了一个集合,并不断从这个集合外选出最优(这里用了贪心)作为松弛的基点,然后在松弛过程中维护距离数组;而Prim也是认为构成MST的所有顶点构成了一个集合,并不断从这个集合外中选出最优(这里还是用了贪心)作为松弛的基点,然后在松弛过程中维护距离数组。唯一不同的就是前者的距离数组表意为源点到每次选点的最短距离,而后者的距离数组表意为整个MST到每次选点的距离,而这个差异也直接导致了它们松弛的条件语句差异。
将原问题转换为集合扩充问题,并且在扩充时基于某种贪心的原则选择局部最优。我们在前几周的Huffman算法中也是采用这种类似的思想,只不过今日的图论与这种思想的结合过程中融合了松弛等较难的思维,但是究其本质是一类贪心算法。所以,其实数据结构很多算法,也许你乍一看或者在初学时感觉他们天差地别,但是当你学习到后续的时候你会逐渐发现他们有些内核是一致的。发现这样的内核有什么用呢?有!这种内核构成问题之间的桥梁,一个非常难的算法可以联想其同内核的简单同类问题,通过分析同类问题的优化策略可以反推得到原来那个非常困难问题的优化思路。
比如我们在Huffman那部分讲到了利用堆排序可以将Huffman的选择最小结点的时间复杂度从\(O(N)\)优化到\(O(logN)\)。同理,Dijkstra算法也可以把集合外的所有结点构建成一个堆,Prim算法中,可以将所有与MST相连的非MST结点构成边建立成一个堆。因为今天内容已经够多了,这里就不展示优化的代码了,总而言之,通过堆的维护,可以保证每次选松弛点的复杂度可以稳定到\(O(logN)\),整体的复杂度可以从\(O(N^2)\)优化到\(O(NlogN)\)(算法复杂度的更标准内容见解详见评论)。另外,对于顶点多边少的情况还可以采用邻接表继续优化....
总之,要找到问题的优化思路,不要死扣问题本身,而是试着找到相似内核的问题。这是个不错的策略,因为同类问题的优化总存在相似性。