注意:这里是JAVA自学与了解的同步笔记与记录,如有问题欢迎指正说明
目录
一、关于堆排序
堆排序是基本的排序算法体系,也就是本科阶段基本要求掌握的算法体系中,是最麻烦的一个算法,因为其涉及了一个全新的数据结构——堆(Heap)。因此在完成堆排序操作时,还需要花费一定操作去维护这个数据结构,但是得到的复杂度代价是理想的,堆排序同样具有同其他高级排序一致的\(O(logN)\)级的复杂度,而且这个复杂度不会收到数组本身情况的影响,是一个状态稳定的复杂度,而且有所有高级排序中最优秀的原地工作的空间开销。
斯坦福大学计算机科学系教授罗伯特·弗洛伊德(Robert W.Floyd)和威廉姆斯(J.Williams)在1964年共同发明了这个完美的算法,并且通过这个排序算法提出了堆这种对后世算法改进影响巨大的数据结构。你可能看到罗伯特·弗洛伊德这位教授的名字有些熟悉?没错,最短路径的Floyd算法正是出自他之手。当然更令人惊奇的是,这位计算机大师曾经竟然是一个文科生?(看看下图这个文质彬彬的大胡子年轻人)

我这里引用相关文章来对于他身世做下描述,让大家体会这个“ 文科 ”计算机大师的故事
年轻的罗伯特·弗洛伊德本来是在芝加哥大学读的文学,后来因为苦于找不上工作,改行去西屋电气公司当了二年计算机操作员,发现他对计算机非常感兴趣。
于是他下定决心要弄懂它,掌握它,于是他借了有关书籍资料在值班空闲时间刻苦学习钻研,有问题就虚心向程序员请教。白天不值班,他又回校去听讲有关课程,逐渐从计算机的门外汉变成计算机的行家里手。
1956年他离开西屋电气公司,到芝加哥的装甲研究基金会(Armour Research Foundation),开始还是当操作员,后来就当了程序员。1962年他被马萨诸塞州的Computer Associates公司聘为分析员,而就在成为分析员的第三年,他就与威廉姆斯共同发表了堆排序的论文,成为继快排后的又一个高级排序。1965年他应聘成为卡内基—梅隆大学的副教授,3年后转至斯坦福大学,1970年被聘任为教授。他的贡献并不止步于堆排序,此外还有直接以Floyd命名的求最短路的算法,这是弗洛伊德利用动态规划原理设计的一个高效算法。同时,他在斯坦福聘任为教授的期间还完成了ALGOL 60编译器开发。弗洛伊德优化编译的思想对编译器发展产生了深刻的影响。随后他又对语法分析进行系统研究提出优先文法、限界上下文文法。
介于其对于计算机领域的突出贡献,最终其与1978年获得图灵奖。
二、堆积树——堆(Heap)结构
既然要解释堆排序,我们就必须要说清楚这个堆结构。堆这个结构非常类似于我们的树形结构,更直观来说,堆结构就是一种基于树形逻辑结构的物理线性结构。为何这个结构能兼容树形又能兼容线性?其实我们在树的那一大板块的开始(21~24天的内容)已经非常明确说明,顺序表可以通过压缩存储来表示一颗二叉树,更好的情况下,如果树是一颗完全树的话,甚至不用压缩存储。因此,给你一个线性顺序表,你可以就把它认为是一个线性表,去表示各形各色的线性结构;此外,你也可以将其顺序分层叠放,将其看作为一个完全二叉树。前者体现物理特性,而后者体现人为的逻辑抽象,为何要这么做呢?因为建立一个树形的逻辑抽象可能将数据的比较上升一个维度,从而发现单独的线性结构所无法轻易发现的特性。
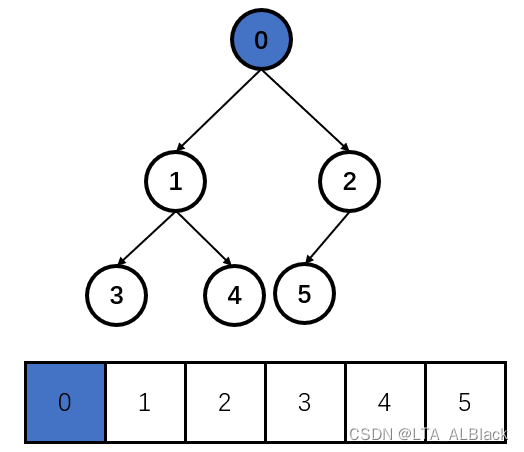
当然,为了严谨起见,我还是要说明一下!并不是所有堆都是完全二叉树,堆不一定是完全二叉树,只是为了方便存储和索引,我们通常用完全二叉树的形式来表示堆,事实上,广为人知的斐波那契堆和二项堆就不是完全二叉树,它们甚至都不是二叉树。下面为了解释方便,本文所描述的堆都是本科基础介绍过的形如完全二叉树结构的一种逻辑结构。

那么在明白这个基本特点之后,我们便来看看逻辑上将线性表抽象为完全二叉树之后可以发现什么特性。首先一点,也是我们在之前学习树的转储时了解的特性,这里再度温习一下:
若用线性结构表示树的话会有一些优良的特性,首先,若下标从0开始算的话,线性抽象的树的某个结点\(i\),其左儿子若存在的话的下标一定是\(2 * i + 1\),其左儿子若存在的话的下标一定是\(2 * i + 2\),父级结点下标一定是\(\left \lfloor \frac{i-1}{2} \right \rfloor\);若下标从1开始的话,左儿子是\(2 * i\),右儿子是\(2 * i + 1\),父亲下标是\(\left \lfloor \frac{i}{2} \right \rfloor\)。这个特性是堆实现目标的基础。
进一步,堆并不是说就是一个单纯的完全二叉树,在堆中存在明显的上下关系。例如大根堆,我们要求树中每个父亲都必须比自己的任何孩子都要大,而孩子之间并不要求大小关系。小根堆则反之。
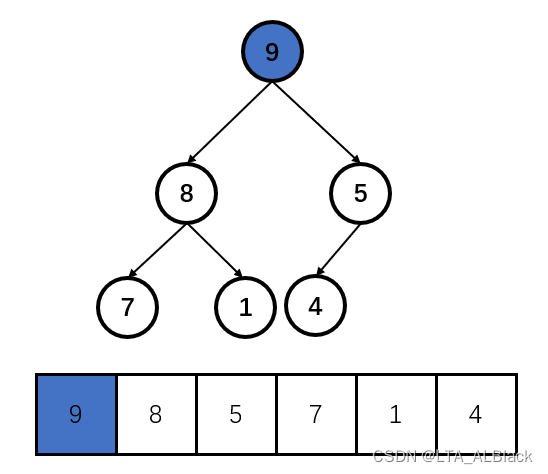
· 创建型堆的维护
堆结构创建往往来说是从一般的线性结构演变而来,毕竟我们往往得到的数据是混乱的,需要在这些数据构成无需无意义的线性结构之后再其维护为一个基于树形结构呈现堆特性的线性表。(这里要反复记住!堆的存储结构是线性的,只是逻辑抽象为一颗完全二叉树而已)
因此,堆的维护就是堆的一个基础特性。以大顶堆为例,算法将堆的维护分割为若干次大数上移操作过程,我们称之为单次向下探测过程。为何明明是大数上移,为何又叫做向下探测呢?因为我们指针在这个过程中其实是在不断向下移动的,这是探测特性;而这个过程中遇到大小不符合大顶堆特性的父子就会发生交换,这个过程中呈现出来的特性就是大的元素上移。
具体的单次向下探测过程:每次进行探测都以一个顶点开始,从顶点向下单向延伸,延伸的过程完成交换操作。我们以下面这个堆的右子树为例。
设置右子树的根为核心结点tempNode,然后再两个儿子结点中找到一个最大的结点,并且与这个最大的儿子结点交换(如下图)
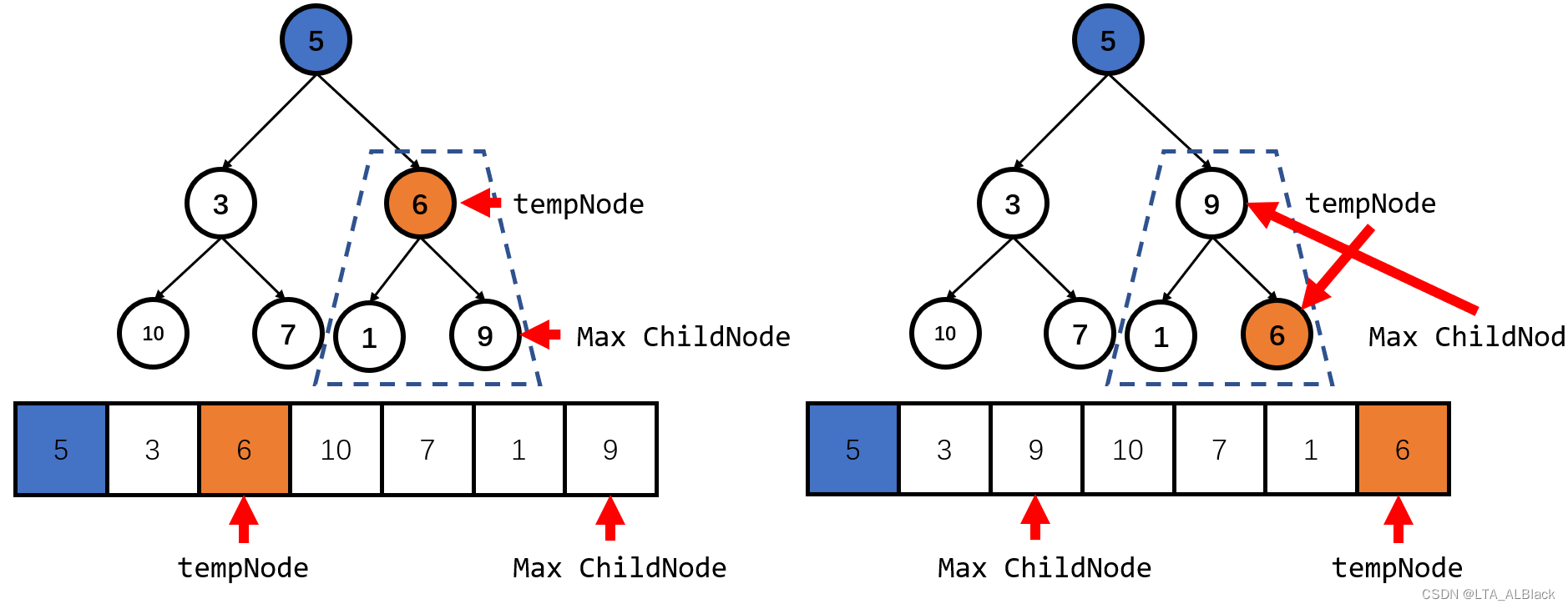
这时候设置新交换tempNode结点,也就是原本的儿子结点,而如今是tempNode的位置为新结点,并以这个结点为根,继续向下探测。上图因为指针指向的位置已经是最后一个元素,故无法继续探测了。
以上就是单次探测的含义。明白这点后,思考单次探测足够了吗?要怎么去运用这次单次探测?通过下图的基于更结点的一次探测维护,可以明显发现,这样的探测仅仅能把根节点放到某个合适的位置,但是这时堆内仍然有大量的元素没在自己合适的位置。
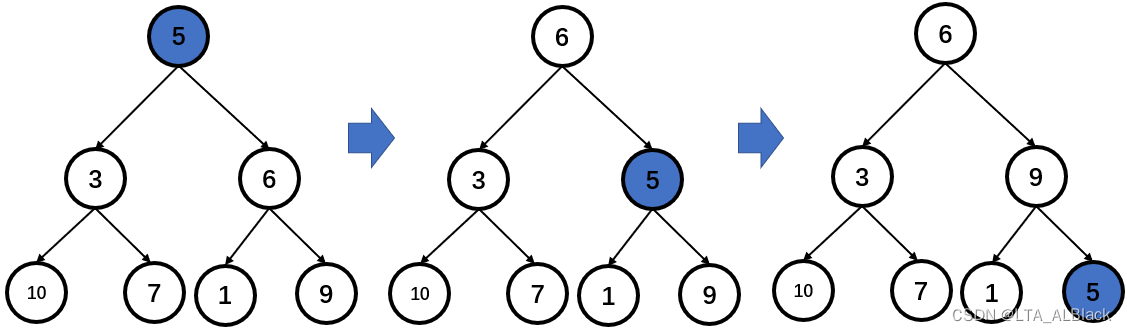
也许自顶向下的思路不可取,我们试着自底向上的思路。自顶向下的思路不可取的原因很大程度是因为与根比对的左右儿子根本无法代表左右子树的最佳情况,准确来说,只有根比对的左右儿子分别是左右子树最大的结点才有意义。而左/右子树自己也是这么认为的,左/右子树的根节点认为,只有本子树的左右儿子能分别代表本子树的左子树的最佳情况和本子树的右子树的最佳情况,那么本子树的调整才有意义!可见,上方的维护都是寄希望于底层的完善性,于是,不如试着从底向上维护,于是我们有这样的定义:从最后一个分支结点开始,自下而上地遍历,每次遍历的时候都以当前选中的分支结点为进行探测的初始结点而进行探测。下图所示模拟。
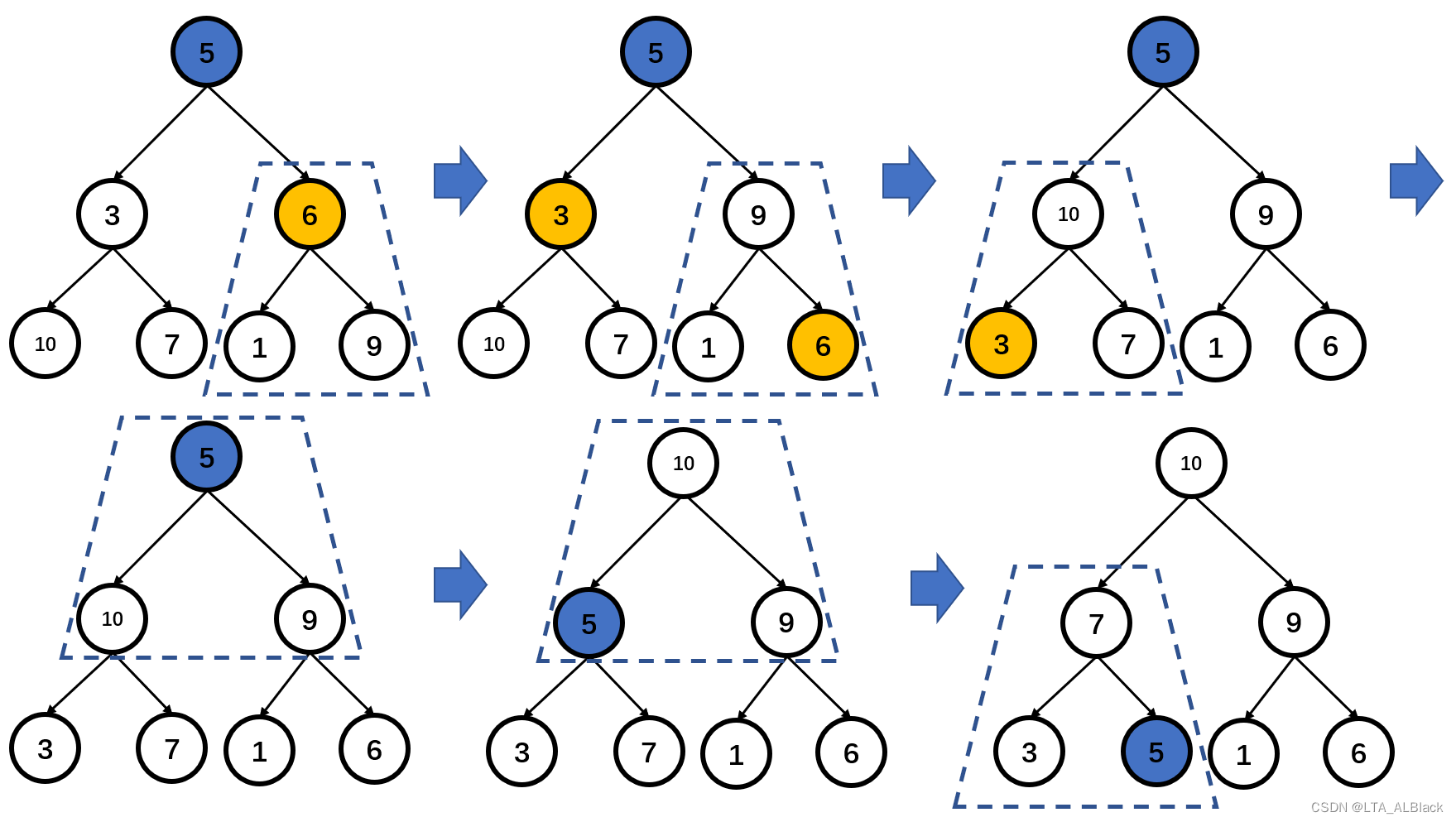
先针对结点为6的分支子树向下探测;再针对结点为3的分支结点向下探测;最后针对根节点向下探测。
· 创建型堆的维护的代码
单次地探测用代码体现出来就是:
/**
*********************
* Adjust the heap.
*
* @param paraStart The start of the index.
* @param paraLength The length of the adjusted sequence.
*********************
*/
public void adjustHeap(int paraStart, int paraLength) {
DataNode tempNode = data[paraStart];
int tempParent = paraStart;
int tempKey = data[paraStart].key;
for (int tempChild = paraStart * 2 + 1; tempChild < paraLength; tempChild = tempChild * 2 + 1) {
// The right child is bigger.
if (tempChild + 1 < paraLength) {
if (data[tempChild].key < data[tempChild + 1].key) {
tempChild++;
} // Of if
} // Of if
System.out.println("The parent position is " + tempParent + " and the child is " + tempChild);
if (tempKey < data[tempChild].key) {
// The child is bigger.
data[tempParent] = data[tempChild];
System.out.println("Move " + data[tempChild].key + " to position " + tempParent);
tempParent = tempChild;
} else {
break;
} // Of if
} // Of for tempChild
data[tempParent] = tempNode;
System.out.println("Adjust " + paraStart + " to " + paraLength + ": " + this);
}// Of adjustHeap这部分用代码能加强单次我们对于单次探测的理解。我们用tempParent记录下父亲结点的下标;tempKey记录下父级结点的值以便于后续的比较;并用tempNode记录下父级结点的整个对象,当然我希望读者不要仅仅将其认为是父级结点对象,而应当将其理解为某个结点的暂存区。因为这样大家更好理解我们为什么这么做:因为单次探测说白了其实就是进行交换和不进行交换两种情况,我们懒得讨论最后是否真的交换或没交换以至于设置一大堆条件来判断判断。于是不如将父级结点先放到暂存区,无论最后是否真的交换,我们都将暂且区tempNode的数据放到data[tempParent](tempParent受交换发生或者不发生影响)。
DataNode tempNode = data[paraStart];
int tempParent = paraStart;
int tempKey = data[paraStart].key;后续代码以孩子结点的指针tempChild为工作指针不断向下探测,每次我都默认探测左孩子,如此而来不断向下单向地单词地深度遍历。这个过程要明白其物理结构本质是线性的,故要合理利用线性树的\(2 * i + 1\)特性来遍历,并且注意越界。
for (int tempChild = paraStart * 2 + 1; tempChild < paraLength; tempChild = tempChild * 2 + 1) {
// ...
} // Of for tempChild第一个条件语句用于判断左右孩子哪个大?并将tempChild指向最大的那个。因为我们的遍历是默认遍历左儿子,所以tempChild最开始都是指向左儿子,所以你可以认为这里默认左儿子最大,通过比较之后发现右儿子更大,故通过tempChild++ 指向右儿子。
// The right child is bigger.
if (tempChild + 1 < paraLength) {
if (data[tempChild].key < data[tempChild + 1].key) {
tempChild++;
} // Of if
} // Of if第二个条件语句就是最大的孩子与父级相比谁大。若孩子更大,通过操作data[tempParent] = data[tempChild];将父级对象修改为孩子的值,实现大数上移;并且通过tempParent = tempChild;实现父级指针下移,为下次探测做准备,同时tempParent值的改变也说明本次交换成立。可见这一个对象交换,一个指针下移,分别诠释了大顶堆调整过程中大数上移,向下探测两个思路。
if (tempKey < data[tempChild].key) {
// The child is bigger.
data[tempParent] = data[tempChild];
System.out.println("Move " + data[tempChild].key + " to position " + tempParent);
tempParent = tempChild;
} else {
break;
} // Of if
} // Of for tempChild如果交换发生,我们将暂存区的数据放到本次探测交换后的儿子结点中(下次探测的父级)。如果交换没发生,那么老老实实交付交换后的父亲结点。代码就是一句。
data[tempParent] = tempNode;
以上就是单次探测的代码,我们将其封装到函数adjustHeap函数中。于是可通过我们上面分析的自底向上方式,分别遍历分支结点,完成完整的对堆维护的代码。(技巧:从0为下标开始的线性结构逻辑抽象为完全二叉树后,若线性表长度为\(n\),那么\(\left \lfloor \frac{n}{2} \right \rfloor - 1\)恰好就是最后一个分支结点的下标,这个是由完全二叉树中叶子节点个数比双分支结点多一个的特性而确定的)
// Step 1. Construct the initial heap.
for (int i = length / 2 - 1; i >= 0; i--) {
adjustHeap(i, length);
} // Of for i· 添加型堆维护
关于堆的维护其实不只在创建时进行全局性的维护,对堆元素的更新优化也是维护堆需要考虑的事情,而这部分内容是堆之所以能应用于贪心的优化(前几日我们关于Dijkstra,Prim,Huffman tree的优化所采用的堆)的原因。下面分别讲述下添加元素与删除元素的基本操作。
我们将上面维护完成的堆结构拿下来。若是元素插入,首先先将元素自然地添加到顺序表的末尾,体现在逻辑的树当中就是层次遍历顺序地添加到最后:
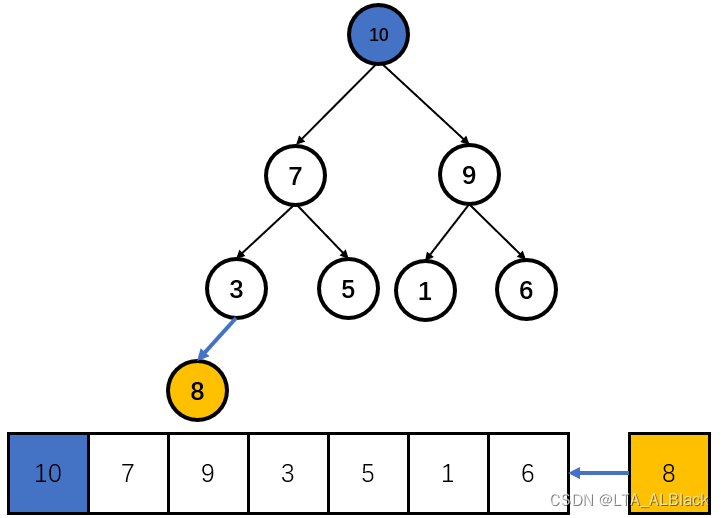
然后我们从插入节点所在的那颗子树开始逐步向上探测,并且维护堆的特性。这个过程不同于创建时的维护,这个过程我们只需要将目光投入到插入结点向上移动的过程,因此这个操作是非常方便且快捷的,总的来看只需要\(O(logN)\)的复杂度就可以确定当前数组的最大元素,这就之前贪心优化中将\(O(N)\)优化为\(O(logN)\)的根源。
因此这个方法作为优化的辅助工具是很方便。因为假若数组初始是空的,可以逐步通过这种添加的方案慢慢维护为一个堆结构,而不是先确定一个乱序的数组,再对这个数组进行维护。因此对于某些在早期不确定添加的全部数据内容的算法,这种结构可以逐步随着算法的延展而辅助延展,成为算法的中间一步。
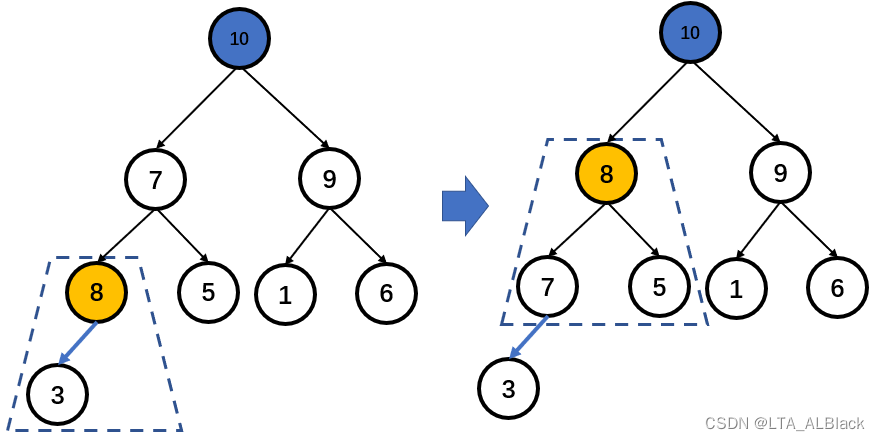
添加操作的代码是一种向上探测,这与我们设计adjustHeap函数的向下探测是相违背的,因此需要设计一个专门的代码来实现。介于我们在堆排序中并不会实际使用到这种方法,我们就不赘述其代码,有兴趣的读者可以试试,并不难哟。
· 删除型堆维护
堆的删除操作比较特别,因为堆总是维护堆顶元素的极值特性,所以堆的删除操作只能删除堆顶元素,我们往往习惯称之为弹出堆顶元素。在操作时,将堆顶元素与数组结构的最后一个元素交换,并且删除末尾元素。具体见图:
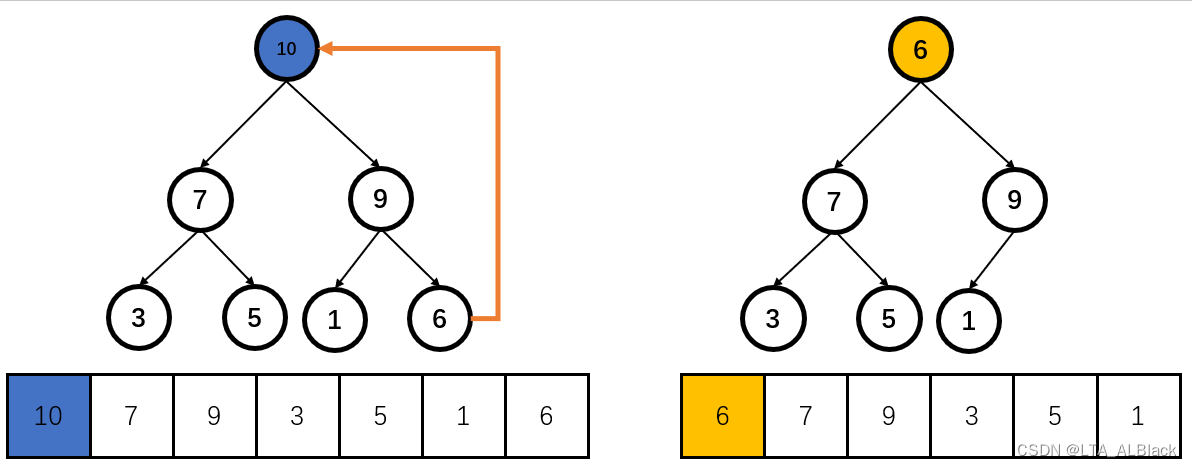
为何要删除是最后一个元素替换呢?很简单,因为对于顺序表来说,最后一个元素是能用\(O(1)\)删除的。替换之后,当前堆顶的元素一定都比他的儿子们要小了,因此令其向下探测调整。
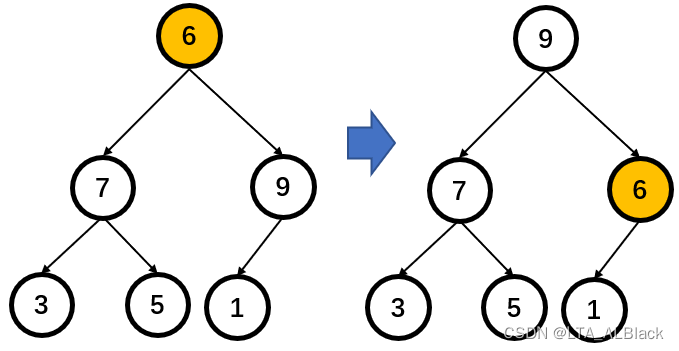
下侧的元素已经满足堆特性了,因为不要再考虑除根元素以外的其他结点的堆特性了。同样,弹出元素也只需要\(O(logN)\)的复杂度。删除的调整只有针对一个元素的一次向下探测,因此可以通过上述设计的adjustHeap函数的重用来实现。删除操作将是我们堆排序实现的核心思想!
三、堆排序的实现逻辑
我昨天在讲述简单选择排序的时候说过一句话,“ 简单排序最大的贡献其实还是其对于后续的堆排序提供的思路 ”。那么今天就来解释下这句话,简单排序本身是利用擂台思想,在无序序列中的元素通过一次大小比较选出极值元素,然后补充到有序序列中。这里“ 在无序序列中的元素通过一次大小比较选出极值元素 ”不正是我们堆能体现优势的地方吗?于是通过这种思想的启发,我们可以定义堆排序为:在无序序列中通过堆的调整与维护,确定出一个极值元素,然后将极值元素补充有序序列中。这正是我们堆排序的核心思想!
用图来描述下这个过程:
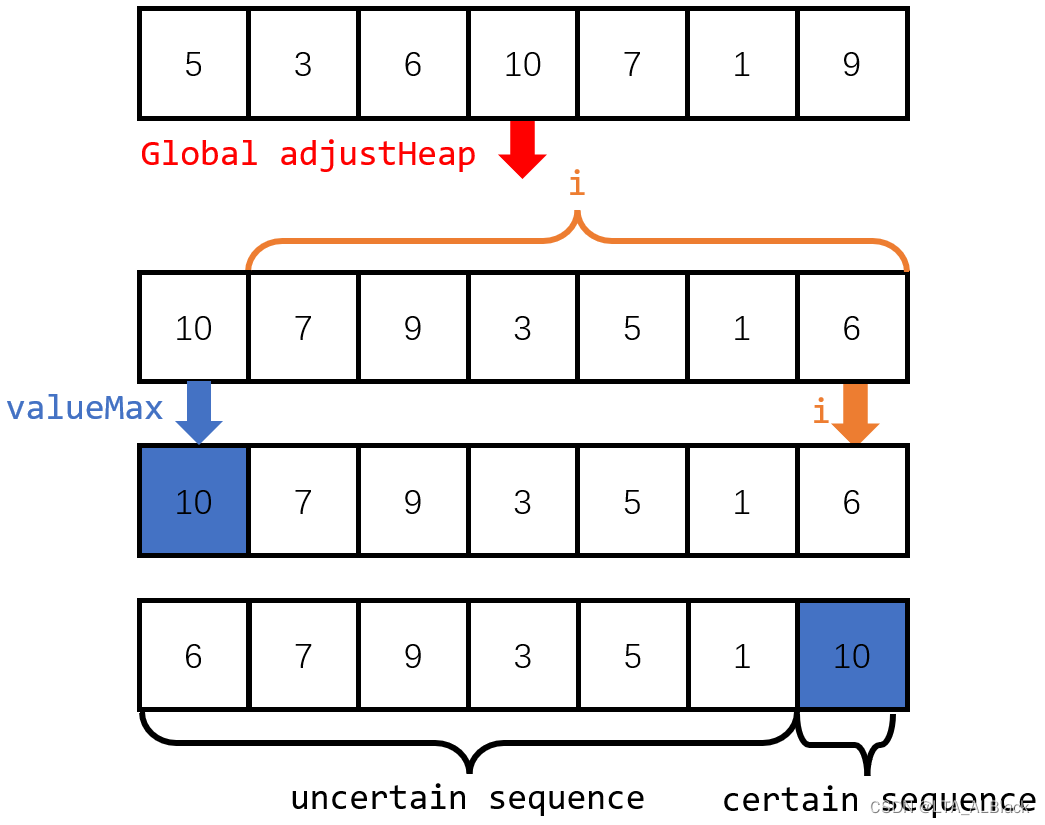
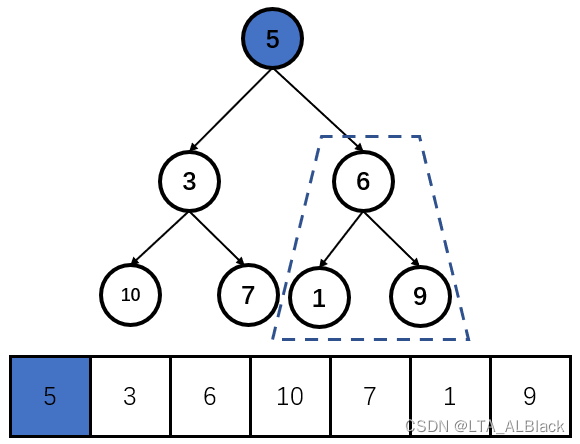
首先对于无序集合进行全局堆调整,得到一个堆结构。然后定义一个从后向前遍历的指针\(i\),这个指针\(i\)所指的位置,是希望有序序列在本回合能扩展到的范围下限。
因为当前得到的序列已经是一个大顶堆了,于是可以确定的是这时\(L[0]\)元素的值肯定是最大的,于是同结点\(i\)进行交换,交换后的区域\(L[i]\)成为有序序列的第一部分,之后都不再考虑这个数据区域。而范围\([0,i-1]\)内的原本堆特性已经被破环,于是需要再通过一次堆调整进行恢复:
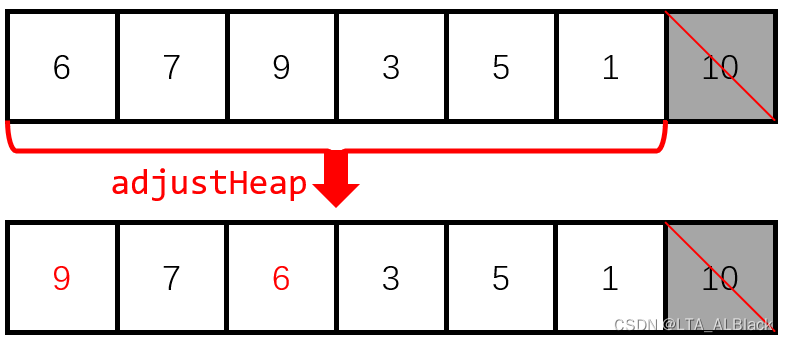
恢复完成之后,继续我们接下来的堆顶交换:
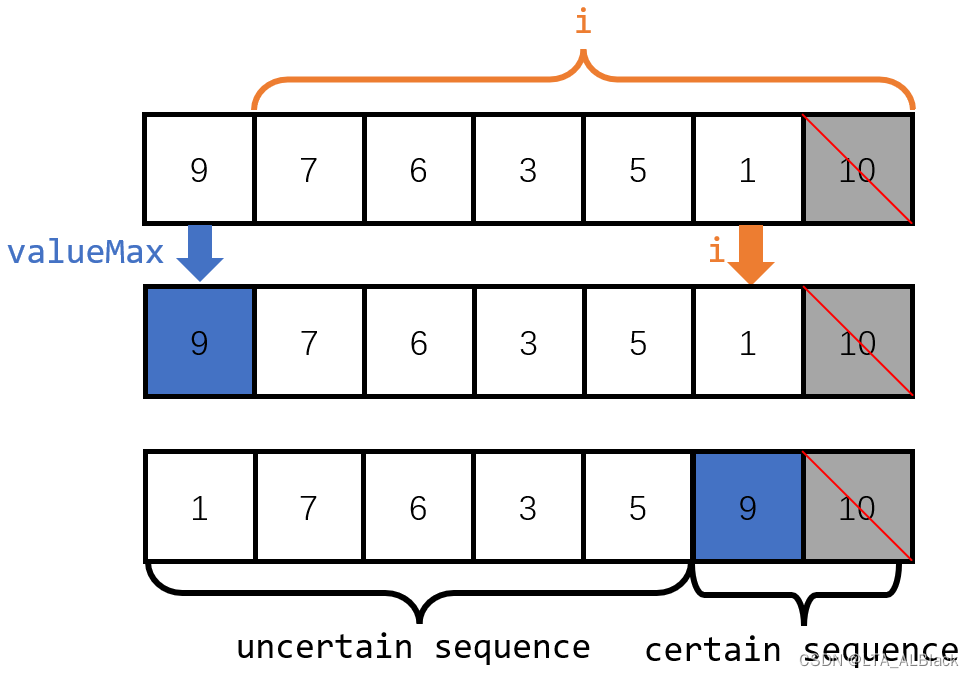
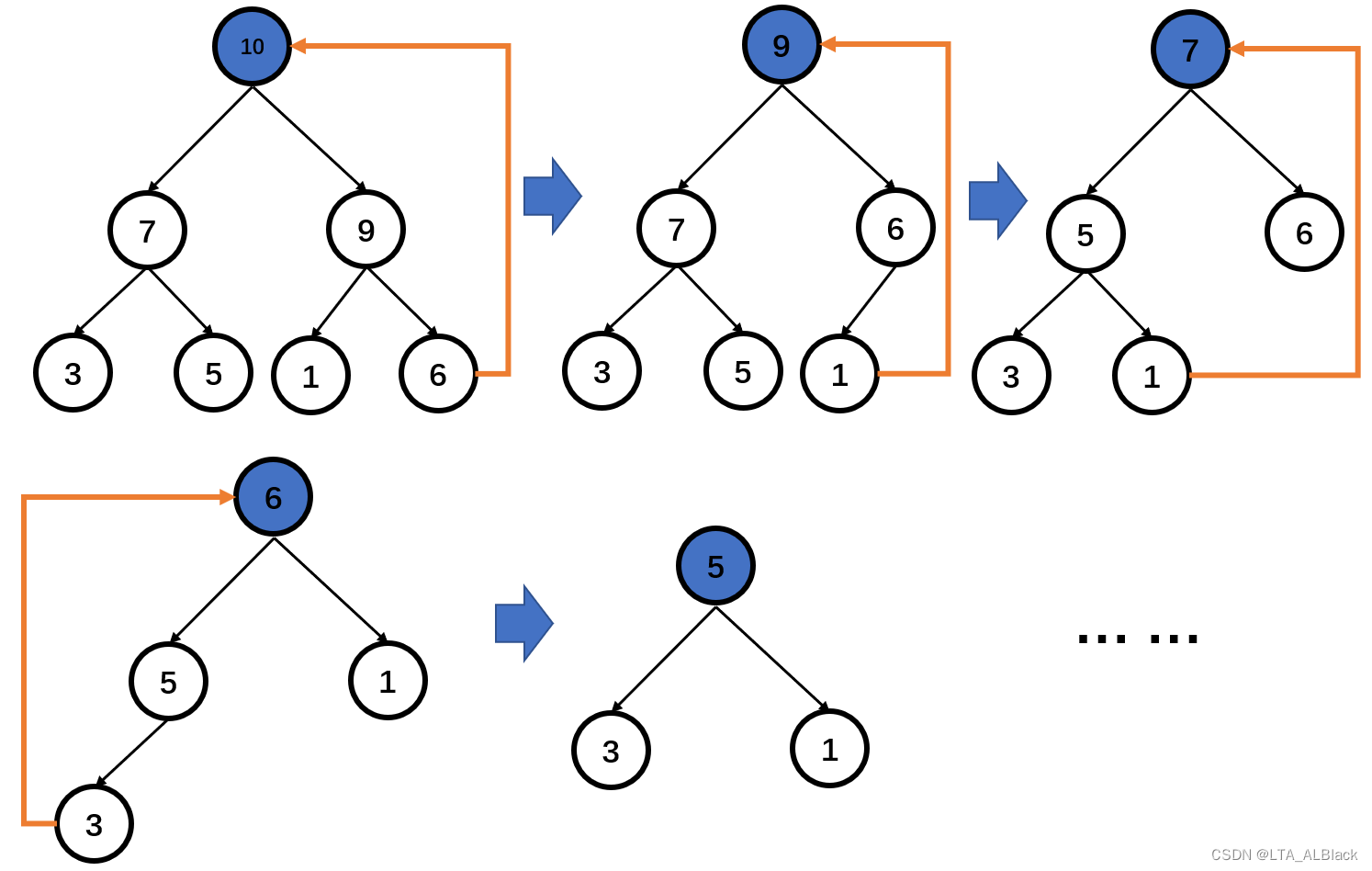
通过两轮维护,不知道是否体会到了这个过程的熟悉感?是的,这其实就是堆的删除(弹出),每次把堆顶元素交换到末尾,破环堆的特性,但是将最大的元素送了出来,构成有序序列的一部分。一方面,这运用到了类似于冒泡与简单选择排序的有序部分与无序部分分配治理,同时将无序部分一点点融入有序的实现;另一方面,这样也符合堆顶时刻是极值的特性,每次都取出堆顶的极值之间必然是有序的(例如下图对于堆逐步弹出的过程,其中蓝色结点都是即将弹出的堆顶元素,他们都是有序的)
因此后序的所有对维护只用像堆的删除操作后的维护那样只需要单次探测就好了,即\(O(logN)\)复杂度。
试想,我们是否可以把有序部分放在前面呢?其实是不行的。我们将有序部分放于后端是有所考量的,有序部分若在后端可以保证无序部分的范围一定是\([0,k] (0 ≤ k ≤ n-1)\)。这样可以保证每次交换后堆的结构仅有堆顶被破环和最后一个结点无伤大雅地删除,但是如果将堆的线性结构上限缩小,那么整个结构就彻底地与原本堆结构不一样了,届时可不是简单的一次向下探测就可以维护的了。
四、全部代码及其单元测试
/**
*********************
* Heap sort. Maybe the most difficult sorting algorithm.
*********************
*/
public void heapSort() {
DataNode tempNode;
// Step 1. Construct the initial heap.
for (int i = length / 2 - 1; i >= 0; i--) {
adjustHeap(i, length);
} // Of for i
System.out.println("The initial heap: " + this + "\r\n");
// Step 2. Swap and reconstruct.
for (int i = length - 1; i > 0; i--) {
tempNode = data[0];
data[0] = data[i];
data[i] = tempNode;
adjustHeap(0, i);
System.out.println("Round " + (length - i) + ": " + this);
} // Of for i
}// Of heapSort
/**
*********************
* Adjust the heap.
*
* @param paraStart The start of the index.
* @param paraLength The length of the adjusted sequence.
*********************
*/
public void adjustHeap(int paraStart, int paraLength) {
DataNode tempNode = data[paraStart];
int tempParent = paraStart;
int tempKey = data[paraStart].key;
for (int tempChild = paraStart * 2 + 1; tempChild < paraLength; tempChild = tempChild * 2 + 1) {
// The right child is bigger.
if (tempChild + 1 < paraLength) {
if (data[tempChild].key < data[tempChild + 1].key) {
tempChild++;
} // Of if
} // Of if
System.out.println("The parent position is " + tempParent + " and the child is " + tempChild);
if (tempKey < data[tempChild].key) {
// The child is bigger.
data[tempParent] = data[tempChild];
System.out.println("Move " + data[tempChild].key + " to position " + tempParent);
tempParent = tempChild;
} else {
break;
} // Of if
} // Of for tempChild
data[tempParent] = tempNode;
System.out.println("Adjust " + paraStart + " to " + paraLength + ": " + this);
}// Of adjustHeap
/**
*********************
* Test the method.
*********************
*/
public static void heapSortTest() {
int[] tempUnsortedKeys = { 5, 3, 6, 10, 7, 1, 9 };
String[] tempContents = { "if", "then", "else", "switch", "case", "for", "while" };
DataArray tempDataArray = new DataArray(tempUnsortedKeys, tempContents);
System.out.println(tempDataArray);
tempDataArray.heapSort();
System.out.println("Result\r\n" + tempDataArray);
}// Of heapSortTest因为在最初堆维护时也有打印操作,因此这里打印数据比较多:

性能与特性分析
我们在讲述堆排序的是并没有发生任何递归,全程是迭代完成,也没有创建任何辅助变量,因此堆排序是所有高级排序中空间消耗最小的。空间复杂度只有\(O(1)\)。同时,继承了简单交换排序的基础思想,堆排序在时间复杂度上也是固定地仅有\(O(NlogN)\),这使得其具有不受任何基本有无序数据干扰的特性。
堆排序是一个不稳定的排序,因为它每次都把堆顶元素同无序序列的最后一个元素交换,一旦这时堆中存在一个与堆顶元素一样的,但不位于堆最后的一个元素,那么这俩相同元素的相对位置就会发生变化。堆排序极度依靠顺序表的随机存储特性,因为这是将线性表抽象为树形结构的基础。因此堆排序只能兼容顺序表。
堆排序建立堆的过程需要对于无序数组全体进行维护,这是耗时最多的一次维护,对于每个分支结点要进行维护,复杂度可能在\(O(\frac{N}{2} logN)\)左右,但是每次维护的高度往往达不到\(logN\),因此,此复杂度很不准确。通过查阅网络有相关的复杂度证明,可以确定,建堆的维护时间复杂度大概稳定于\(O(N)\)。
(详情可见:建堆的时间复杂度分析_Black.Spider的博客-CSDN博客_建堆的时间复杂度)
排序中途停下观察,右侧的有序部分的位置即是排序结束后它的最终位置。这样的特性使得堆排序可以是“ 仅取数组前\(n\)大的元素 ”这种需求最优的算法,因为其实唯一一个可以在排序中途确定一些系列连续元素最终位置的复杂排序算法。为何如此说,快排虽然能确定最终位置,但是毕竟都是不连续的枢轴;归并只有在排序全部结束后才能确定。
总结
堆排这部分内容算是继我写快排之后最复杂的一篇,毕竟要讲清楚堆排序实现要先介绍堆这种结构,而这对于初学者来是说很陌生的一种结构,曾记得我当初最开始了解到堆的时候甚至还没学过树。
堆排序是所有本科基础排序算法中唯一一个使用到其他数据结构辅助完成的排序算法,而且这种特殊的结构还是专门为解决这个排序问题而顺带发明的一种特殊数据结构,可见,其相比于其他的排序算法来说,应该是更复杂和麻烦的。
此外,也需要注意到,Floyd与Williams为堆排序而量身打造的这种堆结构不仅在实现排序上展现了强大的威力,其中涉及的添加型维护与删除型维护是一种良好的,可用于优化许多算法最关键的操作,有时,这种结构本身对于算法领域的贡献可能远超了堆排序它本身!