目录
注意:这里是JAVA自学与了解的同步笔记与记录,如有问题欢迎指正说明
一、希尔排序的历史——伟大的突破者
希尔排序诞生于个世纪的50年代末期,正如我们在Dijkstra与Prim那部分提到的,50年代是计算机数据结构大量基础性算法蓬勃发展的时代,自然地,也诞生了众多基础的排序思想。但是随着算法一步步提出,人们逐渐发现排序的平均复杂度似乎永远无法突破\(O(N^2)\)大关。此时,计算机学术界充斥着“ 排序算法不可能突破\(O(N^2)\)的声音 ”。
这时,一位美国计算机科学家 Donald Shell敏锐察觉到了插入排序在基本有序的时候整体的复杂度是非常小的,于是基于这个特性,他通过添加了一个分割数组的增量序列,在分割的数组中进行插入排序。他于1959年发表了这种排序思想,这个神奇的思想一经提出就吸引了众多计算机研究者的注意,大家都相继找出各种优秀的增量序列来智证明这个算法的优越性。


但是值得可惜的是,直到如今,关于这种排序思想的复杂度证明仍然都是道难题,目前被大部分认可的Hibbard增量最糟糕的情况可以把复杂度稳定在\(O(N^{\frac{3}{2}})\)左右,而猜想的平均复杂度大概在\(O(N^{\frac{5}{4}})\),而Sedgewick增量序列的情况可能更好。但是这些猜想的平均复杂度都未被确切证明。但是值得肯定的是,这种缩小增量排序虽然最坏的情况下时间复杂度为\(O(N^2)\),但是通常情况下都要好于\(O(N^2)\)。
因此,这种缩小增量排序成为为第一个突破平方量级瓶颈的排序算法,打破了排序算法\(O(N^2)\)不可突破的神话,而此后进入60年代,各种诸如快排、堆排序等这种\(O(NlogN)\)量级的高级排序算法相继提出,使得排序思想进入了新的纪元。后来为了纪念这位伟大的突破者,以这第一位突破\(O(N^2)\)的科学家的名字命名了这个算法——shell排序算法(希尔排序算法)。
(以上部分内容来自互联网)
二、希尔排序的思想
正如上面所言,希尔排序就是通过增量序列将数组分割为特定区域,在每个区域内使用插入排序。举个例子,假如我们的增量序列是\(\{5,3,1\}\),以及待排序序列\(\{5, 3, 6, 10, 7, 1, 9, 12, 8, 4\}\)。我们不断使用增量去分割这个元素,首先是使用增量5分割为5个回合:
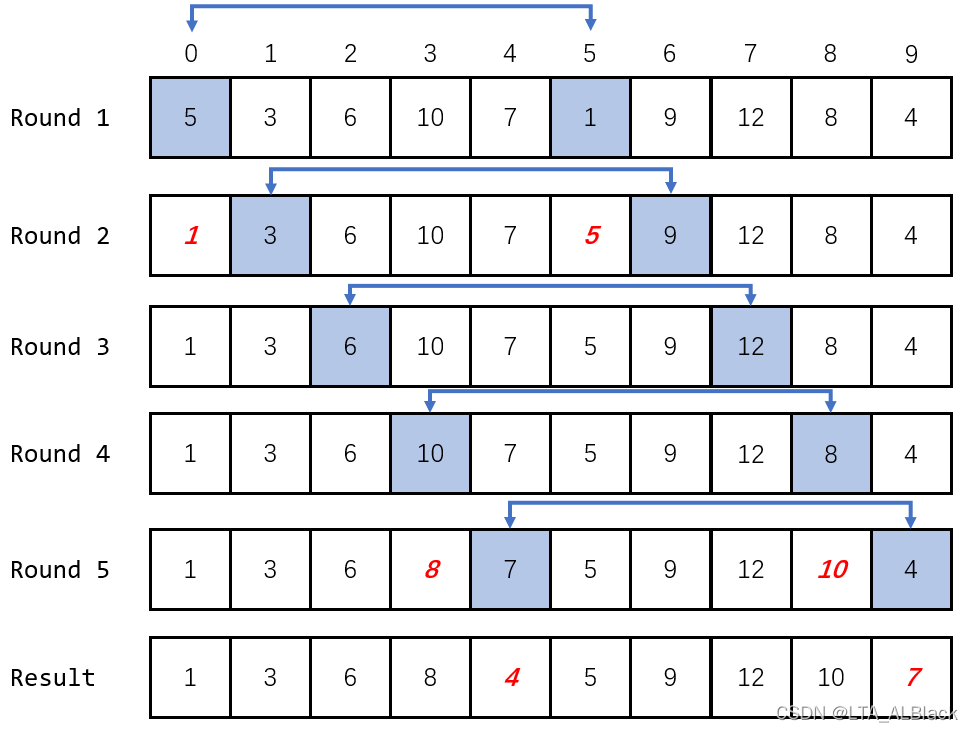
所谓增量\(d\),就是归纳当趟排序时,我们所关注的元素之间的间隔是\(d\),而这里增量\(d=5\)自然就是后一个元素下标是前一个元素下标+5得到的。若要包括全部元素,我们可以增加回合数目同时扩大初始开始下标而实现全覆盖。当划分完毕后,每回合的排序我都把目光只放到上图蓝色部分即可(增量序列覆盖范围),只对蓝色范围的内的数据使用直接插入排序(图上因为增量太大,所以每次都是针对两个元素的插入排序)。
为何要这么做?理由很简单。Donald Shell是基于插入排序在数组基本有序的优越性为特点提出的shell排序,这里间隔分隔可以尽可能均匀地有序分摊元素,保证了整体的有序,这样就不会出现特别大的元素在首部,特别小的元素在尾部的情况,这样在最后增量削减为\(d=1\)时(也就是进行正常的直接插入排序)其执行的复杂度就极其接近\(O(1)\)了。随着增量数目的增加,最终的直接插入排序的复杂度就越低,相对应的,前期增量调整的复杂度就会略有上升。这样就是为什么对于希尔排序来说选择恰当的增量非常关键。
我们后续把增量\(d=3\)与\(d=1\)的过程完善一下,见下图
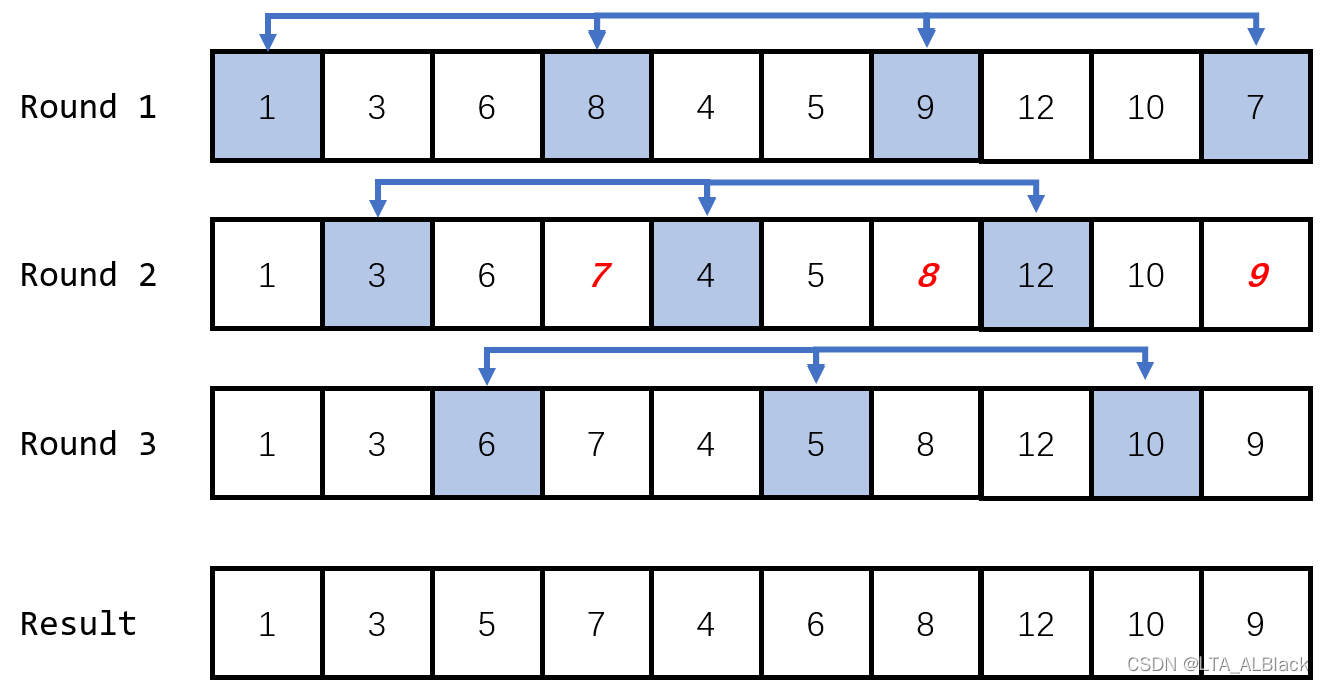
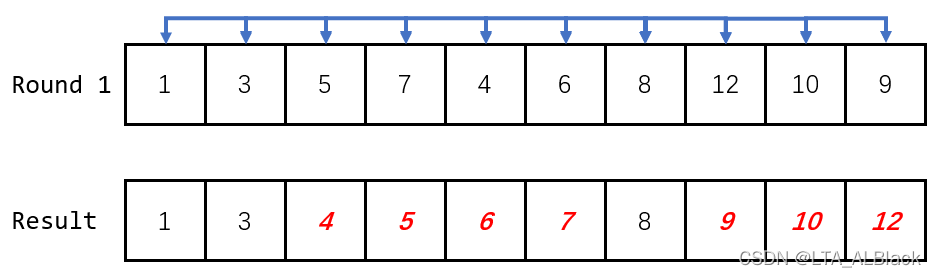
可以发现增量\(d=1\)时,我们挪动的元素都集中在一个范围内,的确不存在大范围的元素移动。同时我们发现了一个基本结论,当增量步长为\(d\)时,我们数组分割的回合数也刚好是\(d\),这个不难得出。因为第\(i\)回合的初始下标总是从\(i-1\)开始的,自然\(d+1\)回合的下标会从\(d\)开始。而这个的下标集合显然与第一回合的下标集合\(\{0,d,2d,...,nd\}(nd<length)\)相互重叠,因此分割的回合次数不得多于\(d\)次。
三、希尔排序的代码实现逻辑及其代码
这部分代码看懂实现内涵不容易,但是非重容易陷入看得懂写不来代码的窘境,这是由于这部分学习时大部分初学者都把大部分关注点投放到增量分割中了,所以搞懂了增量分割,但是还没懂得把插入排序的操作嵌套进来。所以下面我一边同步更新代码一边给大家说下代码实现逻辑过程。
首先由于本排序算法的特殊性,实现声明了一个tempJumpArray增量数组。然后接下来的第一个for循环就是轮流使用不同的增量元素来构造本轮的增量分割(并将其暂存于tempJump中,作为本轮分割的基本步长)
public void shellSort() {
DataNode tempNode;
int[] tempJumpArray = { 5, 3, 1 };
int tempJump;
int p;
for (int i = 0; i < tempJumpArray.length; i++) {
tempJump = tempJumpArray[i];
// Waiting for the supplement
// ...
} // Of for i
}// Of shellSort而后我们又添加了两个for循环:第一个for( j )循环是对于当前步长的循环,这个是由“ 确定当前增量后,增量分割的回合数等于增量\(d\)的值 "的规律决定的。
第二个for( k )循环,依次枚举了所有当前分割的全部元素,你可以将其理解为我们昨天讲的插入排序中对于全体数组元素的遍历。
public void shellSort() {
DataNode tempNode;
int[] tempJumpArray = { 5, 3, 1 };
int tempJump;
int p;
for (int i = 0; i < tempJumpArray.length; i++) {
tempJump = tempJumpArray[i];
for (int j = 0; j < tempJump; j++) {
for (int k = j + tempJump; k < length; k += tempJump) {
// Waiting for the supplement
// ...
} // Of for k
} // Of for j
System.out.println("Round " + i);
System.out.println(this);
} // Of for i
}// Of shellSort这个枚举效果如下图所示
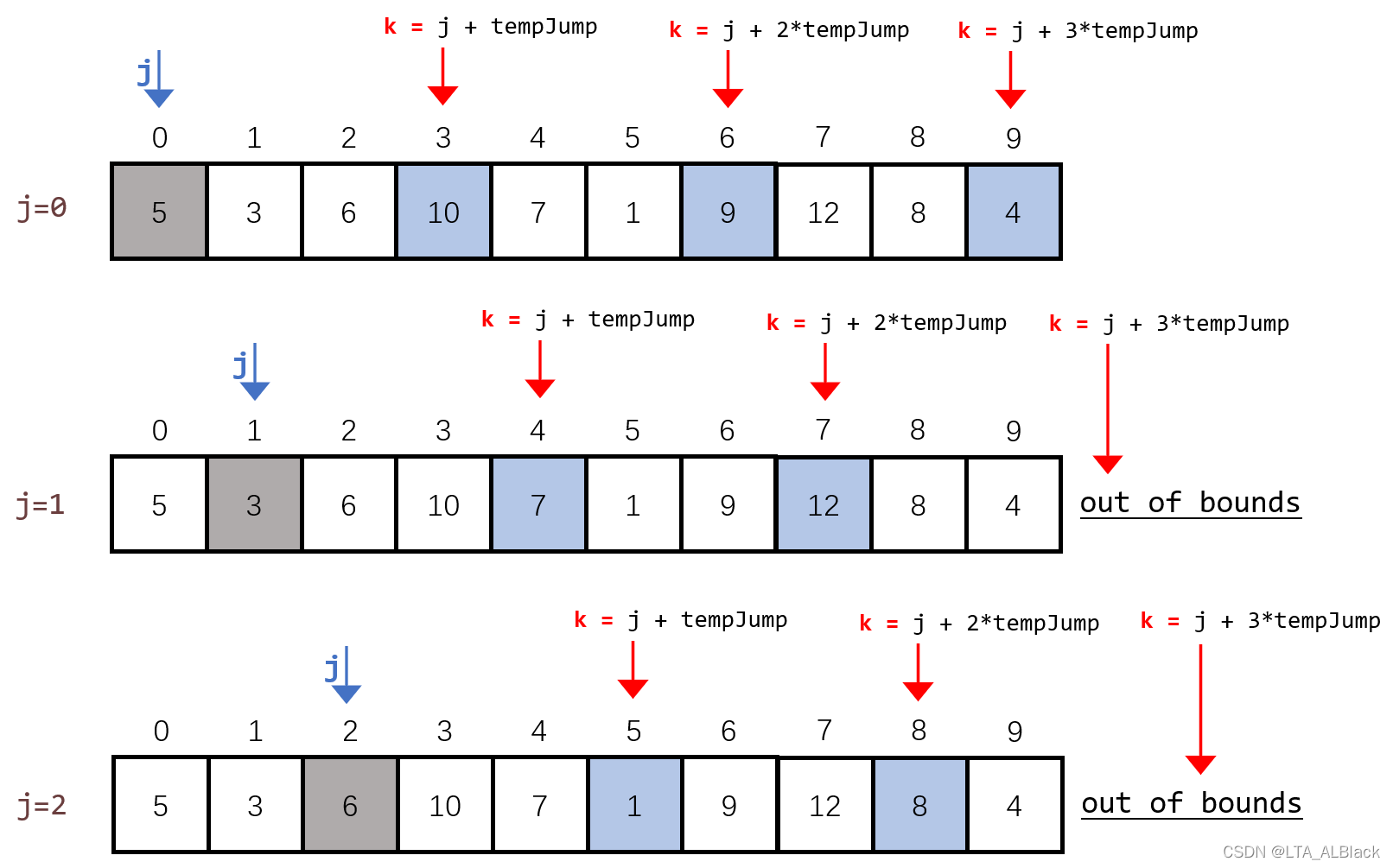
你可能会疑问,为什么我们要将k从当前增量分割数组的第二个元素开始,而不是第一个(灰色)。原因很简单,因为算法要求需对每个增量数组进行直接插入排序,而直接插入排序中的前半部分设置的是有序序列,而有序序列的最小情况就是一个元素,所以任何直接插入排序的第一个有效元素都是默认不作为预备元素的,且都从第二个元素开始循环。
然后接下来就是直接插入排序:
tempNode = data[k];
// Find the position to insert.
// At the same time, move other nodes.
for (p = k - tempJump; p >= 0; p -= tempJump) {
if (data[p].key > tempNode.key) {
data[p + tempJump] = data[p];
} else {
break;
} // Of if
} // Of for p
// Insert.
data[p + tempJump] = tempNode;我把昨天我们写的直接插入排序的核心代码部分放出来,让大家对比下。
tempNode = data[i];
// Find the position to insert.
// At the same time, move other nodes.
for (j = i - 1; data[j].key > tempNode.key; j--) {
data[j + 1] = data[j];
} // Of for j
// Insert.
data[j + 1] = tempNode;可见,因为方便理解,不过降低易读性,今天希尔排序内部的我们就没用哨兵思维了(希尔也不好用哨兵思维,因为增量数组的首元素是不确定的,不可能预留一个空的首元素)。所以今天代码的循环部分直接用" p >= 0 "来证明循环结束,在提前结束部分加入了break。
总代码与单元测试:
/**
*********************
* Shell sort. We do not use sentries here because too many of them are needed.
*********************
*/
public void shellSort() {
DataNode tempNode;
int[] tempJumpArray = { 5, 3, 1 };
int tempJump;
int p;
for (int i = 0; i < tempJumpArray.length; i++) {
tempJump = tempJumpArray[i];
for (int j = 0; j < tempJump; j++) {
for (int k = j + tempJump; k < length; k += tempJump) {
tempNode = data[k];
// Find the position to insert.
// At the same time, move other nodes.
for (p = k - tempJump; p >= 0; p -= tempJump) {
if (data[p].key > tempNode.key) {
data[p + tempJump] = data[p];
} else {
break;
} // Of if
} // Of for p
// Insert.
data[p + tempJump] = tempNode;
} // Of for k
} // Of for j
System.out.println("Round " + i);
System.out.println(this);
} // Of for i
}// Of shellSort
/**
*********************
* Test the method.
*********************
*/
public static void shellSortTest() {
int[] tempUnsortedKeys = { 5, 3, 6, 10, 7, 1, 9, 12, 8, 4 };
String[] tempContents = { "if", "then", "else", "switch", "case", "for", "while", "throw", "until", "do" };
DataArray tempDataArray = new DataArray(tempUnsortedKeys, tempContents);
System.out.println(tempDataArray);
tempDataArray.shellSort();
System.out.println("Result\r\n" + tempDataArray);
}// Of shellSortTest
这个测试样例与我们上述的图内数据是一致的,不妨对比(结果一致)
性能与特性分析
希尔排序的空间复杂度为\(O(1)\),最差的复杂度为\(O(N)\),但是最好的复杂度与平均复杂度的说法不一,在第一部分我们也说过了,Hibbard增量最糟糕的情况可以把复杂度稳定在\(O(N^{\frac{3}{2}})\)左右,而猜想的平均复杂度大概在\(O(N^{\frac{5}{4}})\),而Sedgewick增量序列可以让最坏复杂度稳定在为\(O(N^{\frac{4}{3}})\),平均复杂度在\(O(N^{\frac{7}{6}})\),但是这些说法都没有完善的证明,这部分的证明至今仍然是个难题,有兴趣的读者可以去看看。总之可以记住,希尔排序的平均复杂度在合理的增量序列下是要明显优于\(O(N^2)\)的。 甚至可以断言,希尔排序大多数情况下效率都高于简单排序,甚至在合适的增量和N的情况下, 还好于快速排序。(现实有存在这样的案例,有兴趣的小伙伴可以试试PTA的这道题:6-11 求自定类型元素序列的中位数,让你体验希尔屠杀快排的“乐趣” Σ( ° △ °|||))
希尔排序是一个不稳定的算法,这个不稳定要归咎增量序列分割了相同值元素之间的关系,相同值的元素可能不会被划入同个增量序列中,而当前增量序列重排后,这相同值元素之间的相对关系很可能被破坏了。
希尔排序只能是用于顺序表,因为排序过程中使用了不断变化的步长增加,这个过程若要分配指针完成任务量太大而且不确定。同时在排序中途停下来,任取一个之前移动的过的元素,我们都无法确定当前位置是否是这个元素排序完毕后的最终位置。
总结
希尔排序确实是一种非常奇怪的排序,在学习排序的时候我们常常见到两大类的内部排序,再除开例如桶排序和基数排序这种走捷径的排序。大体上排序就可分为简单排序与高级排序两大类,简单排序则是以插入、冒泡、简单选择为代表,而高级排序就诸如快排、堆排、归并这类。
这时,希尔排序的地位就显得尴尬了,他是唯一地一个基于简单排序思维而实现部分高级排序的效率的“ 怪胎 ”,你可以理解是,他是这两大排序的中间体,是一种过渡性质的算法。而恰好历史上这个算法提出的时间也确实挤在了这两大算法的分水岭中,是第一个突破\(O(N^2)\)的排序算法,这是它的第一怪。他的平均复杂度的证明格外困难,至今仍是许多研究者在研究的问题,这是它的第二怪。总的来看,希尔排序就像是盘旋在排序算法上空一个古怪的云朵,奇妙而惊奇,述说着排序思想神奇的魅力。