图形学笔记(一)图形学概览:图形学的定义、应用、学习内容、参考读物、与视觉的区别
图形学笔记(三)变换——缩放、镜像、切变
此节对应虎书第二章(Miscellaneous Math)与第五章(Linear Algebra)
1. 图形学所需基础
1.1 基础数学
- 线性代数,微积分,统计 Linear algebra,calculus,statics
1.2 基础物理
- 光学,力学 Opitics,Mechanics
1.3 其他
- 信号处理 Signal processing (走样、反走样)
- 数值分析 Numerical analysis
需要一点美学…
2. 向量Vectors
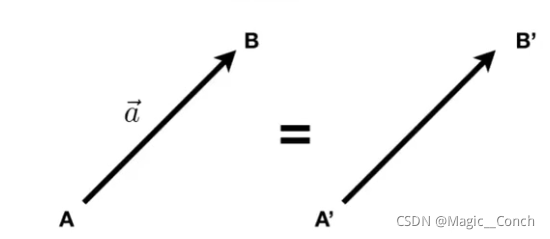
2.1 向量的基本性质
- 写作 a ⃗ \vec a a 或粗体的 a
- 由起点和终点表示 A B → \overrightarrow{AB} AB
- 具有方向和长度
- 没有绝对的开始位置
2.2 向量标准化
- 向量的长度写作 || a ⃗ \vec a a||
2.2.1 单位向量
- 单位向量是长度为1的向量
- 单位向量的获得: a ^ \hat a a^= a ⃗ \vec a a/|| a → \overrightarrow a a||
- 使用单位向量来代表方向
2.3 向量的基本操作
2.1 向量相加
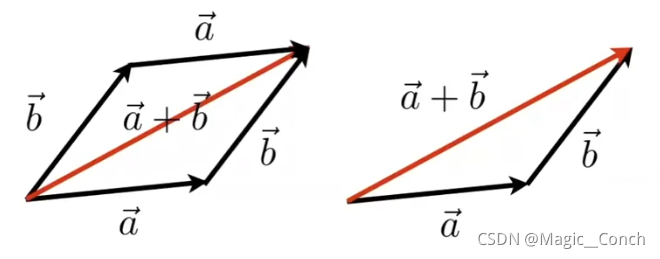
- 几何上:平行四边形法则(左)和三角形法则(右)。
- 代数上:简单的坐标相加
2.2 向量的表示

- 笛卡尔坐标系中的X和Y可以是任何向量(通常是垂直的)
- 一般向量表示是列向量
A = ( x y ) A= \begin{pmatrix} x \\ y \\ \end{pmatrix} A=(xy)
也可以转置来表示成行向量:
A T = ( x , y ) A^T=(x,y) AT=(x,y)
计算向量长度:
∥ A ∥ = x 2 + y 2 \Vert A \Vert=\sqrt {x^2+y^2} ∥A∥=x2+y2
2.3 向量的点乘

2.3.1 点乘的基本运算
a → ⋅ b → = ∥ a → ∥ ∥ b → ∥ cos θ \overrightarrow a · \overrightarrow b = \Vert \overrightarrow a \Vert \Vert \overrightarrow b \Vert \cos\theta a⋅b=∥a∥∥b∥cosθ
- 点乘可以获得夹角:
cos θ = a → ⋅ b → ∥ a → ∥ ⋅ ∥ b → ∥ \cos\theta = \cfrac{\overrightarrow a · \overrightarrow b }{\Vert\overrightarrow a\Vert ·\Vert \overrightarrow b\Vert} cosθ=∥a∥⋅∥b∥a⋅b - 对于单位向量:
cos θ = a ^ ⋅ b ^ \cos\theta = \hat a · \hat b cosθ=a^⋅b^
注意:向量点乘最后得到的是一个数。
2.3.2 点乘的性质
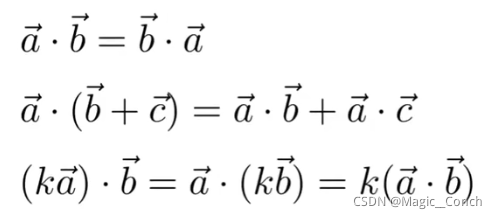

2.3.3 在笛卡尔坐标系下的点乘运算:
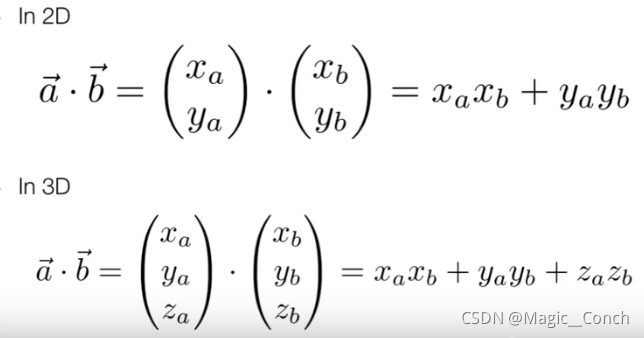
2.3.4 点乘在图形学的应用
- 找到两个向量的夹角:光来的方向、物体表面的法线、相机看的方向等等的夹角可以通过这个运算得到。
- 找到一个向量投影到一个向量的结果
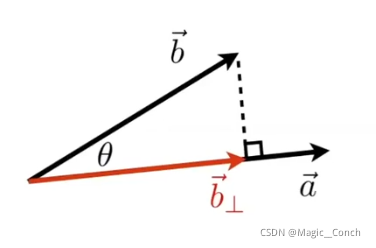
其中, b → ⊥ \overrightarrow b_\bot b⊥是 b → \overrightarrow b b在 a → \overrightarrow a a上的投影,且 b → ⊥ \overrightarrow b_\bot b⊥ 是沿着 a → \overrightarrow a a或者 a ^ \hat a a^的。有以下公式,其中k是向量长度:
b → ⊥ = k a ^ \overrightarrow b_\bot = k \hat a b⊥=ka^
k = ∥ b → ⊥ ∥ = k a ^ = ∥ b → ∥ cos θ k = \Vert \overrightarrow b_\bot \Vert = k \hat a =\Vert \overrightarrow b \Vert\cos\theta k=∥b⊥∥=ka^=∥b∥cosθ
2.3.5 投影的用处:
- 投影可以让一个向量分解成两个向量。(这两个向量互相垂直)
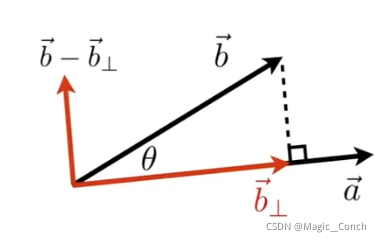
如图所示,计算出投影后,垂直于向量 b ⃗ \vec b b投影方向的分量可以通过 b ⃗ − b ⃗ ⊥ \vec b - \vec b_\bot b−b⊥获得。 - 根据点乘的结果计算两个方向有多么接近
- 判断前与后的信息
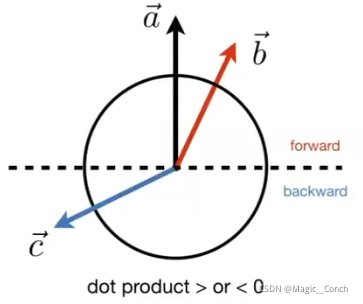
如图所示,虚心将圆分割成两半,如果在forward区域内(点乘>0),就说 a ⃗ \vec a a与 b ⃗ \vec b b是同向的,点乘为1说明完全同向,在backward区域内(点乘>0),就说 a ⃗ \vec a a与 b ⃗ \vec b b是反向的,点乘为-1说明完全相反。点乘为0说明垂直。
2.4 向量的叉乘
2.4.1 基本概念

- 叉积是两个向量的垂直向量,即叉积得到的向量与另外两个向量都垂直。
- 方向通过右手(螺旋)定则判断。能看出来向量的叉积不满足交换律,交换后的结果是相反的。
eg:判断从 a ⃗ \vec a a到 b ⃗ \vec b b就让四指的方向从 a ⃗ \vec a a到 b ⃗ \vec b b,大拇指的方向就是叉积的方向。 - 对构建坐标系是有用的。如果三轴满足 x ⃗ × y ⃗ = z ⃗ \vec x \times \vec y = \vec z x×y=z,则这个坐标系是右手坐标系。,但是一些软件是左手坐标系,需要注意。
2.4.2 叉积的性质

2.4.3 笛卡尔坐标系下的叉乘
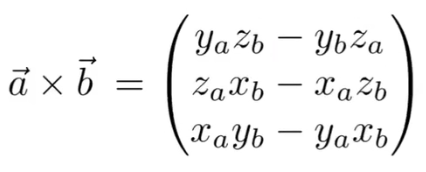
叉乘也可以表示为矩阵形式:
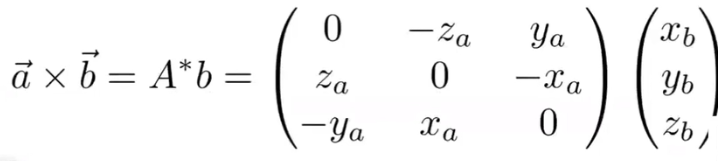
2.4.3 叉乘在图形学中的作用
- 判断左和右

如果 a ⃗ \vec a a顺时针旋转能到 b ⃗ \vec b b,就说 a ⃗ \vec a a在 b ⃗ \vec b b的左侧,逆时针就是右侧。
计算 a ⃗ \vec a a与 b ⃗ \vec b b的叉积,如果叉积的z是正的,就说明 b ⃗ \vec b b在 a ⃗ \vec a a的左侧,叉积的z是负的,就是在右侧。
例如上图中, b ⃗ \vec b b在 a ⃗ \vec a a的左侧, - 判断内与外
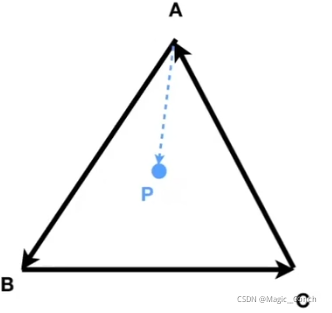
如图所示, A B ⃗ × A P ⃗ > 0 \vec {AB} \times \vec {AP} > 0 AB×AP>0,说明P在AB的左边, B C ⃗ × B P ⃗ > 0 \vec {BC} \times \vec {BP} > 0 BC×BP>0,说明P在BC的左边 , C A ⃗ × C P ⃗ > 0 \vec {CA} \times \vec {CP} > 0 CA×CP>0 ,说明P在CA的左边。
如果进行三个叉积运算的结果都为正或都为负,表明点都在三角形边的左边或者都在右边,故说明P在三角形内部。
否则说明点在三角形外面。
- 直角坐标系的确定与坐标

3.矩阵
3.1 什么是矩阵
- 矩阵是数字的排列。( m × n m \times n m×n的矩阵是m行,n列的。)

- 矩阵的加法和数乘就是对矩阵的每一个元素都相加或都乘以这个数。
3.2 矩阵的乘积
3.2.1 可以做乘积的条件
第一个矩阵的列数必须等于第二个矩阵的行数,M行N列和N行P列做叉积,结果是M行P列的。

3.2.2 乘积的运算
结果矩阵中(i,j)位置的数是A中第i行和B中第j列的点积。
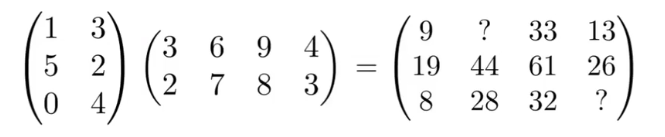
eg:在上图中,26(结果矩阵2行4列)=5(左边2行)·4(右边4列)+2(左边2行)·3(右边4列)
3.2.3 矩阵乘积的性质
- 没有交换律
- 满足结合律(括号随便放,左右不能换)和分配律
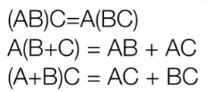
- 与向量做乘积时,把向量当作列向量(m × \times × 1)
- 矩阵的乘积对变化很重要
eg:求镜像
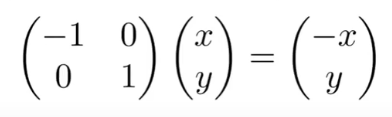
3.3 矩阵的转置
- 矩阵的转置:交换矩阵的行和列(ij->ji)

- 转置的性质:
( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT
3.4 特殊矩阵
3.4.1 单位矩阵
只有主对角线的元素不为0,且全都为1的矩阵,记为I。
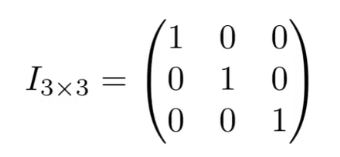
3.4.2 矩阵的逆
- 逆矩阵的定义:与该矩阵相乘能得到单位矩阵的矩阵称为逆矩阵(两矩阵互逆)。

- 逆矩阵的性质
( A B ) − 1 = B − 1 A − 1 (AB)^{-1} = B^{-1}A^{-1} (AB)−1=B−1A−1
4. 向量点乘和叉乘的矩阵形式
4.1 点乘的矩阵形式
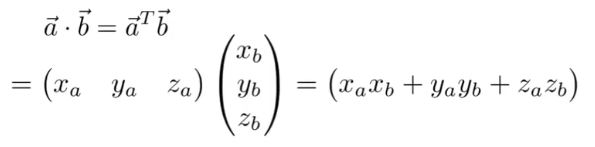
4.2 叉乘的矩阵形式

其中 A ∗ A^* A∗是伴随矩阵。