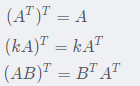矩阵基础
1. 什么是矩阵
线性代数中把矩阵定义为:由m×n 个元素按m 行,n 列的方式排列,就得到矩阵,用下面的方式表示

通常用一个加粗的大写字母表示一个矩阵,例如矩阵A可以用 A 来表示
2. 矩阵的运算
2.1 矩阵加法
只有相同维度的矩阵才可以进行加法运算,即m×n的矩阵与m×n的矩阵才能相加,得到的结果还是一个m×n的矩阵,每个元素等于相加矩阵对应位置元素的和
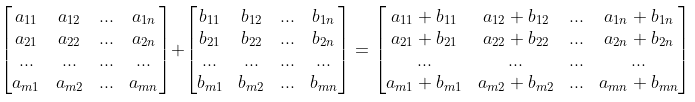
矩阵加法适用的运算定律
交换律 A + B = B + A
结合律 (A + B) + C = A + (B + C)
示例
A = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
B = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
A + B = [
1.0+1.0, 2.0+2.0, 3.0+3.0,
4.0+4.0, 5.0+5.0, 6.0+6.0,
7.0+7.0, 8.0+8.0, 9.0+9.0,
]
2.2 矩阵减法
与矩阵加法类似,也只有相同维度的矩阵才可以进行减法运算,即m×n的矩阵与m×n的矩阵才能相减,得到的结果还是一个m×n的矩阵,每个元素等于被减数矩阵对应位置元素与减数矩阵对应位置元素的差
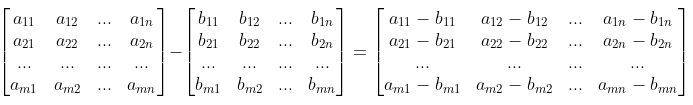
示例
A = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
B = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
A - B = [
1.0-1.0, 2.0-2.0, 3.0-3.0,
4.0-4.0, 5.0-5.0, 6.0-6.0,
7.0-7.0, 8.0-8.0, 9.0-9.0,
]
2.3 矩阵数乘
数乘是矩阵与一个常数相乘,一个m×n的矩阵与一个常数k相乘,得到的结果还是一个m×n的矩阵,每个元素等于矩阵对应位置元素与这个常数的乘积
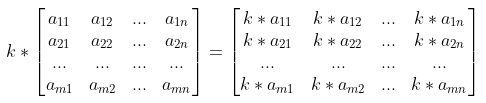
矩阵数乘适用的运算定律
分配律 (k + v)A = kA + vA
分配律 k(A + B) = kA + kB
结合律 (kv)A = k(vA)
示例
A = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
k = 3.0
k * A = [
3.0*1.0, 3.0*2.0, 3.0*3.0,
3.0*4.0, 3.0*5.0, 3.0*6.0,
3.0*7.0, 3.0*8.0, 3.0*9.0,
]
2.4 矩阵的转置
矩阵转置是指将一个矩阵的行列互换的操作,一个m×n的矩阵转置后,得到的结果是一个n×m的矩阵,最终得到一个与原矩阵行列位置互换的矩阵,例如原矩阵中第三行第二列的元素是a32,转置后变为新矩阵第二行第三列的元素
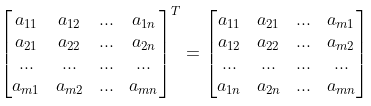
矩阵转置适用的运算定律
注:A与B相乘的结果再转置不等于A的转置乘以B的转置,而是等于B的转置乘以A的转置,注意先后顺序
A = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
k = 3.0
A(转置) = [
1.0, 4.0, 7.0,
2.0, 5.0, 8.0,
3.0, 6.0, 9.0
]
2.5 矩阵的乘法
矩阵的乘法相对其他运算比较复杂,两个矩阵可以相乘必须满足一个条件被乘矩阵的列数等于乘数矩阵的行数,例如:(m×n)(n×p) = (m×p),就是说m行n列的矩阵与n行p列的矩阵相乘结果为一个m行p列的矩阵,可以相乘的前提条件是前一个矩阵的列数与后一个矩阵的行数相等
接下来看看矩阵相乘是如何运算的,以一个3×3的矩阵为例说明


A = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
B = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
AB = [
1.0*1.0+2.0*4.0+3.0*7.0, 1.0*2.0+2.0*5.0+3.0*8.0, 1.0*3.0+2.0*6.0+3.0*9.0,
4.0*1.0+5.0*4.0+6.0*7.0, 4.0*2.0+5.0*5.0+6.0*8.0, 4.0*3.0+5.0*6.0+6.0*9.0,
7.0*1.0+8.0*4.0+9.0*7.0, 7.0*2.0+8.0*5.0+9.0*8.0, 7.0*3.0+8.0*6.0+9.0*9.0,
]
矩阵相乘适用的运算定律
分配律 A(B + C) = AC + BC
分配律 (A + B)C = AC + BC
结合律 (AB)C = A(BC)
注:矩阵A乘以矩阵B,不等于B乘以矩阵A
2.6 矩阵与向量相乘
任何一个向量可以用一维矩阵表示,可以表示为列向量,也可以表示为一个行向量,都表示同一个向量
列向量 a
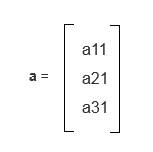
a 向量转置后变成行向量

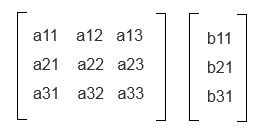
两个矩阵可以相乘必须满足一个条件被乘矩阵的列数等于乘数矩阵的行数
所以当向量与矩阵相乘是需要转换成以下两种形式
矩阵右乘列向量
矩阵左乘行向量
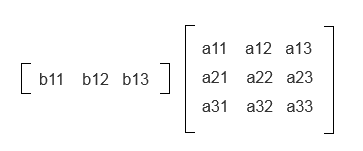
计算过程参照向量相乘的运算过程,只是要更少的计算过程
示例
A = [
1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0
]
B = [
1.0,
2.0,
3.0,
]
AB = [
1.0*1.0+2.0*2.0+3.0*3.0,
4.0*1.0+5.0*2.0+6.0*3.0,
7.0*1.0+8.0*2.0+9.0*3.0,
]
2.7 使用矩阵表示向量点积
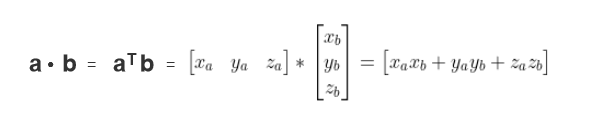
2.8 使用矩阵表示向量叉积
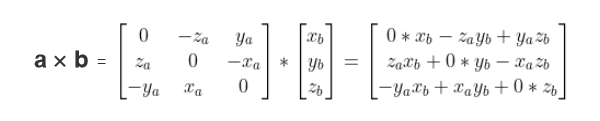
3 一些特殊的矩阵
3.1 单位矩阵
一个矩阵的对角线上(从左上角到右下角的对角线)的元素均为1,其余的元素都是0的矩阵称为单位矩阵
二维单位矩阵表示为
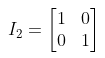
三维单位矩阵表示为
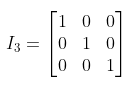
3.1 逆矩阵
若有矩阵 A 和矩阵 B,且 AB = BA = Ⅰ, Ⅰ为单位矩阵,则矩阵A和矩阵B互逆,称矩阵A可逆,矩阵B是矩阵A的逆矩阵
逆矩阵的一些性质
一个矩阵乘以自身逆矩阵等于单位向量,则它的逆矩阵乘以自己也等于单位向量
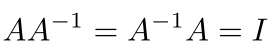
一个矩阵的逆矩阵再作逆运算结果是自己本身
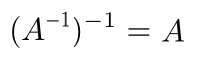
两个矩阵相乘再作逆运算等于后一个矩阵的逆矩阵乘以前一个矩阵的逆矩阵
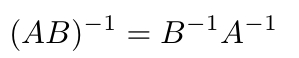
3.1 对角矩阵
一个矩阵的对角线上(从左上角到右下角的对角线)的元素外其余的元素都是0的矩阵称为对角矩阵,对角矩阵主要用于缩放变换
3.1 正交矩阵
若果有矩阵A,满足条件矩阵A乘以矩阵A的转置矩阵是一个单位矩阵,即满足下面的公式
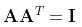
则矩阵A被称为正交矩阵
正交阵的一些性质
正交矩阵的转置等于它的逆矩阵
正交矩阵的每一行都是单位向量,且俩俩正交
正交矩阵的每每一列都是单位向量,且俩俩正交