三维空间刚体运动4-4:四元数线性插值方法:Spring-1
序:本篇系列文章参照高翔老师《视觉SLAM十四讲从理论到实践》,讲解三维空间刚体运动。博文将原第三讲分为四部分来讲解,其中四元数部分较多较复杂,又分为四部分,总体目录如下:
- 旋转矩阵和变换矩阵;
- 旋转向量表示旋转;
- 欧拉角表示旋转;
- 四元数包括以下部分:
4-1. 四元数表示变换;
4-2. 四元数线性插值方法:LinEuler/LinMat/Lerp/Nlerp/Slerp;
4-3. 四元数多点插值方法:Squad;
4-4. 四元数多点二次插值方法:Spring。
1. 总述:多点旋转插值的数学方法
之前提到的插值方法是相对较简单的基于旋转表示的方法。原则上,插值方法应独立于该方法的旋转方式。另外,对于最优插值算法的定义应体现出旋转空间期望的属性。当然,最优曲线也可以在算法上显式的写为旋转表达式。
比如以下两个旋转间的插值:最优插值曲线等同于旋转空间的一条直线,这条最优插值曲线在算法上可以写作欧拉角的表达方式,但是使用四元数形式的Slerp。Slerp的优势是表述更简洁(可参考之前《三维空间刚体运动4-1:四元数表示变换》第1章和第4章所述的旋转空间和单位四元数球体的等价性)。
因此,我们将基于旋转空间讨论插值问题,我们将给出最优插值曲线的基本数学要求,这是为了给出最优插值曲线算法描述,并据此寻找符合条件的插值算法。
2. 插值曲线及其连续性
2.1 插值曲线定义
旋转间的插值定义在特殊正交群 S O ( 3 ) SO(3) SO(3)的旋转空间中,关于特殊正交群 S O ( 3 ) SO(3) SO(3)请参考《三维空间刚体运动1:旋转矩阵与变换矩阵》第2章的内容。然而,如之前所述, S O ( 3 ) SO(3) SO(3)与 H 1 H_{1} H1是拓扑等价的,因此我们选择在单位四元数空间中定义通用的插值方法:
定义:对于给定的 k k k个控制点 q i ∈ H 1 q_{i} \in H_{1} qi∈H1,并且 I = [ t 1 , . . . , t k ] I=[t_{1},...,t_{k}] I=[t1,...,tk],插值曲线 γ ( t ) : I ∝ H 1 \gamma(t):I\propto H_{1} γ(t):I∝H1,即对于 t i ∈ I t_{i}\in I ti∈I,有 γ ( t i ) ≡ q i \gamma(t_{i})\equiv q_{i} γ(ti)≡qi,同时要求 t 1 ≤ t 2 , . . . , t k − 1 ≤ t k t_{1}\leq t_{2},...,t_{k-1} \leq t_{k} t1≤t2,...,tk−1≤tk。
2.2 插值曲线连续性的讨论
通常希望插值曲线是“漂亮”的,这个较模糊的字眼通常意味着曲线在微分几何层面是平滑的。但是,由于存在多个不同的平滑定义故需求并不明确,定义列举如下:
使 γ ( t ) \gamma(t) γ(t)是某曲线在 C n ( I , R n ) C^{n}(I,R^{n}) Cn(I,Rn)上的参数表达式,平滑性可被定义为下列方式:
(1)[Madsen, 1991]:如果 γ ( t ) ∈ C 1 \gamma(t)\in C^{1} γ(t)∈C1,并且 ∀ t ∈ I : γ ′ ( t ) ≠ 0 \forall t\in I:\gamma ^{'}(t)\neq 0 ∀t∈I:γ′(t)=0,那么曲线 γ ( t ) \gamma(t) γ(t)是平滑的。
(2)[Schwarz, 1989]:如果 γ ( t ) ∈ C 2 \gamma(t)\in C^{2} γ(t)∈C2,那么曲线 γ ( t ) \gamma(t) γ(t)是平滑的。
(3)[Jakobsen, 1993]:如果 γ ( t ) ∈ C ∞ \gamma(t)\in C^{\infty} γ(t)∈C∞,那么曲线 γ ( t ) \gamma(t) γ(t)是平滑的。
以上不同定义对于“漂亮”的表述并不明朗,我们还需要进一步检查到底需要插值曲线的哪些性质,如下图所示:
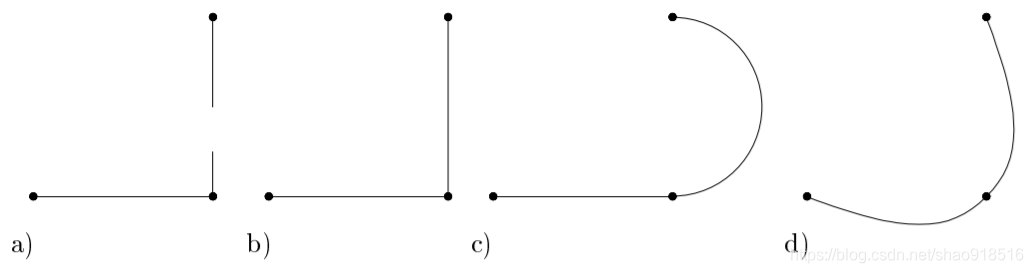
上图表示平面中三个控制点间的插值曲线,其中:a)非连续插值曲线;b)连续插值曲线;c) C 1 C^{1} C1连续插值曲线;d) C 2 C^{2} C2连续插值曲线。
很明显,我们希望曲线必须是连续且可微的,不希望在动态曲线上出现洞或断点,因此我们要求插值曲线至少必须是 C 1 C^{1} C1。至于是否需要 C 2 C^{2} C2甚至 C ∞ C^{\infty} C∞还不确定。
由于控制点是对称的(双倍覆盖),因此也希望插值曲线是对称的。平面上展示的曲线明确表示我们至少需要 C 2 C^{2} C2而不是 C 1 C^{1} C1,然而平面展示的曲线并不是采用 C 2 C^{2} C2的充分条件,因此目前采用几阶连续并不明朗,因此,我们将这一决定推迟到下一篇Spring中。
在 γ ( t ) \gamma(t) γ(t)平滑性的第一条定义中要求 γ ′ ( t ) ≠ 0 \gamma^{'}(t)\neq 0 γ′(t)=0,这意味着插值函数不能包含奇点。现在看来,这是一个合理的要求。然而,某些情况也有可能对插值曲线的速度提出合理但矛盾的要求。例如,考虑一个钟摆的动画,控制点(它们定义钟摆摆动的角度)将位于旋转空间的直线上。在外部位置(即端点处),钟摆应该没有速度,这与插值函数中的奇点相对应。因此,我们也将这一决定推迟到下一篇Spring中。
关于平滑性的讨论并没有给我们带来太多的启发。上面的定义甚至无法让我们区分LinEuler、Lerp和Slerp,这些曲线都是 C 2 C^{2} C2(但在控制点处是 C 0 C^{0} C0)。因此,仅仅描述插值曲线应该属于哪一类函数是不够的。
3. 最优插值曲线
3.1 最优插值曲线的引出
对平滑性的考量对插值曲线的定义没有给出充分的需求,我们需要一个客观明确的指标来衡量我们的曲线在旋转空间中的“漂亮”程度。
我们将再次在平面中寻找灵感(见下图)。如前所述,三次曲线通常用于在一系列点之间的插值。三次曲线有很多种,在上一篇4.3中描述的贝塞尔曲线就是一个例子,而最常见的一类曲线是样条曲线。

上图表示平面中的样条插值:a)简单线性插值;b)样条插值曲线。
讨论样条曲线,我们必须像其他严谨的项目处理样条曲线那样,写一点关于造船者的故事。传统上,当造船者想要决定如何塑造一艘船的弯曲部分时,会使用一块有弹性的金属,这块金属被固定在一组铆钉之间。然后,金属部件与铆钉相适应,形成一个优美柔和的曲线。造船者称这个工具为样条。关于样条的知识也请参考上一篇4.3中描述的样条。
从物理上看,上面对样条的描述对应于金属片在铆钉约束条件下,达到最小的内部张力。从数学角度讲,金属件使曲率(curvature)最小。曲率是指一条(平面上的)曲线在特定一点弯曲的程度,它正比于曲线转过的角度,反比于曲线的长度。关于曲率的知识请参考《什么是曲率和曲率半径》。
在平面中,这个曲线可以描述如下:给定控制点 ( x i , y i ) ∈ R 2 (x_{i},y_{i})\in \mathbb{R}^{2} (xi,yi)∈R2,定义曲线 γ ( t ) ∈ C 2 ( I , R 2 ) \gamma(t)\in C^{2}(I,\mathbb{R}^{2}) γ(t)∈C2(I,R2),其中 t t t是自然参数(如曲线长度,0-1之间的进度比等),并且使 γ ( t ) \gamma(t) γ(t)经过控制点,同时最小化表达式 ∫ I ∥ γ ′ ′ ( t ) ∥ 2 d t \int _{I}\left \| \gamma ^{''}(t) \right \| ^{2}dt ∫I∥∥∥γ′′(t)∥∥∥2dt,此时曲率的平方最小。
这个简单的公式从微分几何中的一般概念出发,给出了插值曲线的明确定义。因此,我们选择将曲率(或曲率平方)最小的曲线视为最优插值曲线。下面我们将看到,在 H 1 H_{1} H1中计算这条曲线并不像在平面上那么简单。
3.2 最优插值曲线在 H 1 H_{1} H1的曲率
插值曲线位于四元数空间的超球面 H 1 H_{1} H1上,假设 t t t为自然参数,那么曲线 γ ( t ) \gamma (t) γ(t)的曲率通常被定义为 ∥ γ ′ ′ ( t ) ∥ \left \| \gamma ^{''}(t) \right \| ∥∥∥γ′′(t)∥∥∥。
这里解释一下,上文关于曲率的资料中,二阶可导函数的曲率被定义为: K ( t ) = ∥ γ ′ ′ ( t ) ∥ ( 1 + γ ′ ( t ) 2 ) 3 2 (3.1) K(t)=\frac{\left \| \gamma ^{''}(t) \right \|}{(1+\gamma ^{'}(t)^{2})\frac{3}{2}}\tag{3.1} K(t)=(1+γ′(t)2)23∥∥∥γ′′(t)∥∥∥(3.1)然而在本篇论文中,曲率的分母被省略,论文并没给出解释,博主认为,这里的曲率 ∥ γ ′ ′ ( t ) ∥ \left \| \gamma ^{''}(t) \right \| ∥∥∥γ′′(t)∥∥∥是曲线在切平面上的投影的曲率,并非原曲线,而切平面在投影后已固定,分母可以作为常数处理,因此省略掉分母。另外一种原因,固定 γ ′ ( t ) \gamma ^{'}(t) γ′(t)可能有助于最小化角加速度,未定,后续补充。
插值曲线Slerp在四元数单位圆上产生大弧线(大弧线概念请参考本系列博文4-2的5.2.2节), H 1 H_{1} H1上的圆弧在切平面上的投影是一条直线,因此,可以预料大弧线的投影是没有曲率的。如果用 ∥ γ ′ ′ ( t ) ∥ \left \| \gamma ^{''}(t) \right \| ∥∥∥γ′′(t)∥∥∥来计算曲率,曲率将不是零,而是1:即单位球的曲率。因此,我们想计算相对于四元数单位球面的曲率,而不是相对于四元数空间。我们称这个曲率为局部曲率。
曲面上曲线的局部曲率的定义是基于微分几何的。点的局部曲率定义如下:给定表面上的点,一个坐标系统(地图)被放置在切平面。现在曲线的局部曲率就是投影到切平面上的曲线的曲率。这也叫做正切曲率。
在微分几何中,大弧线(直线)称为测地线。测地线投影到切面上,就成了一条直线。因此,正如预期的那样,我们看到大弧线没有任何局部弯曲。下面开始分析正切曲率。
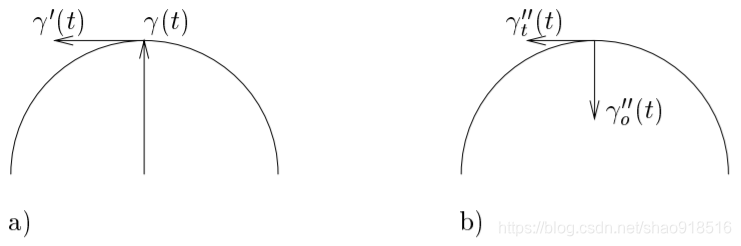
上图表示曲线 γ ( t ) \gamma (t) γ(t)的正切向量 γ ′ ( t ) \gamma ^{'}(t) γ′(t)和正切曲率 γ ′ ′ ( t ) \gamma ^{''}(t) γ′′(t)在平面的分量:a)表示位于四元数单位球面上曲线的位置向量 γ ( t ) \gamma (t) γ(t)(位置矢量是在某一时刻,以坐标原点为起点,以运动质点所在位置为终点的有向线段),它在正切平面上的投影为 γ ′ ( t ) \gamma ^{'}(t) γ′(t);b)向量 γ ′ ′ ( t ) \gamma ^{''}(t) γ′′(t)可以分解为正切平面的分量 γ t ′ ′ ( t ) \gamma ^{''}_{t}(t) γt′′(t)和平行于位置矢量的分量 γ o ′ ′ ( t ) \gamma ^{''}_{o}(t) γo′′(t)。
由上图可知,如果曲线 γ ( t ) \gamma (t) γ(t)位于 H 1 H_{1} H1的表面,我们可以将 γ ′ ′ ( t ) \gamma ^{''}(t) γ′′(t)分解为两个部分 γ t ′ ′ ( t ) \gamma ^{''}_{t}(t) γt′′(t)、 γ o ′ ′ ( t ) \gamma ^{''}_{o}(t) γo′′(t)。期望的曲率部分是 γ t ′ ′ ( t ) \gamma ^{''}_{t}(t) γt′′(t),因为它表示 γ ′ ′ ( t ) \gamma ^{''}(t) γ′′(t)的弯曲程度。因此,曲线 γ ( t ) \gamma (t) γ(t)的局部曲率 κ \kappa κ可以表示为: κ ( r , t ) = ∥ γ t ′ ′ ( t ) ∥ = ∥ γ ′ ′ ( t ) − γ o ′ ′ ( t ) ∥ \kappa (r,t)=\left \| \gamma ^{''}_{t}(t) \right \|=\left \| \gamma ^{''}(t)-\gamma ^{''}_{o}(t) \right \| κ(r,t)=∥∥∥γt′′(t)∥∥∥=∥∥∥γ′′(t)−γo′′(t)∥∥∥
由于曲线 γ ( t ) \gamma (t) γ(t)位于 H 1 H_{1} H1的表面, γ o ′ ′ ( t ) \gamma ^{''}_{o}(t) γo′′(t)平行于 γ ( t ) \gamma (t) γ(t),因此 γ o ′ ′ ( t ) \gamma ^{''}_{o}(t) γo′′(t)可以表示为 γ ′ ′ ( t ) \gamma ^{''}(t) γ′′(t)投影到 γ ( t ) \gamma (t) γ(t),参考《三维空间刚体运动2:旋转向量与罗德里格斯公式》中的投影公式(2.6),因此: γ t ′ ′ ( t ) = γ ′ ′ ( t ) − γ o ′ ′ ( t ) = γ ′ ′ ( t ) − ( γ ′ ′ ( t ) ⋅ γ ( t ) ∥ γ ( t ) ∥ ) γ ( t ) ∥ γ ( t ) ∥ = γ ′ ′ ( t ) − ( γ ′ ′ ( t ) ⋅ γ ( t ) ) γ ( t ) \begin{aligned} \gamma ^{''}_{t}(t) &= \gamma ^{''}(t)-\gamma ^{''}_{o}(t) \\&= \gamma ^{''}(t)-\left ( \gamma ^{''}(t) \cdot \frac{\gamma (t)}{\left \| \gamma (t) \right \|} \right )\frac{\gamma (t)}{\left \| \gamma (t) \right \|} \\&= \gamma ^{''}(t) - (\gamma ^{''}(t) \cdot \gamma (t))\gamma (t) \end{aligned} γt′′(t)=γ′′(t)−γo′′(t)=γ′′(t)−(γ′′(t)⋅∥γ(t)∥γ(t))∥γ(t)∥γ(t)=γ′′(t)−(γ′′(t)⋅γ(t))γ(t)由此给出局部曲率 κ \kappa κ的定义:给定 γ ( t ) ∈ C 2 ( I , H 1 ) \gamma(t)\in C^{2}(I,H_{1}) γ(t)∈C2(I,H1),局部曲率 κ ( γ , t ) \kappa(\gamma, t) κ(γ,t)被定义为: κ ( γ , t ) = ∥ γ ′ ′ ( t ) − ( γ ′ ′ ( t ) ⋅ γ ( t ) ) γ ( t ) ∥ (3.2) \kappa(\gamma, t)=\left \| \gamma ^{''}(t) - (\gamma ^{''}(t) \cdot \gamma (t))\gamma (t) \right \|\tag{3.2} κ(γ,t)=∥∥∥γ′′(t)−(γ′′(t)⋅γ(t))γ(t)∥∥∥(3.2)注意,这里 t t t不一定是自然参数。因此,上述定义在严格的微分几何意义上是不正确的。在自然参数上参数化的曲线的曲率可写作 κ ( r , t ) = ∥ γ ′ ′ ( t ) ∥ \kappa (r,t)=\left \| \gamma ^{''}(t) \right \| κ(r,t)=∥∥∥γ′′(t)∥∥∥,而对于光滑曲线,微分几何上的正确表达式为: κ ( γ , t ) = ∥ γ ′ ′ ( t ) ∥ γ ′ ( t ) ∥ 2 − γ ′ ( t ) ( γ ′ ′ ( t ) ⋅ γ ′ ( t ) ) ∥ γ ′ ( t ) ∥ 4 ∥ \kappa(\gamma, t)=\left \| \frac{\gamma ^{''}(t)}{\left \| \gamma^{'}(t) \right \|^{2}} - \frac{\gamma^{'}(t) (\gamma ^{''}(t) \cdot \gamma^{'}(t))}{\left \| \gamma^{'}(t) \right \|^{4}}\right \| κ(γ,t)=∥∥∥∥∥∥γ′(t)∥2γ′′(t)−∥γ′(t)∥4γ′(t)(γ′′(t)⋅γ′(t))∥∥∥∥∥然而,我们感兴趣的不仅仅是插值曲线的形状(曲率)。我们还想要一个“漂亮的”角速度函数,即使角加速度最小化的函数(从物理角度来看,对应的是使能量最小化)。在表达式3.2中角加速度是自动包括在内的,因为我们没有重新参数化自然参数。因此我们使用表达式3.2来计算曲率。
下面将分别介绍正切曲率 κ ( γ , t ) \kappa(\gamma, t) κ(γ,t)在 H 1 H_{1} H1上的连续解析解(第4章)、连续半解析解(第5章)和离散数字化解(篇幅原因,留至下篇)。
4. 正切曲率 κ ( γ , t ) \kappa(\gamma, t) κ(γ,t)在 H 1 H_{1} H1上的连续解析解
4.1 函数 K ( γ ) K(\gamma) K(γ)及变分法
我们将H1中的最优插值曲线定义为曲率平方和最小的曲线,但又必须通过控制点的限制,然后定义了H1中曲率的相关表达式。因此,我们得到问题的公式如下:
设控制点 q 1 , . . . , q N ∈ H 1 q_{1},...,q_{N}\in H_{1} q1,...,qN∈H1,求 γ ( t ) ∈ C 2 ( I , H 1 ) \gamma(t)\in C^{2}(I,H_{1}) γ(t)∈C2(I,H1),使存在 t 1 , . . . , t N ∈ ( I ) t_{1},...,t_{N}\in (I) t1,...,tN∈(I),满足 γ ( t i ) = q i \gamma(t_{i})=q_{i} γ(ti)=qi,并使下列表达式最小化: K ( γ ) = ∫ t 1 t N ∥ κ ( γ , t ) ∥ 2 d t (4.1) K(\gamma)=\int_{t_{1}}^{t_{N}}\left \| \kappa (\gamma,t) \right \|^{2}dt\tag{4.1} K(γ)=∫t1tN∥κ(γ,t)∥2dt(4.1)这里将求以 γ \gamma γ为变量的曲率问题 κ ( γ , t ) \kappa (\gamma,t) κ(γ,t)转换为对曲率平方的积分问题 K ( γ ) K(\gamma) K(γ),同样以函数 γ \gamma γ为变量。这里 K ( γ ) K(\gamma) K(γ)求的是整条曲线各个点的曲率平方之和,当它越小时,转弯就越平滑,所耗费的动能也就越少,符合导航线路的基本要求。
使函数的积分最小化的问题叫做变分演算问题,又称变分法。关于变分法请参考文章《变分法入门介绍》,这里不再赘述。在这里应用变分法只要记住,求极值应用到的必要条件是一阶导数为零。
下面,我们将概述变分学中解决问题的基本方法。 K ( γ ) K(\gamma) K(γ)达到最小值的一个必要条件是 K ′ ( γ ) = 0 K^{'}(\gamma)=0 K′(γ)=0,对于 δ ∈ R \delta \in \mathbb{R} δ∈R和 ψ ∈ C k ( I , H 1 ) \psi \in C^{k}(I,H_{1}) ψ∈Ck(I,H1),我们看一下导数定义: lim δ → 0 K ( γ + δ ψ ) − K ( γ ) δ = 0 (4.2) \lim_{\delta\rightarrow 0}\frac{K(\gamma+\delta \psi)-K(\gamma)}{\delta}=0\tag{4.2} δ→0limδK(γ+δψ)−K(γ)=0(4.2)上式中,函数 δ ψ \delta \psi δψ称为 γ \gamma γ的变量函数,函数 γ + δ ψ \gamma+\delta \psi γ+δψ称为比较函数。满足边界条件的函数 γ ( t ) ∈ C 2 ( I , H 1 ) \gamma(t)\in C^{2}(I,H_{1}) γ(t)∈C2(I,H1)称为容许函数。这样,我们就得到了关于 γ \gamma γ的条件函数。
4.2 求解 γ \gamma γ
现在我们将推导出变分问题的解必须满足的要求。因此,我们假定解 γ \gamma γ和比较函数 γ + δ ψ \gamma+\delta \psi γ+δψ都是可容许的,并且 K ( γ ) K(\gamma) K(γ)是最小的。
比较函数 γ + δ ψ \gamma+\delta \psi γ+δψ若要被容许,前提必须是: ψ ( t 1 ) = ψ ( t 2 ) = . . . = ψ ( t N ) = 0 (4.3) \psi (t_{1}) = \psi (t_{2}) = ... = \psi (t_{N}) = 0\tag{4.3} ψ(t1)=ψ(t2)=...=ψ(tN)=0(4.3)此外,由于 γ \gamma γ和 γ + δ ψ \gamma+\delta \psi γ+δψ在单位球面上,我们有 ∥ γ ∥ = 1 \left \| \gamma \right \|=1 ∥γ∥=1和 ∥ γ + δ ψ ∥ = 1 \left \| \gamma+\delta \psi\right \|=1 ∥γ+δψ∥=1。在下面的推导中,可以忽略表达式成分中包含四元数函数这一情况。这是因为没有使用四元数乘法(只使用标量乘积)。
因此,交换性没有问题。因此我们有: 1 = ∥ γ + δ ψ ∥ 2 = ∥ γ ∥ 2 + δ 2 ∥ ψ ∥ + 2 δ ( γ ⋅ ψ ) = 1 + δ ( δ ∥ ψ ∥ + 2 γ ⋅ ψ ) ⇒ γ ⋅ ψ = − δ 2 ∥ ψ ∥ 2 (4.4) \begin{aligned} 1 &= \left \| \gamma + \delta \psi \right \|^{2} \\&= \left \| \gamma \right \|^{2} + \delta^{2}\left \| \psi \right \| + 2\delta(\gamma \cdot \psi) \\&= 1 + \delta(\delta\left \| \psi \right \| + 2\gamma \cdot \psi) \\ \Rightarrow \gamma \cdot \psi &= -\frac{\delta}{2}\left \| \psi \right \|^{2}\end{aligned}\tag{4.4} 1⇒γ⋅ψ=∥γ+δψ∥2=∥γ∥2+δ2∥ψ∥+2δ(γ⋅ψ)=1+δ(δ∥ψ∥+2γ⋅ψ)=−2δ∥ψ∥2(4.4)我们想用关于"导数"的知识来检验 K ( γ + δ ψ ) − K ( γ ) K(\gamma+\delta \psi)-K(\gamma) K(γ+δψ)−K(γ): K ( γ + δ ψ ) − K ( γ ) = ∫ t 1 t N ∥ κ ( γ + δ ψ , t ) ∥ 2 − ∥ κ ( γ , t ) ∥ d t = ∫ t 1 t N ∥ ( γ + δ ψ ) ′ ′ − ( ( γ + δ ψ ) ′ ′ ⋅ ( γ + δ ψ ) ) ( γ + δ ψ ) ∥ 2 − ∥ γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ∥ 2 d t = ∫ t 1 t N ∥ γ ′ ′ + δ ψ ′ ′ − ( γ ′ ′ ⋅ γ + δ γ ′ ′ ⋅ ψ + δ γ ψ ′ ′ + δ 2 ψ ′ ′ ⋅ ψ ) ( γ + δ ψ ) ∥ 2 − ∥ γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ∥ 2 d t = ∫ t 1 t N ∥ [ γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ] + δ [ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ψ − ( γ ′ ′ ⋅ ψ ) γ − ( ψ ′ ′ ⋅ γ ) γ ) ] + δ 2 [ . . . ] + δ 3 [ . . . ] ∥ 2 − ∥ γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ∥ 2 d t \begin{aligned} K(\gamma+\delta \psi)-K(\gamma) &= \int_{t_{1}}^{t_{N}}\left \| \kappa (\gamma+\delta\psi,t) \right\|^{2} - \left \| \kappa (\gamma,t) \right \|dt \\&= \int_{t_{1}}^{t_{N}}\left \| (\gamma+\delta\psi)^{''}-((\gamma+\delta\psi)^{''}\cdot(\gamma+\delta\psi))(\gamma+\delta\psi) \right \|^{2} - \left \| \gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma \right \|^{2}dt \\&= \int_{t_{1}}^{t_{N}}\left \| \gamma^{''} + \delta\psi^{''}-(\gamma^{''}\cdot\gamma+\delta\gamma^{''}\cdot\psi+\delta\gamma\psi^{''}+\delta^{2}\psi^{''}\cdot\psi)(\gamma+\delta\psi) \right \|^{2} - \left \| \gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma \right \|^{2}dt \\&= \int_{t_{1}}^{t_{N}}\left \| [\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma] + \delta[\psi^{''}-(\gamma^{''}\cdot\gamma)\psi-(\gamma^{''}\cdot\psi)\gamma-(\psi^{''}\cdot\gamma)\gamma)] + \delta^{2}[...] + \delta^{3}[...]\right \|^{2} \\ &\quad\quad- \left \| \gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma \right \|^{2}dt\end{aligned} K(γ+δψ)−K(γ)=∫t1tN∥κ(γ+δψ,t)∥2−∥κ(γ,t)∥dt=∫t1tN∥∥∥(γ+δψ)′′−((γ+δψ)′′⋅(γ+δψ))(γ+δψ)∥∥∥2−∥∥∥γ′′−(γ′′⋅γ)γ∥∥∥2dt=∫t1tN∥∥∥γ′′+δψ′′−(γ′′⋅γ+δγ′′⋅ψ+δγψ′′+δ2ψ′′⋅ψ)(γ+δψ)∥∥∥2−∥∥∥γ′′−(γ′′⋅γ)γ∥∥∥2dt=∫t1tN∥∥∥[γ′′−(γ′′⋅γ)γ]+δ[ψ′′−(γ′′⋅γ)ψ−(γ′′⋅ψ)γ−(ψ′′⋅γ)γ)]+δ2[...]+δ3[...]∥∥∥2−∥∥∥γ′′−(γ′′⋅γ)γ∥∥∥2dt在上述表达式中,我们根据 δ \delta δ的指数收集了多项式。上述推导的目的是求导数。 K ( γ + δ ψ ) − K ( γ ) K(\gamma+\delta \psi)-K(\gamma) K(γ+δψ)−K(γ)的展开式中,被 δ 2 \delta^{2} δ2和 δ 3 \delta^{3} δ3乘的多项式可以被删除,因为在检查极限时,除以 δ \delta δ后,当 δ \delta δ无限接近零时它们就消失了。因此,上面表达式可被写为: K ( γ + δ ψ ) − K ( γ ) = ∫ t 1 t N ∥ A + δ B ∥ 2 − ∥ A ∥ 2 d t = ∫ t 1 t N δ 2 ∥ B ∥ 2 + 2 δ A ⋅ B d t \begin{aligned} K(\gamma+\delta \psi)-K(\gamma) &= \int_{t_{1}}^{t_{N}}\left \| A+\delta B \right \|^{2} - \left \| A \right \|^{2}dt \\&= \int_{t_{1}}^{t_{N}}\delta^{2}\left \| B \right \|^{2}+2\delta A\cdot Bdt\end{aligned} K(γ+δψ)−K(γ)=∫t1tN∥A+δB∥2−∥A∥2dt=∫t1tNδ2∥B∥2+2δA⋅Bdt这里 A = γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ , B = ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ψ − ( γ ′ ′ ⋅ ψ ) γ − ( ψ ′ ′ ⋅ γ ) γ ) A=\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma,B=\psi^{''}-(\gamma^{''}\cdot\gamma)\psi-(\gamma^{''}\cdot\psi)\gamma-(\psi^{''}\cdot\gamma)\gamma) A=γ′′−(γ′′⋅γ)γ,B=ψ′′−(γ′′⋅γ)ψ−(γ′′⋅ψ)γ−(ψ′′⋅γ)γ)。同样省略被 δ 2 \delta^{2} δ2乘的项,重写表达式为: K ( γ + δ ψ ) − K ( γ ) = ∫ t 1 t N 2 δ [ γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ] [ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ψ − ( γ ′ ′ ⋅ ψ ) γ − ( ψ ′ ′ ⋅ γ ) γ ) ] d t = 2 δ ∫ t 1 t N γ ′ ′ ⋅ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) − ( γ ′ ′ ⋅ ψ ) ( γ ′ ′ ⋅ γ ) − ( γ ⋅ ψ ′ ′ ) ( γ ′ ′ ⋅ γ ) − ( γ ′ ′ ⋅ γ ) ( γ ⋅ ψ ′ ′ ) + ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ γ ) ( γ ⋅ ψ ) + ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) ( γ ⋅ γ ) + ( γ ′ ′ ⋅ γ ) ( γ ⋅ ψ ′ ′ ) ( γ ⋅ γ ) d t \begin{aligned} K(\gamma+\delta \psi)-K(\gamma) &= \int_{t_{1}}^{t_{N}}2\delta[\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma][\psi^{''}-(\gamma^{''}\cdot\gamma)\psi-(\gamma^{''}\cdot\psi)\gamma-(\psi^{''}\cdot\gamma)\gamma)]dt \\&= 2\delta\int_{t_{1}}^{t_{N}}\gamma^{''}\cdot\psi^{''}-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)-(\gamma^{''}\cdot\psi)(\gamma^{''}\cdot\gamma)-(\gamma\cdot\psi^{''})(\gamma^{''}\cdot\gamma)-(\gamma^{''}\cdot\gamma)(\gamma\cdot\psi^{''}) \\&\quad\quad+ (\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\gamma)(\gamma\cdot\psi)+(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)(\gamma\cdot\gamma)+(\gamma^{''}\cdot\gamma)(\gamma\cdot\psi^{''})(\gamma\cdot\gamma)dt\end{aligned} K(γ+δψ)−K(γ)=∫t1tN2δ[γ′′−(γ′′⋅γ)γ][ψ′′−(γ′′⋅γ)ψ−(γ′′⋅ψ)γ−(ψ′′⋅γ)γ)]dt=2δ∫t1tNγ′′⋅ψ′′−(γ′′⋅γ)(γ′′⋅ψ)−(γ′′⋅ψ)(γ′′⋅γ)−(γ⋅ψ′′)(γ′′⋅γ)−(γ′′⋅γ)(γ⋅ψ′′)+(γ′′⋅γ)(γ′′⋅γ)(γ⋅ψ)+(γ′′⋅γ)(γ′′⋅ψ)(γ⋅γ)+(γ′′⋅γ)(γ⋅ψ′′)(γ⋅γ)dt由于 γ \gamma γ在四元数单位圆 H 1 H_{1} H1上,因此 γ ⋅ γ = ∥ γ ∥ 2 = 1 \gamma\cdot\gamma=\left \| \gamma \right \|^{2}=1 γ⋅γ=∥γ∥2=1,同时将公式(4.4)的结论 γ ⋅ ψ = − δ 2 ∥ ψ ∥ 2 \gamma \cdot \psi = -\frac{\delta}{2}\left \| \psi \right \|^{2} γ⋅ψ=−2δ∥ψ∥2代入上述表达式中,我们得到: K ( γ + δ ψ ) − K ( γ ) = 2 δ ∫ t 1 t N γ ′ ′ ⋅ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ + γ ⋅ ψ ′ ′ ) + ( γ ′ ′ ⋅ γ ) 2 ( − δ 2 ∥ ψ ∥ 2 ) d t = 2 δ ∫ t 1 t N γ ′ ′ ⋅ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ + γ ⋅ ψ ′ ′ ) d t \begin{aligned} K(\gamma+\delta \psi)-K(\gamma) &= 2\delta\int_{t_{1}}^{t_{N}}\gamma^{''}\cdot\psi^{''}-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi+\gamma\cdot\psi^{''})+(\gamma^{''}\cdot\gamma)^{2}( -\frac{\delta}{2}\left \| \psi \right \|^{2})dt \\&= 2\delta\int_{t_{1}}^{t_{N}}\gamma^{''}\cdot\psi^{''}-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi+\gamma\cdot\psi^{''})dt\end{aligned} K(γ+δψ)−K(γ)=2δ∫t1tNγ′′⋅ψ′′−(γ′′⋅γ)(γ′′⋅ψ+γ⋅ψ′′)+(γ′′⋅γ)2(−2δ∥ψ∥2)dt=2δ∫t1tNγ′′⋅ψ′′−(γ′′⋅γ)(γ′′⋅ψ+γ⋅ψ′′)dt同样省略被 δ 2 \delta^{2} δ2乘的项。经过多次改写,我们将 δ \delta δ分离单独作为一个因素。当除以 δ \delta δ时,这个因子将消失在导数的表达式中。因此,我们现在想分离出包含 ψ \psi ψ的项,使用分部积分和公式(4.3)的结论,表达式被重写如下: K ( γ + δ ψ ) − K ( γ ) = 2 δ ∑ i = 1 N − 1 L i \begin{aligned} K(\gamma+\delta \psi)-K(\gamma) &= 2\delta \sum_{i=1}^{N-1}L_{i}\end{aligned} K(γ+δψ)−K(γ)=2δi=1∑N−1Li其中 L i = ∫ t i t i + 1 γ ′ ′ ⋅ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ + γ ⋅ ψ ′ ′ ) d t = ∫ t i t i + 1 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ′ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) d t = [ ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ] t i t i + 1 − ∫ t i t i + 1 ( d d t ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ) ⋅ ψ ′ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) d t = [ ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ] t i t i + 1 − [ ( d d t ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ) ⋅ ψ ] t i t i + 1 + ∫ t i t i + 1 ( d 2 d t 2 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ) ⋅ ψ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) d t \begin{aligned} L_{i} &= \int_{t_{i}}^{t_{i+1}}\gamma^{''}\cdot\psi^{''}-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi+\gamma\cdot\psi^{''})dt \\&= \int_{t_{i}}^{t_{i+1}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{''}-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)dt \\&= [(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{'}]_{t_{i}}^{t_{i+1}} - \int_{t_{i}}^{t_{i+1}}(\frac{d}{dt}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma))\cdot\psi^{'}-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)dt \\&= [(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{'}]_{t_{i}}^{t_{i+1}} - [(\frac{d}{dt}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma))\cdot\psi]_{t_{i}}^{t_{i+1}} \\& \quad\quad+\int_{t_{i}}^{t_{i+1}}(\frac{d^{2}}{dt^{2}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma))\cdot\psi-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)dt\end{aligned} Li=∫titi+1γ′′⋅ψ′′−(γ′′⋅γ)(γ′′⋅ψ+γ⋅ψ′′)dt=∫titi+1(γ′′−(γ′′⋅γ)γ)⋅ψ′′−(γ′′⋅γ)(γ′′⋅ψ)dt=[(γ′′−(γ′′⋅γ)γ)⋅ψ′]titi+1−∫titi+1(dtd(γ′′−(γ′′⋅γ)γ))⋅ψ′−(γ′′⋅γ)(γ′′⋅ψ)dt=[(γ′′−(γ′′⋅γ)γ)⋅ψ′]titi+1−[(dtd(γ′′−(γ′′⋅γ)γ))⋅ψ]titi+1+∫titi+1(dt2d2(γ′′−(γ′′⋅γ)γ))⋅ψ−(γ′′⋅γ)(γ′′⋅ψ)dt注意,上面的表达式要求它是四阶可微的。现在我们可以使用 ψ \psi ψ在所有控制点上为零的公式(4.3),可以看到第二项为零,于是得到: L i = [ ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ] t i t i + 1 + ∫ t i t i + 1 ( d 2 d t 2 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ) ⋅ ψ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) d t \begin{aligned} L_{i} &= [(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{'}]_{t_{i}}^{t_{i+1}} +\int_{t_{i}}^{t_{i+1}}(\frac{d^{2}}{dt^{2}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma))\cdot\psi-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)dt\end{aligned} Li=[(γ′′−(γ′′⋅γ)γ)⋅ψ′]titi+1+∫titi+1(dt2d2(γ′′−(γ′′⋅γ)γ))⋅ψ−(γ′′⋅γ)(γ′′⋅ψ)dt再次考虑整个表达式: K ( γ + δ ψ ) − K ( γ ) = 2 δ ∑ i = 1 N − 1 L i = 2 δ ∑ i = 1 N − 1 [ ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ] t i t i + 1 + 2 δ ∑ i = 1 N − 1 ∫ t i t i + 1 ( d 2 d t 2 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ) ⋅ ψ − ( γ ′ ′ ⋅ γ ) ( γ ′ ′ ⋅ ψ ) d t = 2 δ [ ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ] t 1 t N + 2 δ ∑ i = 1 N − 1 ∫ t i t i + 1 ( d 2 d t 2 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) − ( γ ′ ′ ⋅ γ ) γ ′ ′ ) ⋅ ψ d t \begin{aligned} K(\gamma+\delta \psi)-K(\gamma) &= 2\delta \sum_{i=1}^{N-1}L_{i} \\&= 2\delta\sum_{i=1}^{N-1}[(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{'}]_{t_{i}}^{t_{i+1}} + 2\delta\sum_{i=1}^{N-1}\int_{t_{i}}^{t_{i+1}}(\frac{d^{2}}{dt^{2}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma))\cdot\psi-(\gamma^{''}\cdot\gamma)(\gamma^{''}\cdot\psi)dt \\&= 2\delta[(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{'}]_{t_{1}}^{t_{N}} + 2\delta\sum_{i=1}^{N-1}\int_{t_{i}}^{t_{i+1}}(\frac{d^{2}}{dt^{2}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)-(\gamma^{''}\cdot\gamma)\gamma^{''})\cdot\psi dt \end{aligned} K(γ+δψ)−K(γ)=2δi=1∑N−1Li=2δi=1∑N−1[(γ′′−(γ′′⋅γ)γ)⋅ψ′]titi+1+2δi=1∑N−1∫titi+1(dt2d2(γ′′−(γ′′⋅γ)γ))⋅ψ−(γ′′⋅γ)(γ′′⋅ψ)dt=2δ[(γ′′−(γ′′⋅γ)γ)⋅ψ′]t1tN+2δi=1∑N−1∫titi+1(dt2d2(γ′′−(γ′′⋅γ)γ)−(γ′′⋅γ)γ′′)⋅ψdt利用控制点的连续性进行最后改写,我们可以求出“导数”: lim δ → 0 K ( γ + δ ψ ) − K ( γ ) δ = 2 [ ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) ⋅ ψ ′ ] t 1 t N + 2 ∑ i = 1 N − 1 ∫ t i t i + 1 ( d 2 d t 2 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) − ( γ ′ ′ ⋅ γ ) γ ′ ′ ) ⋅ ψ d t (4.5) \begin{aligned} \lim_{\delta\rightarrow 0}\frac{K(\gamma+\delta \psi)-K(\gamma)}{\delta} &= 2[(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)\cdot\psi^{'}]_{t_{1}}^{t_{N}} \\&+ 2\sum_{i=1}^{N-1}\int_{t_{i}}^{t_{i+1}}(\frac{d^{2}}{dt^{2}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma)-(\gamma^{''}\cdot\gamma)\gamma^{''})\cdot\psi dt \tag{4.5}\end{aligned} δ→0limδK(γ+δψ)−K(γ)=2[(γ′′−(γ′′⋅γ)γ)⋅ψ′]t1tN+2i=1∑N−1∫titi+1(dt2d2(γ′′−(γ′′⋅γ)γ)−(γ′′⋅γ)γ′′)⋅ψdt(4.5)由于 γ ⋅ γ = ∥ γ ∥ = 1 \gamma\cdot\gamma=\left \| \gamma \right \|=1 γ⋅γ=∥γ∥=1,所以有: 0 = ( 1 ) ′ ′ = ( γ ⋅ γ ) ′ ′ = 2 γ ′ ′ ⋅ γ + 2 γ ′ ⋅ γ ′ (4.6) 0=(1)^{''}=(\gamma\cdot\gamma)^{''}=2\gamma^{''}\cdot\gamma+2\gamma^{'}\cdot\gamma^{'}\tag{4.6} 0=(1)′′=(γ⋅γ)′′=2γ′′⋅γ+2γ′⋅γ′(4.6)由于在控制点处对任意 ψ \psi ψ的导数必须为零(方程4.3),结合方程4.6,我们对解有以下要求: γ ∈ C 4 ( ( I ) , H 1 ) 0 = γ ′ ′ ( t 1 ) − ( γ ′ ′ ( t 1 ) ⋅ γ ( t 1 ) ) γ ( t 1 ) 0 = γ ′ ′ ( t N ) − ( γ ′ ′ ( t N ) ⋅ γ ( t N ) ) γ ( t N ) ( γ ′ ′ ⋅ γ ) γ ′ ′ = d 2 d t 2 ( γ ′ ′ − ( γ ′ ′ ⋅ γ ) γ ) = γ ′ ′ ′ ′ − ( γ ′ ′ ⋅ γ ) ′ ′ γ − 2 ( γ ′ ′ ⋅ γ ) ′ γ ′ − ( γ ′ ′ ⋅ γ ) γ ′ ′ ⇒ 0 = γ ′ ′ ′ ′ + ( γ ′ ⋅ γ ′ ) ′ ′ γ + 2 ( γ ′ ⋅ γ ′ ) ′ γ ′ + 2 ( γ ′ ⋅ γ ′ ) γ ′ ′ \begin{aligned} \gamma & \in C^{4}((I),H_{1}) \\ 0 &= \gamma^{''}(t_{1})-(\gamma^{''}(t_{1})\cdot\gamma(t_{1}))\gamma(t_{1}) \\ 0 &= \gamma^{''}(t_{N})-(\gamma^{''}(t_{N})\cdot\gamma(t_{N}))\gamma(t_{N}) \\ (\gamma^{''}\cdot\gamma)\gamma^{''} &= \frac{d^{2}}{dt^{2}}(\gamma^{''}-(\gamma^{''}\cdot\gamma)\gamma) \\&= \gamma^{''''}-(\gamma^{''}\cdot\gamma)^{''}\gamma-2(\gamma^{''}\cdot\gamma)^{'}\gamma^{'}-(\gamma^{''}\cdot\gamma)\gamma^{''} \\ \Rightarrow 0&= \gamma^{''''}+(\gamma^{'}\cdot\gamma^{'})^{''}\gamma+2(\gamma^{'}\cdot\gamma^{'})^{'}\gamma^{'}+2(\gamma^{'}\cdot\gamma^{'})\gamma^{''} \end{aligned} γ00(γ′′⋅γ)γ′′⇒0∈C4((I),H1)=γ′′(t1)−(γ′′(t1)⋅γ(t1))γ(t1)=γ′′(tN)−(γ′′(tN)⋅γ(tN))γ(tN)=dt2d2(γ′′−(γ′′⋅γ)γ)=γ′′′′−(γ′′⋅γ)′′γ−2(γ′′⋅γ)′γ′−(γ′′⋅γ)γ′′=γ′′′′+(γ′⋅γ′)′′γ+2(γ′⋅γ′)′γ′+2(γ′⋅γ′)γ′′其中第二个和第三个要求等价于端点处的局部曲率为零。
综上所述,现在我们可以找到一组微分方程,当它有解时就能找到理想的最优插值曲线的解析解:
给定控制点 q 1 , . . . , q N ∈ H 1 q_{1},...,q_{N}\in H_{1} q1,...,qN∈H1,插值曲线 γ ∈ C 4 ( I , H 1 ) \gamma \in C^{4}(I,H_{1}) γ∈C4(I,H1),对于 t i ∈ I t_{i}\in I ti∈I有 γ ( t i ) = q i \gamma(t_{i})=q_{i} γ(ti)=qi,当 γ \gamma γ满足一下要求时,将使 ∫ t 1 t N ∥ κ ( h ) ∥ 2 d t \int_{t_{1}}^{t_{N}}\left \| \kappa (h) \right \|^{2}dt ∫t1tN∥κ(h)∥2dt最小化:
- κ ( t 1 ) = 0 \kappa(t_{1})=0 κ(t1)=0
- κ ( t N ) = 0 \kappa(t_{N})=0 κ(tN)=0
- 对于每个间隔 t i < t < t i + 1 t_{i}<t<t_{i+1} ti<t<ti+1有: γ ′ ′ ′ ′ + ( γ ′ ⋅ γ ′ ) ′ ′ γ + 2 ( γ ′ ⋅ γ ′ ) ′ γ ′ + 2 ( γ ′ ⋅ γ ′ ) γ ′ ′ = 0 \gamma^{''''}+(\gamma^{'}\cdot\gamma^{'})^{''}\gamma+2(\gamma^{'}\cdot\gamma^{'})^{'}\gamma^{'}+2(\gamma^{'}\cdot\gamma^{'})\gamma^{''}=0 γ′′′′+(γ′⋅γ′)′′γ+2(γ′⋅γ′)′γ′+2(γ′⋅γ′)γ′′=0
现在“所有”剩下的工作就是用给定的边界值来解决上述四阶微分方程。不幸的是,这在现有的数学知识中是不可能的。这是由Jorgen Sand(哥本哈根大学计算机科学学院系统方程求解专业副教授)和Gerd Grubb(哥本哈根大学数学学院微分方程专业教授)确认的。
5. 正切曲率 κ ( γ , t ) \kappa(\gamma, t) κ(γ,t)在 H 1 H_{1} H1上的连续半解析解
上边是理想最优插值曲线在不可解微分方程上的严格数学推导。然而,我们可以再次在平面中寻找灵感。对应的微分方程是 γ ′ ′ ′ ′ \gamma^{''''} γ′′′′=0,即曲线的四阶导数在控制点之间必须为零,这对应于三阶曲线(样条)。如果解被约束为三阶曲线,则方程组求解起来会比较容易。
因此,我们可以限制我们希望插值曲线属于哪一类函数。例如,这可以是一种三次样条。在此限制下,优化问题得以解决。
根据曲线类定义的选择,这种寻找解决方案的策略将给出与构建Squad基础相对应的结果。为了使此系列博客保持在可管理的范围内,我们将不再进一步探讨这一思路。
本文总结:本节引入最优插值的求解理念,并给出连续解析解的详细证明过程,限于篇幅,只是对连续半解析解进行介绍,感兴趣的童鞋可以自行求证。下一篇将介绍最优插值曲线的离散数值解Spring的解、证明和图像演示。
本文相对于原文会适当精简,同时为便于全面理解,会收集其他网络好文,根据作者理解,加入一些注解和扩展知识点,如果您觉得还不错,请一键四连(点赞关注收藏评论),让更多的人看到。
参考文献:
- 《视觉SLAM十四讲:从理论到实践》,高翔、张涛等著,中国工信出版社
- Quaternions, Interpolation and Animation
- 变分法入门介绍
- 什么是曲率和曲率半径?