开始学习之前，先介绍一下什么是刚体：在运动中和受力作用后，形状和大小不变，内部各点相对位置不变的物体。

在三维空间中考虑刚体，它不仅有位置，还有自身的姿态。相机（SLAM中最重要的设备）也可以看成三维空间的刚体，位置是指相机在空间中的哪个地方，而姿态则是指相机的朝向。

旋转矩阵

先从最基本的内容学习：点和向量。

点的几何意义很好理解。向量怎么理解呢？它是线性空间中的一个元素，可以把它想象成从原点指向某处的一个箭头。需要注意的是，不要把向量和向量的坐标这两个概念混淆。一个向量是空间当中的一样东西，比如说 $\vec{a}$ ，这个时候 $\vec{a}$ 并不是和若干个实数相关联的，因为 $\vec{a}$ 不知道它处于哪个参考坐标系中。只有当我们指定这个三维空间中的某个坐标系时，才可以讨论 $\vec{a}$ 在此坐标系下的坐标，也就是找到了若干个实数来对应这个向量。

下面介绍几个常见的线性代数中关于向量的计算公式：对与 $\vec{a},\vec{b}$ $\epsilon$ $R^{3}$

内积： $\vec{a}\cdot \vec{b}=\vec{a}^{T}\vec{b}=\sum_{i=1}^{3}a_{i}b_{i}=|\vec{a}||\vec{b}| cos<\vec{a},\vec{b}>$
外积： $\vec{a}\times \vec{b}=\begin{Vmatrix} \vec{i} & \vec{j}& \vec{k}\\ a_{1} & a_{2} &a_{3} \\ b_{1}&b_{2} & b_{3} \end{Vmatrix}=\begin{bmatrix} a_{2}b_{3}-a_{3}b_{2}\\ a_{3}b_{1}-a_{1}b_{3}\\ a_{1}b_{2}-a_{2}b_{1} \end{bmatrix}= \begin{bmatrix} 0& -a_{3}& a_{2}\\ a_{3}&0 &-b_{1} \\ -a_{2}&a_{1} &0 \end{bmatrix}\vec{b}\doteq\vec{a}^\Lambda \vec{b}$ 。外积的方向垂直于这两个向量所在的平面，大小为 $\begin{vmatrix} \vec{a} \end{vmatrix} \begin{vmatrix} \vec{b} \end{vmatrix} \sin <\vec{a},\vec{b}>$ ，是这两个向量张成的平行四边形的有向面积。

重点：外积只对三维向量存在定义，我们还可以用外积来表示向量的旋转。外积如何来表示旋转呢？

考虑两个不平行的向量 $\vec{a},\vec{b}$ ，我们来描述从 $\vec{a}$ 到 $\vec{b}$ 是如何旋转的？

实际上，我们也是用向量来表示从 ${\color{Red} \vec{a}}$ 到 ${\color{Red} \vec{b}}$ 的旋转关系的。在右手法则下，我们用右手的四个手指从 ${\color{Red} \vec{a}}$ 握向 ${\color{Red} \vec{b}}$ ，大拇指的朝向就是旋转向量的方向，事实上这就是 ${\color{Red} \vec{a}\times \vec{b}}$ 的方向。旋转向量的大小由 ${\color{Red} \vec{a}}$ 和 ${\color{Red} \vec{b}}$ 的夹角决定。

通过这样的方式，我们构造了从 $\vec{a}$ 到 $\vec{b}$ 的一个旋转向量，这个向量同样位于三维空间中，在此坐标系下，可以用3个实数来描述。

下面来看一下坐标系间的欧式变换

与向量间的旋转类似，同样可以描述两个坐标系之间的旋转关系。坐标系之间的旋转关系+平移关系，统称为坐标系之间的变换关系。

先来看下面这个场景。

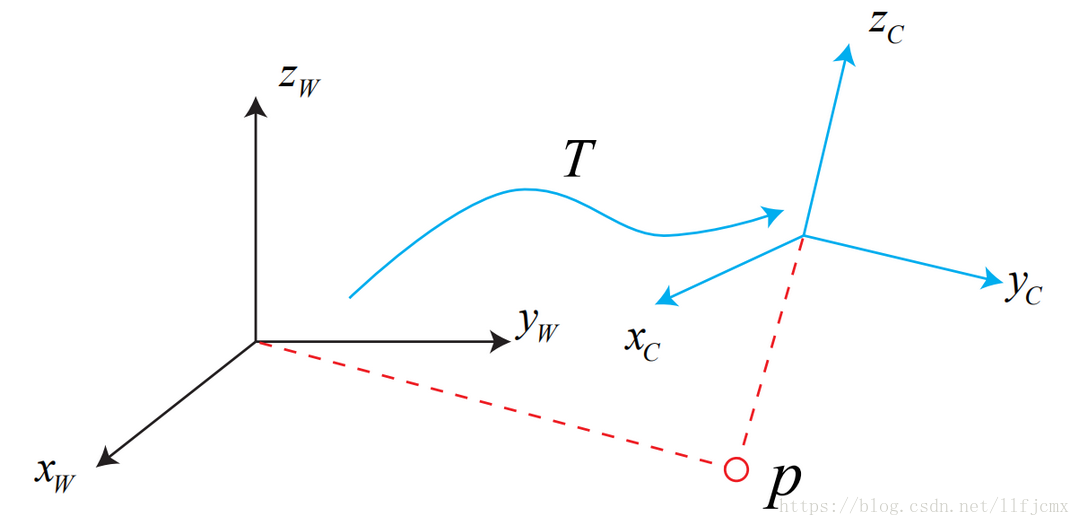
在机器人的运动过程中，常见的做法是设定一个惯性坐标系（也可以称为世界坐标系），可以认为它是固定不动的。同时，相机（或者说机器人）则是一个移动坐标系。如下图：

扫描二维码关注公众号，回复： 3471585 查看本文章

$x_{w},y_{w},z_{w}$ 定义的坐标系是世界坐标系， $x_{c},y_{c},z_{c}$ 定义的坐标系是移动坐标系

现在有这么一个问题了：假设在相机视野中某个向量 $\vec{p}$ ，它的坐标为 $\vec{p}_{c}$ ，在世界坐标系下面看，它的坐标是 $\vec{p}_{w}$ ，这两个坐标之间是如何转换的呢？

这就是这一小节要研究的问题了。

整体思路：先得到该点针对移动坐标系的坐标值，再根据机器人位姿转换到世界坐标系中，这个转换关系可以用一个矩阵 $T$ 来描述。

欧式变换：相机运动是一个刚体运动，它保证了一个向量在各个坐标系下的长度和夹角都不会发生变化，这种变换就是~。

想象一下：如果把手机抛到空中，在手机落地摔碎之前，只可能有空间位置和姿态的变化，而手机的长度、各个面的角度这些性质都不会发生变化。

这样一个欧式变换由一个旋转和一个平移组成。

下面来寻找变换关系：

首先考虑旋转关系：

我们设某个单位正交基 $(\vec{e_{1}},\vec{e_{2}},\vec{e_{3}})$ ，经过旋转变成了 $(\vec{e_{1}^{'}},\vec{e_{2}^{'}},\vec{e_{3}^{'}})$ 。

那么，对于同一个向量 $\vec{a}$ （注意它没有因为坐标系的旋转而发生变化），设它在两个坐标系的坐标分别为 $(a_{1},a_{2},a_{3})$ 和 $(a_{1}^{'}, a_{2}^{'},a_{3}^')$ 。

根据坐标的定义，有下列关系： $a_{1}\vec{e1}+a_{2}\vec{e2}+a_{3}\vec{e3}=a_{1}^{'}\vec{e_{1}^{'}}+a_{2}^{'}\vec{e_{2}^{'}}+a_{3}^{'}\vec{e_{3}^{'}}$

写成矩阵的形式就是： $(\vec{e_{1}},\vec{e_{2}},\vec{e_{3}})\bigl(\begin{smallmatrix} a_{1}\\ a_{2}\\ a_{3} \end{smallmatrix}\bigr) = (\vec{e_{1}^{'}},\vec{e_{2}^{'}},\vec{e_{3}^{'}})\bigl(\begin{smallmatrix} a_{1}^{'}\\ a_{2}^{'}\\ a_{3}^{'} \end{smallmatrix}\bigr)$