SLAM十四讲：三维空间刚体运动(3)

内容总览：旋转矩阵的推导，变换矩阵的推导

旋转矩阵

向量的表达需要依附在空间坐标系中，如一个线性空间的基为 $(e_1,e_2,e_3)$，那么 $a$在这个坐标系中的坐标：

公式1

$\$

一般来讲，都用右手系。

对于 $a,b \in \R^3$，内积可以描述向量间的投影关系：

外积：

^表示反对称矩阵，所以上式也写成了矩阵乘法： $a$ ^ $b$

外积得到的是一个新的向量，方向和 $a,b$都垂直，大小由 $a,b$间的夹角决定： $|a||b|sin<a,b>$，所以也可以用来表示旋转，如下图所示， $w$就是外积

坐标系间的欧氏变换

刚体运动在各个坐标系下的长度和夹角都不会发生变化，这种变换成为欧式变换，包括旋转和平移。

上面提到，向量只有在坐标系中才有意义:
现在一个单位正交基 $(e_1,e_2,e_3)$，旋转后变成了 $(e'_1,e'_2,e'_3)$，对于一个一开始就存在的、并未随着坐标系而旋转的向量 $a$，在两个坐标系中的坐标分别是 $[a_1,a_2,a_3]^T$和 $[a'_1,a'_2,a'_3]^T$，那么根据公式1， $a$为：

若想得到 $a_1$到 $a'_1$的变化，就两边同时左乘 $[e^T_1,e^T_2.e^T_3]^T$,就得到：

中间这一块就是旋转矩阵 $R$，能表现出向量 $a$在不同空间坐标系中的坐标变化关系，也能描述相机的旋转。
旋转矩阵集合：

旋转矩阵是一个正交矩阵，所以旋转矩阵的逆可以描述相反的旋转

加上一个平移向量 $t$，就是一个完整的欧式变换：

$\$

欧式变换与齐次坐标

但如果多次变换之后还用这种公式，就会很繁琐，因此引入矩阵写法：

注意，在这里，把一个三维向量的末尾添加了1，成了四维向量，变成了齐次坐标，这么做是出于方便线性计算的考虑，能将旋转和平移放到一起计算。
原理：在齐次坐标中，某个点的每个分量同乘一个非零常数 k 后， 仍然表示的是同一个点。这个可能可以用四维空间的概念去理解，按照刘慈欣的《三体》中的说法，四维空间的生命看三维空间的人，就像是三维空间中的人看纸片上的人，一个纸片上的点，在一个他表示不出的z维度上，无论放大多少非零倍，他的位置也是不变的，同理，一个三维上的点，在表示不出的某四维维度上，无论放大多少非零倍，也是不变的，只要将放大的倍数置为1，那么前三个数值就是三位空间中的数值。

至此，两次累加就可以写成 $c = T_1T_2a$

再看变换矩阵T的结构：左上角为旋转矩阵，右侧为平移向量，左
下角为 0 向量，右下角为 1。这种矩阵又称为特殊欧氏群（Special Euclidean Group）：

同上旋转矩阵，可以直接求逆表示反向变换：

旋转向量和欧拉角

旋转向量

任何的旋转都可以用一个旋转轴和一个旋转角来表示，因此使用一个向量，长度等于旋转角 $\theta$，方向和旋转轴一致 $n$，这个向量就是旋转向量。

研究旋转向量的原始想要更紧凑的表达， 旋转矩阵的有9个量，但只有3个自由度，这种表达方式有些冗余

旋转向量到旋转矩阵(Rodrigues’s Formula)：

旋转矩阵到旋转向量：
$\theta$推导：

$n$推导：
旋转轴上的向量在旋转后不发生变化，所以 $Rn=n$， $n$就是 $R$的特征值为1的特征向量，归一化后得到旋转轴。

欧拉角

三个分离的转角，把旋转分解成三次绕不同轴的旋转：

但是欧拉角存在万向锁的缺陷：当 $y$为+90°或-90°时，第一次和第三次旋转用的同一个轴。

作用：用欧拉角来验证算法是否出错

四元数

概念：
四元数是一种即紧凑，又没有奇异性的三维空间旋转表达方法。

结构：
一个四元数 $q$拥有一个实部和三个虚部:
$q = q_0 + q_1i + q_2j + q_3k$
三个虚部满足关系：

另一种表达方式：

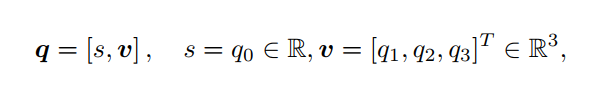
这里， s 称为四元数的实部，而 v 称为它的虚部。如果一个四元数虚部为 0，称之为实四
元数。反之，若它的实部为 0，称之为虚四元数。

四元数和旋转向量的关系：
设单位向量 $n = [n_x,n_y,n_z]^T$，进行了角度为 $\theta$的旋转，则旋转向量到四元数：

四元数到旋转向量：

四元数的运算等有需要了再整理

相似、仿射、射影变换