机械臂运动控制——三维空间刚体运动描述

一、旋转矩阵

在机器人运动的过程当中，我们通常会设定一个惯性坐标系（或者叫世界坐标系），姑且认为这个坐标系是固定不动的。例如： $X_w$ , $Y_w$ , $Z_w$ 是固定不动的世界坐标系， $X_c$ , $Y_c$ , $Z_c$ 是机器人坐标系。存在一个向量 $P$ ，在世界坐标系下的坐标是 $P_w$ ，在移动机器人坐标系下的坐标是 $P_c$ ，通常情况下，我们通过传感器已知移动机器人坐标系统下的坐标 $P_c$ ，来求 $P$ 在世界坐标系下的坐标 $P_w$

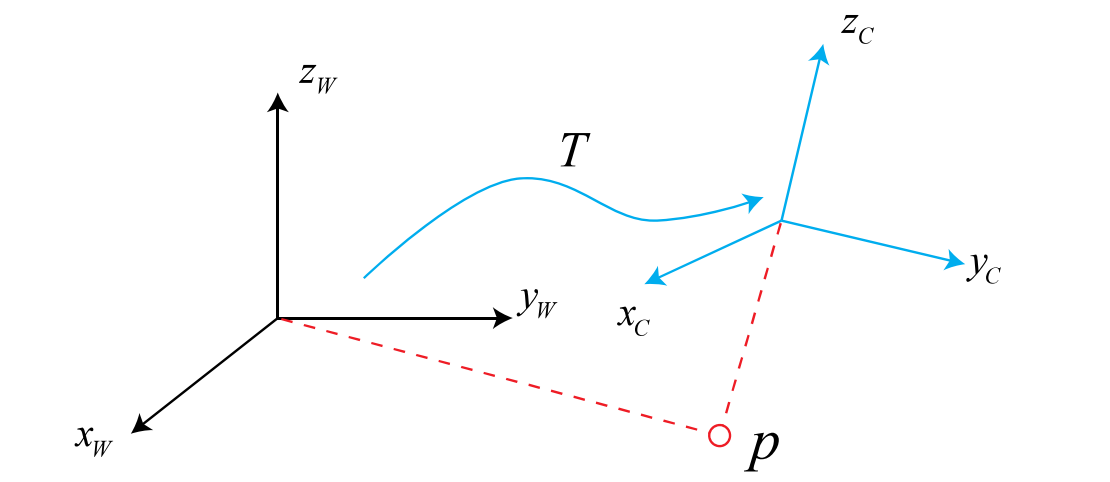
为了求 $P_w$ ，我们必须知道机器人坐标系 $X_c$ , $Y_c$ , $Z_c$ 相对与世界坐标 $X_w$ , $Y_w$ , $Z_w$ 做了哪些变换。我们定义世界坐标系经过变换矩阵 $T$ 之后得到机器人坐标系（这可以通过计算里程和IMU的数据进行测量出来）（这也就说明了为什么在机器人刚刚启动的时候odom和base_link坐标系必须是重合的，不然没有办法计算旋转矩阵），另外一般情况下，移动机器人运动是一个刚体运动，也就是说机器人的形状和大小不会因为坐标系不同而改变，这种变换叫做欧式变换。一个欧式变换可以由旋转和平移两个部分组成。首先我们考虑旋转问题，假设在世界坐标系下的单位正交基 $(e_x,e_y,e_z)$ ，在移动机器人坐标系下的单位正交基 $(e{_{x}^{''}},e{_{y}^{''}},e{_{z}^{''}})$ ，那么，根据向量 $P$ 的模可知：

$[e{_{x}},e{_{y}},e{_{z}}]\cdot P_{W}^{T} =[e{_{x}^{''}},e{_{y}^{''}},e{_{z}^{''}}]\cdot P_{C}^{T}$

因此， $P_{C}^{T}=[e_x,e_y,e_z]^T\cdot [e_{x}^{''},e_{y}^{''},e_{z}^{''}]\cdot P_{W}^{T}$ ，我们将 $[e_x,e_y,e_z]^T\cdot [e_{x}^{''},e_{y}^{''},e_{z}^{''}]$ 记做旋转矩阵 $R$ ，因此上面的表达式可以简化为 $P_{C}^{T}=R\cdot P_{W}^{T}$ 。接下来是平移部分，假设平移部分是 $P_{C^{''}}^{T}$ 经过平移向量 $t$ 后得到 $P_{C}^{T}$ ，那么可以得到 $P_{C}^{T}=P_{C^{''}}^{T}+t=R\cdot P_{W}^{T}+t$ 。所以通过旋转矩阵 $R$ 和平移向量 $t$ ，我们可以描述从世界坐标系到移动机器人坐标系的坐标变换。但是这种表达方式存在一个问题，对于连续的位置变换，例如机器人坐标系是随着时间在不断变换的，上面这种表达方式并不是一个线性的表达方式，假设我们经历了两次变换 $R_1$ , $t_1$ 和 $R_2$ , $t_2$ 且满足：从 $a$ 到 $b$ 的变换 $b=R_1a+t_1$ ，从 $b$ 到 $c$ 的变换 $c=R_2b+t_2$ ，那么从 $a$ 到 $c$ 的变换是 $c=R_2(R_1a+t_1)+t_2$ .并不是我们希望的的形式 $c=R_a+t$ (然后我们采用齐次坐标的方式进行表达，详细的部分参考李群李代数).

二、欧拉角

旋转本身就是一个很直观的现象。欧拉角可以提供一种非常直观的方式。他利用3个分离的转角，把一次旋转分解成3次绕不同的轴进行旋转。例如先绕x轴旋转，再绕y轴旋转，最后绕z轴旋转，这样就得到一个xyz轴的旋转。在欧拉角中一个常用的是“航偏-俯仰-翻滚”（yaw-pitch-roll）。可以简单记忆rpy-xyz。其中roll-对应着绕x轴旋转后的翻滚角。Pitch对应着绕y轴旋转后的俯仰值，yawd对应着绕z轴旋转后的航偏值。那么旋转部分就可以通过roll-pitch-yaw这三个量来描述。

在使用欧拉角这种表达方式的时候，会存在万象锁的问题。也就是一旦旋转pitch为90度，就会导致第一次旋转和第三次转换等价，丢失了一个表示维度。万象锁现象如下图所示

三、四元数

旋转矩阵用9个量来描述3自由度的旋转，具有冗余性；欧拉角虽然用3个量来描述3自由度的旋转，但是具有万向锁的问题，因此我们选择用四元数，（ROS当中描述转向的都是采用的四元数）。一个四元数拥有一个实部和三个虚部组成。

三个虚部满足以下关系

写成矩阵的样子就是 $q=[w,x,y,z]^T$ ，其中 $|q|^2 = w^2=x^2+y^2+z^2 =1$ ，从欧拉角到四元数的公式：

从四元数转化到欧拉角公式

四、不同运动描述转换的程序实现

C++（转自https://blog.csdn.net/zhuoyueljl/article/details/70789472）

//欧拉角转换到四元数
Eigen::Quaterniond euler2Quaternion(double roll, double pitch, double yaw)  
{  
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());  
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());  
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());  
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;  
    return q;  
}

//四元数转换到欧拉角
  Eigen::Vector3d Quaterniond2Euler(const double x,const double y,const double z,const double w)  
{  
    Eigen::Quaterniond q;  
    q.x() = x;  
    q.y() = y;  
    q.z() = z;  
    q.w() = w;   
    Eigen::Vector3d euler = q.toRotationMatrix().eulerAngles(2, 1, 0);
    return euler;  
}

//旋转矩阵转换到四元数
  Eigen::Quaterniond rotationMatrix2Quaterniond(Eigen::Matrix3d R)  
{  
    Eigen::Quaterniond q = Eigen::Quaterniond(R); 
    q.normalize();  
    return q;  
}  

//四元数转换到旋转矩阵
Eigen::Matrix3d Quaternion2RotationMatrix(const double x,const double y,const double z,const double w)  
{  
    Eigen::Quaterniond q;  
    q.x() = x;  
    q.y() = y;  
    q.z() = z;  
    q.w() = w;    
    Eigen::Matrix3d R = q.normalized().toRotationMatrix();  
    return R;  
}  

//欧拉角转换到旋转矩阵
Eigen::Matrix3d euler2RotationMatrix(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    Eigen::Matrix3d R = q.matrix();
    return R;
}

//旋转矩阵转换到欧拉角
Eigen::Vector3d RotationMatrix2euler(Eigen::Matrix3d R)
{
    Eigen::Matrix3d m;
    m = R;
    Eigen::Vector3d euler = m.eulerAngles(0, 1, 2);
    return euler;
}

参考

https://www.cnblogs.com/21207-iHome/p/6894128.html

https://blog.csdn.net/zhuoyueljl/article/details/70789472

中国大学MOOC———《机器人操作系统入门》