三维空间刚体运动2：旋转向量表示旋转

本篇继续参照高翔老师《视觉SLAM十四讲从理论到实践》，讲解三维空间刚体运动。博文将原第三讲分为四部分来讲解：1、旋转矩阵和变换矩阵；2、旋转向量表示旋转；3、欧拉角表示旋转；4、四元数表示变换。本文相对于原文会适当精简，同时为便于理解，会加入一些注解和补充知识点，本篇为第二部分：旋转向量表示旋转，另外三部分请参照博主的其他博文。

1.定义

对于矩阵表示方式至少有以下两个缺点：
1. $SO(3)$的旋转矩阵有9个量，但一次旋转只有3个自由度，因此这种表达方式是冗余的，同理 $SE(4)$也是。那么，是否有更紧凑的表示呢？
2.旋转矩阵和变换矩阵自身带有约束：它必须是正交矩阵且行列式为。当想估计或优化一个旋转矩阵或变换矩阵时，这些约束会使得求解变的更困难。
因此，希望有一种方式能够紧凑的描述旋转和平移。

旋转向量：事实上，任意旋转都可以用一个旋转轴和一个旋转角来刻画，于是，我们可以使用一个向量，其方向 $n$与旋转轴一致，其长度等于旋转角 $\Theta$，那么向量 $\Theta n$也可以描述这个旋转，这种向量称为旋转向量（或轴角/角轴，Axis-Angle），只需一个三维向量即可描述旋转。同样，对于变换矩阵，使用一个旋转向量和一个平移向量即可表达一次变换，此时变量维数正好是六维。

2.罗德里格斯公式

2.1 定义

罗德里格斯公式：旋转向量和旋转矩阵有什么联系吗？事实上，从旋转向量到旋转矩阵的转换过程由罗德里格斯公式（Rodrigues’s Formula）表示。因为任意旋转都可以由一个旋转轴 $n$和一个旋转角 $\Theta$刻画，故罗德里格斯公式具体形式如下： $R= \cos \theta I+(1-\cos \theta )nn^{T}+\sin \theta n^{\wedge }\tag{1.1}$
符号 $^{\wedge }$是向量到反对称矩阵的转换符，见第一篇博客的公式（1.4）。

2.2 推导

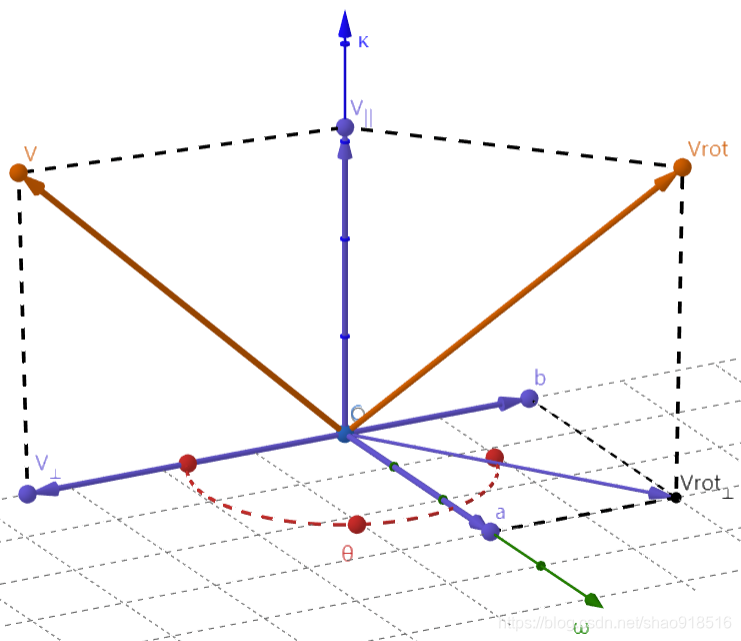
首先，理解图1。定义向量 $k$是旋转轴的单位矢量，为表示方便，使用 $k$代表 $n$。图中初始向量 $v$以 $k$为轴旋转角 $\theta$得到 $v_{rot}$。向量 $w$为 $k\times v$的方向上的单位向量，向量 $v_{\perp }$和 $v_{rot\perp }$分别是 $v$和 $v_{rot}$的垂直于平面的向量。向量 $a$和 $b$分别是 $v_{rot}$在 $w$和 $v_{\perp }$方向上的分量。
图1.1：旋转向量3D图（推荐数学绘图软件：geogebra）

所谓推导旋转方程，实则求出一个旋转矩阵，使得 $V_{rot}=Rv$，所以我们要做的就是找出 $v_{rot}$与 $v$，并用矩阵来表示。
此公式有2种形式，故而也有2种推导方法，两者推导方法的不同主要在 $v_{\perp }$的表示上。具体推导过程如下。

2.2.1 推导一

推导一使用单位向量 $k$表示，推导过程如下：

1. 对 $v$进行向量分解： $v = v_{\perp } + v_{||}$
2. 由点乘的投影几何意义可得： $v_{||}=(v\cdot k)k$，其中 $(v\cdot k)$为标量，所以再乘向量 $k$得到一个矢量
3. 根据向量减法可得： $v_{\perp } = v - v_{||}$
4. 由旋转过程平行向量不变得： $v_{rot||} = v_{||}$
5. 为计算方便，对 $v_{rot\perp}$ 进行向量分解： $v_{rot\perp} =a+b$
6. 由图中的向量关系经推导可得： $a=\sin \theta k\times v,b=\cos \theta v_{\perp }$， $a,b$的推导在后边
7. 综上可得：
   $v_{rot}=v_{rot\perp}+v_{rot||}$
            $=a+b+v_{||}$
            $=\sin \theta k\times v +\cos \theta v_{\perp } + (v\cdot k)k$
            $=\sin \theta k\times v +\cos \theta (v - v_{||}) + (v\cdot k)k$
            $=\sin \theta k\times v +\cos \theta (v - (v\cdot k)k ) + (v\cdot k)k$
            $=\cos \theta v+(1-\cos \theta )(v\cdot k)k + \sin \theta k\times v$
   显然：到此步，我们还无法将其用矩阵来表示，所以需要对 $(v\cdot k)k$ 和 $k\times v$ 进行矩阵转换，由点积的交换律和结合律得： $(v\cdot k)k=k\cdot(v\cdot k)=k\cdot (k^{T} v)=k\cdot k^{T} v$其中的向量都是列向量，点积展开规则为： $x\cdot y = [x, y] =x^{T}y$。
   对于 $k\times v$可用叉乘矩阵来化简为 $Kv$： $\begin{bmatrix} (k\times v)_{x}\\ (k\times v)_{y}\\ (k\times v)_{z} \end{bmatrix}= \begin{bmatrix} k_{y}v_{z}- k_{z}v_{y}\\ k_{z}v_{x}- k_{x}v_{z}\\ k_{x}v_{y}- k_{y}v_{x} \end{bmatrix}= \begin{bmatrix} 0 & -k_{z} & k_{y}\\ k_{z} & 0 & -k_{x}\\ k_{y} & k_{x} & 0 \end{bmatrix}\begin{bmatrix} v_{x}\\ v_{y}\\ v_{z} \end{bmatrix}= Kv$
   故 $v_{rot}=\cos \theta v+(1-\cos \theta )(v\cdot k)k + \sin \theta k\times v$
               $=\cos \theta v+(1-\cos \theta )kk^{T}v + \sin \theta K v$
               $=(\cos \theta I +(1-\cos \theta )kk^{T} + \sin \theta K )v$
   故旋转矩阵 $R= \cos \theta I +(1-\cos \theta )kk^{T} + \sin \theta K. \tag{1.2}$其中 $I$为单位矩阵。

2.2.2 推导二

与推导一相比，推导二的不同主要在于用叉乘去表示一些数据。用叉乘来表示v⊥可得： $v_{\perp } =-k\times (k\times v)$。
所以联立推导一中各式得：
$v_{rot}=v_{rot\perp}+v_{rot||}$
         $=a+b+v_{||}$
         $=\sin \theta k\times v +\cos \theta v_{\perp } + v-v_{\perp }$
         $=\sin \theta k\times v -\cos \theta k\times (k\times v) + v + k\times (k\times v)$
         $=v + (1 - \cos \theta )k\times (k\times v) + \sin \theta k\times v$
         $=v + (1 - \cos \theta )K^{2}v+ \sin \theta Kv$(叉乘矩阵表示)
         $=(I + (1 - \cos \theta )K^{2}+ \sin \theta K)v$
         $=Rv$
从而得出第二种表达式 $R= I +(1-\cos \theta )K^{2} + \sin \theta K. \tag{1.3}$显然，第二种表达式更为简便，在计算的过程中涉及的参数更少，所以这也是在进行旋转操作时常用的公式。

2.2.3 推导 $a$

向量 $a$和 $b$是由 $v_{rot\perp }$正交分解得到的矢量，既有大小又有方向，所以在求解时，我们要对其大小和方向分别求解。
大小
设 $\theta_{1}= \pi -\theta$， $\theta_{2}$是向量 $v$和 $k$的夹角， $k$为单位向量，则对于 $a$的大小 $|a|$有：
$|a|=\sin \theta_{1}|v_{rot\perp }|=\sin \theta_{1}|v_{\perp }|$
       $=\sin (\pi -\theta)|v_{\perp }|=\sin \theta|v_{\perp }|$
       $=\sin \theta \sin \theta_{2}|v|$
       $=\sin \theta \sin \theta_{2}|v||k|$
       $=\sin \theta |k \times v|$
由公式 $|a\times b| = \sin \theta |a||b|$知 $\sin \theta_{2}|v||k|=|k\times v|$，所以：
$|a|=\sin \theta |k \times v|$

方向
由叉乘方向可得 $a$的单位方向向量为： $k\times v /|k \times v|$，综上可得：
$a=(k\times v /|k \times v|)|a|$
     $=(k\times v /|k \times v|)\sin \theta |k \times v|$
     $=\sin \theta k\times v$

2.2.4 推导 $b$

大小
由图得， $\theta_{1}$为 $b$和 $v_{rot\perp }$的夹角，则：
$|b|=\cos \theta_{1}|v_{rot\perp }|=\cos (\pi -\theta)|v_{\perp }|= -\cos \theta|v_{\perp }|$

方向
由于 $b$的方向与 $v_{\perp }$方向相反，可得 $b$的单位方向向量为： $-v_{\perp }/|v_{\perp }|$，综上可得：
$b=(-v_{\perp }/|v_{\perp }|)|b|$
     $=\cos \theta v_{\perp }$

至此，罗德里格斯公式的证明全部结束。此外，如果读者希望获得关于Oxyz坐标系的旋转变换关系，可以参考这篇博客：图形变换之旋转变换公式推导。
罗德里格斯公式反应的是旋转向量到旋转矩阵的转换关系，如果已知旋转矩阵 $R$，如果推导旋转向量 $v$呢？下边给出旋转矩阵到旋转向量的反向转换关系。

3.旋转矩阵到向量

这里计算从一个旋转矩阵到旋转向量的转换。对于旋转角 $\theta$，取旋转矩阵 $R$两边的迹，有： $\begin{aligned} tr(R) &= \cos \theta tr(I)+(1-\cos \theta )tr(nn^{T})+\sin \theta tr(n^{\wedge })\\ &=3\cos \theta + (1- \cos \theta) \\ &=1+2\cos \theta. \tag{1.4} \end{aligned}$因此： $\theta = \arccos \frac{tr(R)-1}{2} .\tag{1.5}$关于转轴 $n$，旋转轴上的向量在旋转后不发生改变，说明： $Rn=n.\tag{1.6}$因此，转轴 $n$是矩阵 $R$特征值1对应的特征向量。求解此方程，再归一化，就得到了旋转轴 $n$。由 $v=\theta n$得到旋转向量 $v$。

至此，推导结束。实践部分代码放到第三部分一起演示。

参考：
1.《视觉SLAM十四讲：从理论到实践》，高翔、张涛等著，中国工信出版社
2. 罗德里格斯公式推导