目录
上接(第二章:神经网络编程的基础知识)
第三章:实现一个神经网络
- 3.1神经网络概览
- 3.2神经网络表示
- 3.3计算神经网络的输出
- 3.4多个样本的向量化
- 3.5向量化实现的解释
- 3.6激活函数
- 3.7为什么需要非线性激活函数?
- 3.8激活函数的导数
- 3.9神经网络的梯度下降算法的具体实现
- 3.10(选修)直观理解反向传播(略)
- 3.11随机初始化
对应的编程代码实现
3.1神经网络概览

统一规定:【】表示神经网络层;()表示单个训练样本的相关标识
Eg.a[0]_1表示输入层的第一个向量x1
3.2神经网络表示
先看只有一个隐藏层的神经网络(单隐藏神经网络):

神经网络的输入层:输入特征x1、x2、x3的竖向堆叠,有时也可见到a【0】=x的表现形式(a—activations),即输入存于输入层a【0】中;
神经网络的隐藏层:与输入紧连的圆圈层;其含义为:在训练集中,这些中间结点的真正数值用户并不可见,通过z=w^Tx+b,α= sigmoid(z)产生的激活值存于a【1】中
神经网络的输出层:隐藏层汇聚的唯一节点所在的层,按照权重求取平均负责输出预测的y值

上述在约定俗成中往往被称为“双层神经网络”,这是因为人们不把输入层看作一个标准的层。
3.3计算神经网络的输出

圆圈:表示回归计算的两个步骤(①先计算z②再代入sigmoid函数)

故我们可以发现:
Z[1]=W^[1]*X+b[1]
a[1]=sigmoid(Z^[1])
//注意:W^[1]=W的一次转置(W^T);a【1】也是一个4*1的列向量
//再代入输出层a【2】中有相同的回归运算:
Z[2]=W^[2]*a[1]+b[2]
a[2]=sigmoid(Z^[2])
//注:W^[2]=W的两次转置(即为w本身)a【1】成为相较于a【2】的“输入层”
3.4多个样本的向量化
用[ ]与()的结合,将向量数据用矩阵表示,下标不同的对应神经网络中不同的节点。
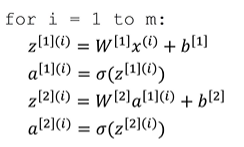
注:x=a【0】;x(i)=a【0】(i)
3.5向量化实现的解释

3.6激活函数

3.6.1 sigmoid函数
x是输入量,w是权重,b是偏移量(bias);上述使用的sigmoid函数只是激活函数中的一种,主要用于二元分类的输出层。
3.6.2 g(z)=tanh(z)(双曲正切函数)


观察图像可得tanh实际上是Sigmoid平移缩放后的版本:

tanh(x)=2σ(2x)−1
它让signoid的零点与坐标轴原点(0,0)对齐,使其值域在(-1,1);这样就使得tanh函数输出介于-1和1之间,激活函数的平均值就更接近于0(而不是像sigmoid的0.5)以达到数据中心化与方便下一层神经网络学习的效果。
当然在面临二元分类问题时(即预想输出应该是介于0-1之间的概率),sigmoid因为其值域正好是(0,1)而优于tanh。所以借用3.2中的单隐藏神经络为例,我们可以在隐藏层中的激活函数使用tanh,在输出层中的激活函数使用sigmoid。
如果当输入值x非常大或者非常小时(往往出现在神经网络层数增多,链式求导,多项相乘,函数饱和等情况),斜率变化非常缓慢导致梯度很小接近于0,这样会拖慢梯度下降算法:

于是需要我们使用到所谓的修正线性单元(ReLU)
3.6.3ReLU函数
①默认的ReLU函数:

简化公式就是a=max(0,z)
ReLU是神经网络中常用的激活函数。ReLU的输入是x,当x>0, 其梯度=1, 可用于权重更新;当x<0, 其梯度为0, 权重无法更新,后续训练中处于静默状态(神经元处于不学习状态)。
实际运用中很多z空间激活函数的导数都和0差的很远,所以使用ReLU激活函数可以避免因为函数斜率接近0而带来的学习速度减慢的效应,从而会比tanh与sigmoid快得多.
②带泄露的ReLU函数


Leaky Relu:(与Relu的不同之处在于负轴保留了非常小的常数leak,使得输入信息小于0时,信息没有完全丢掉,进行了相应的保留),即ReLU在取值小于零部分梯度为0,而LeakyReLU在取值小于0部分给一个很小的梯度其值为leak(视频中给出的示例为a=max(0.01z,z)其对应的leak=0.01)
3.7为什么需要非线性激活函数?
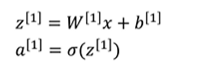
在最开始规范输出值y的时候,会有疑问,为什么不直接让a=z(或者与之类似的恒等线性激活函数)?这是因为:
原因1:
如果不用非线性的激励函数,每一层输出都是上层输入的线性组合,无论神经网络有多少层,输出都是输入的线性组合。
例如我们可以假设:
a[1]=z[1]=w[1]x+b[1]
a[2]=z[2]=w[2]a[1]+b[2]
=w[2]( w[1]x+b[1]) +b[2]
=w[2]w[1]x+w[2]b[1] +b[2]
此时令w0=w[2]w[1]
b0=w[2]b[1] +b[2]
a[2]=w0*x + b0
可见隐藏层的分层的优越性就无法体现,甚至全部去掉都对最后的结果没有影响。
原因2:

在单层感知机中,分类的结果大于某个值为一类,小于某个值为一类,这样的话就会使得输出结果在这个点发生阶跃,而往往这个阶跃不符合神经元的逻辑规律,所以给激活函数引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中

比如上图的logistic函数(sigmoid)就解决了阶跃函数的突然阶跃问题,使得输出的为0-1的概率,使得结果变得更平滑,他是一个单调上升的函数,具有良好的连续性,不存在不连续点
3.8激活函数的导数
①sigmoid函数:

x是输入量,w是权重,b是偏移量(bias)
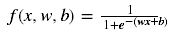
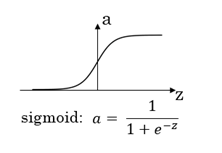
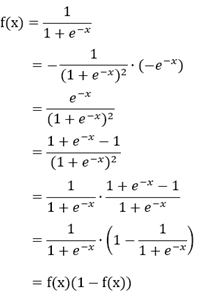
②tanh函数:

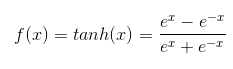
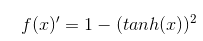
当 x = 10, 或 x = -10 时,f(x)‘≈0;当 x = 0 时, f(x)’=1
求导过程如下:
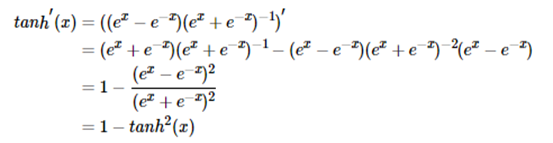
③ReLU函数:

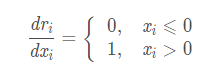
3.9神经网络的梯度下降算法的具体实现
神经网络中的正向传播过程:
Z[1]=W^[1]*X+b[1]
a[1]=g[1](Z^[1])
Z[2]=W^[2]*a[1]+b[2]
a[2]=g[2](Z^[2])=sigmoid(Z^[2])
神经网络的反向传播过程:(Y是1*m矩阵,它将m个样本横向堆叠)
"dz[2]"=A[2]-Y//证明详见2.9
"dw[2]"=1/m *"dz[2]"*(A[1]^T)
"db[2]"=1/m*np.sum("dz[2]",axis=1,keepdims=True)
//keepdims是防止python直接输出秩为1的数组
"dz[1]"=(w[2]^T)*"dz[2]"*g[1]'(z[1])
// g[1]'(z[1])是隐藏层的激活函数对应的导数
"dw[1]"=1/m *"dz[1]"*(x^T)
"db[1]"=1/m*np.sum("dz[1]",axis=1,keepdims=True)
3.11随机初始化
对于logistic回归,可以将权重w初始化为0,但如果将神经网络的各个参数数组全部初始化为0,再使用梯度下降算法,那会完全无效,示例如下:
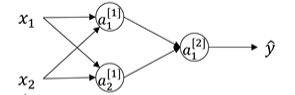
我们拥有两个输入特征,所以n^[0]=2;有两个隐藏单元,所以n^[1]=2;所以和隐藏层有关的矩阵w应该为2*2,这样一来就会导致初始化时,两个隐藏单元在做同样的计算,两个隐藏单元对输出单元的影响也一样大,再一次迭代之后,同样的对称性依然存在,在这样的情况下,多个隐藏单元将没有意义。因此对于权重w的初始化我们改为:
W^[1]=np.random.randn((2,2))
//这样就可以产生参数为(2,2)的高斯分布随机变量
W^[1]= W^[1]*0.01
//再乘以一个很小的数字,便可以将权重初始化成很小的随机数
而b[1]则不用考虑w的重复破坏性问题,因为经过不同w的函数运算,b不具有完全对称性;所以b[1]可以初始化为0
同理,对w[2]和b[2]进行相同的初始化