吴恩达 deeplearning.ai 专项课程第一课
基于coursera的honor code,代码将不会直接贴出来,
本次作业你将会学到:
本节目的:理解np.exp() 优于 math.exp().
作业 :
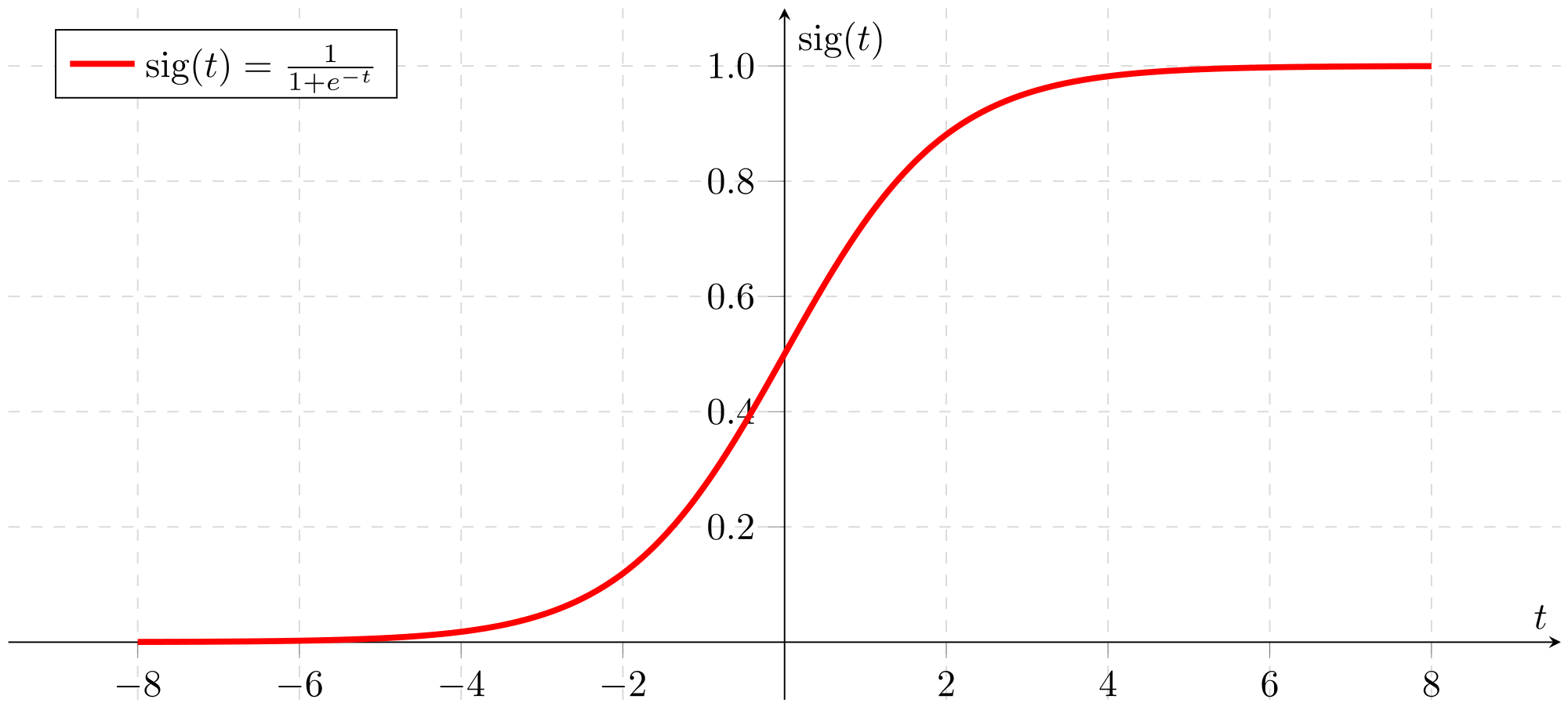
练习:建立一个能够返回实数X的sigmoid,使用maath.exp(x)
s
i
g
m
o
i
d
(
x
)
=
1
1
+
e
−
x
sigmoid(x) = \frac{1}{1+e^{-x}}
s i g m o i d ( x ) = 1 + e − x 1
如果你将一个矩阵输入math.exp(x)函数中,会报错One reason why we use “numpy” instead of “math” in Deep Learning
事实上,如果
x
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
x = (x_1, x_2, ..., x_n)
x = ( x 1 , x 2 , . . . , x n )
n
p
.
e
x
p
(
x
)
np.exp(x)
n p . e x p ( x )
n
p
.
e
x
p
(
x
)
=
(
e
x
1
,
e
x
2
,
.
.
.
,
e
x
n
)
np.exp(x) = (e^{x_1}, e^{x_2}, ..., e^{x_n})
n p . e x p ( x ) = ( e x 1 , e x 2 , . . . , e x n )
作业 :
将1.1中写的sigmoid函数赋给s.
计算
σ
′
(
x
)
=
s
(
1
−
s
)
\sigma'(x) = s(1-s)
σ ′ ( x ) = s ( 1 − s ) 注意 :本处也需要用)sigmoid求导为何等于a(1-a)的形式?详见激活函数求导证明
使用函数:关于numpy的多项式及求导,详见Numpy 多项式函数、求导
np.shape and np.reshape()函数
X.shape 得到X的维度
X.reshape(…) 用于将X变成其它维度的矩阵
①np.reshape()函数官方介绍(英文)
a:待处理的矩阵
newshape:新的矩阵的格式,使用int或tuple of ints表示
order:取值范围{‘C’, ‘F’, ‘A’} 默认为C
#原始矩阵
[0, 1],
[2, 3],
[4, 5]
# C :
[0, 1, 2],
[3, 4, 5]
# F:
[0, 4, 3],
[2, 1, 5]
# A:
[0, 2, 4],
[1, 3, 5]
行归一化 令
x
x
x
x
∥
x
∥
\frac{x}{\| x\|}
∥ x ∥ x
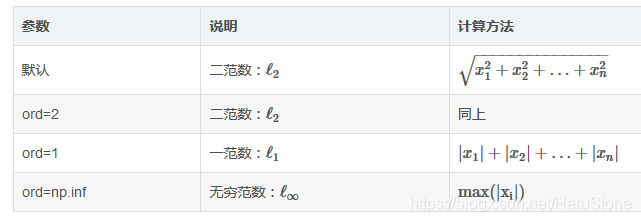
np.linalg.norm(x, ord=None, axis=None, keepdims=False)函数
ord 设置具体范数值
axis 向量的计算方向
keepdims 设置是否保持维度不变
for
x
∈
R
1
×
n
,
s
o
f
t
m
a
x
(
x
)
=
s
o
f
t
m
a
x
(
[
x
1
x
2
.
.
.
x
n
]
)
=
[
e
x
1
∑
j
e
x
j
e
x
2
∑
j
e
x
j
.
.
.
e
x
n
∑
j
e
x
j
]
\text{for } x \in \mathbb{R}^{1\times n} \text{, } softmax(x) = softmax(\begin{bmatrix} x_1 &&x_2 && ... && x_n \end{bmatrix}) = \begin{bmatrix} \frac{e^{x_1}}{\sum_{j}e^{x_j}} && \frac{e^{x_2}}{\sum_{j}e^{x_j}} && ... && \frac{e^{x_n}}{\sum_{j}e^{x_j}} \end{bmatrix}
for x ∈ R 1 × n , s o f t m a x ( x ) = s o f t m a x ( [ x 1 x 2 . . . x n ] ) = [ ∑ j e x j e x 1 ∑ j e x j e x 2 . . . ∑ j e x j e x n ]
x
∈
R
m
×
n
,
x
i
j
为第
i
t
h
行和
j
t
h
列
\text{} x \in \mathbb{R}^{m \times n} \text{, $x_{ij}$ 为第 $i^{th}$行和$j^{th}$ 列}
x ∈ R m × n , x i j 为第 i t h 行和 j t h 列
s
o
f
t
m
a
x
(
x
)
=
s
o
f
t
m
a
x
[
x
11
x
12
x
13
…
x
1
n
x
21
x
22
x
23
…
x
2
n
⋮
⋮
⋮
⋱
⋮
x
m
1
x
m
2
x
m
3
…
x
m
n
]
=
[
e
x
11
∑
j
e
x
1
j
e
x
12
∑
j
e
x
1
j
e
x
13
∑
j
e
x
1
j
…
e
x
1
n
∑
j
e
x
1
j
e
x
21
∑
j
e
x
2
j
e
x
22
∑
j
e
x
2
j
e
x
23
∑
j
e
x
2
j
…
e
x
2
n
∑
j
e
x
2
j
⋮
⋮
⋮
⋱
⋮
e
x
m
1
∑
j
e
x
m
j
e
x
m
2
∑
j
e
x
m
j
e
x
m
3
∑
j
e
x
m
j
…
e
x
m
n
∑
j
e
x
m
j
]
=
(
s
o
f
t
m
a
x
(first row of x)
s
o
f
t
m
a
x
(second row of x)
.
.
.
s
o
f
t
m
a
x
(last row of x)
)
softmax(x) = softmax\begin{bmatrix} x_{11} & x_{12} & x_{13} & \dots & x_{1n} \\ x_{21} & x_{22} & x_{23} & \dots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & x_{m3} & \dots & x_{mn} \end{bmatrix} = \begin{bmatrix} \frac{e^{x_{11}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{12}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{13}}}{\sum_{j}e^{x_{1j}}} & \dots & \frac{e^{x_{1n}}}{\sum_{j}e^{x_{1j}}} \\ \frac{e^{x_{21}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{22}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{23}}}{\sum_{j}e^{x_{2j}}} & \dots & \frac{e^{x_{2n}}}{\sum_{j}e^{x_{2j}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{e^{x_{m1}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m2}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m3}}}{\sum_{j}e^{x_{mj}}} & \dots & \frac{e^{x_{mn}}}{\sum_{j}e^{x_{mj}}} \end{bmatrix} = \begin{pmatrix} softmax\text{(first row of x)} \\ softmax\text{(second row of x)} \\ ... \\ softmax\text{(last row of x)} \\ \end{pmatrix}
s o f t m a x ( x ) = s o f t m a x ⎣ ⎢ ⎢ ⎢ ⎡ x 1 1 x 2 1 ⋮ x m 1 x 1 2 x 2 2 ⋮ x m 2 x 1 3 x 2 3 ⋮ x m 3 … … ⋱ … x 1 n x 2 n ⋮ x m n ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∑ j e x 1 j e x 1 1 ∑ j e x 2 j e x 2 1 ⋮ ∑ j e x m j e x m 1 ∑ j e x 1 j e x 1 2 ∑ j e x 2 j e x 2 2 ⋮ ∑ j e x m j e x m 2 ∑ j e x 1 j e x 1 3 ∑ j e x 2 j e x 2 3 ⋮ ∑ j e x m j e x m 3 … … ⋱ … ∑ j e x 1 j e x 1 n ∑ j e x 2 j e x 2 n ⋮ ∑ j e x m j e x m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎝ ⎜ ⎜ ⎛ s o f t m a x (first row of x) s o f t m a x (second row of x) . . . s o f t m a x (last row of x) ⎠ ⎟ ⎟ ⎞