Deeplearning.ai吴恩达笔记之神经网络和深度学习2

Logistic Regression as a Neural Network

Binary Classification

在这里插入图片描述

如上图所示，这是一个典型的二分类问题。一般来说，彩色图片包含RGB三个通道。例如该cat图片的尺寸为（64，64，3）。在神经网络模型中，我们首先要将图片输入x（维度是（64，64，3））转化为一维的特征向量（feature vector）。方法是每个通道一行一行取，再连接起来。由于64x64x3=12288，则转化后的输入特征向量维度为（12288，1）。

Logistic Regression

在这里插入图片描述

Logistic Regression Cost Function

在这里插入图片描述

如何定义所有m个样本的cost function呢？先从单个样本出发，我们希望该样本的预测值ŷ y^与真实值越相似越好。我们把单个样本的cost function用Loss function来表示，根据以往经验，可以使用平方错误（squared error）来衡量，如下所示：

$L(ŷ ,y)=\frac{1}{2}(ŷ −y)^2$

但是，对于逻辑回归，我们一般不使用平方错误来作为Loss function。原因是这种Loss function一般是non-convex的。non-convex函数在使用梯度下降算法时，容易得到局部最小值（local minumum），即局部最优化。而我们最优化的目标是计算得到全局最优化（Global optimization）。因此，我们一般选择的Loss function应该是convex的，则：

$L(ŷ ,y)=−(ylog ŷ +(1−y)log (1−ŷ ))$

还要提一点的是，上面介绍的Loss function是针对单个样本的。那对于m个样本，我们定义Cost function，Cost function是m个样本的Loss function的平均值，反映了m个样本的预测输出ŷ y^与真实样本输出y的平均接近程度。Cost function可表示为： $J(w,b)=\frac{1}{m}\sum_{i=1}^mL(ŷ^{(i)},y^{(i)})=−\frac{1}{m}\sum_{i=1}^m[y^{(i)}log ŷ^{(i)}+(1−y^{(i)})log (1−ŷ^{(i)})]$

Gradient Descent

由于J(w,b)是convex function，梯度下降算法是先随机选择一组参数w和b值，然后每次迭代的过程中分别沿着w和b的梯度（偏导数）的反方向前进一小步，不断修正w和b。每次迭代更新w和b后，都能让J(w,b)更接近全局最小值。梯度下降的过程如下图所示。

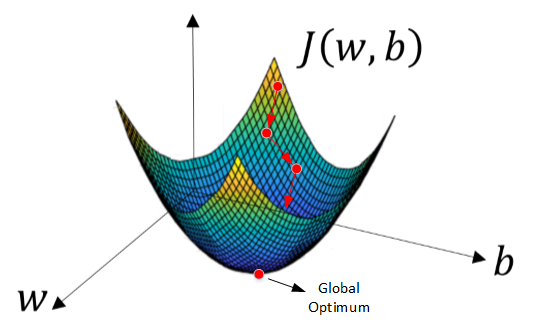
在这里插入图片描述

梯度下降算法每次迭代更新，w和b的修正表达式为：

$w:=w−α\frac{∂J(w,b)}{∂w}$

$b:=b−α\frac{∂J(w,b)}{∂b}$

上式中， $\alpha$ 是学习因子（learning rate），表示梯度下降的步进长度。 $\alpha$ 越大，w和b每次更新的“步伐”更大一些； $\alpha$ 越小，w和b每次更新的“步伐”更小一些。

Derivatives

略

More Derivative Examples

略

Computation graph

整个神经网络的训练过程实际上包含了两个过程：正向传播（Forward Propagation）和反向传播（Back Propagation）。正向传播是从输入到输出，由神经网络计算得到预测输出的过程；反向传播是从输出到输入，对参数w和b计算梯度的过程。下面，我们用计算图（Computation graph）的形式来理解这两个过程。

举个简单的例子，假如Cost function为J(a,b,c)=3(a+bc)，包含a，b，c三个变量。我们用u表示bc，v表示a+u，则J=3v。它的计算图可以写成如下图所示：

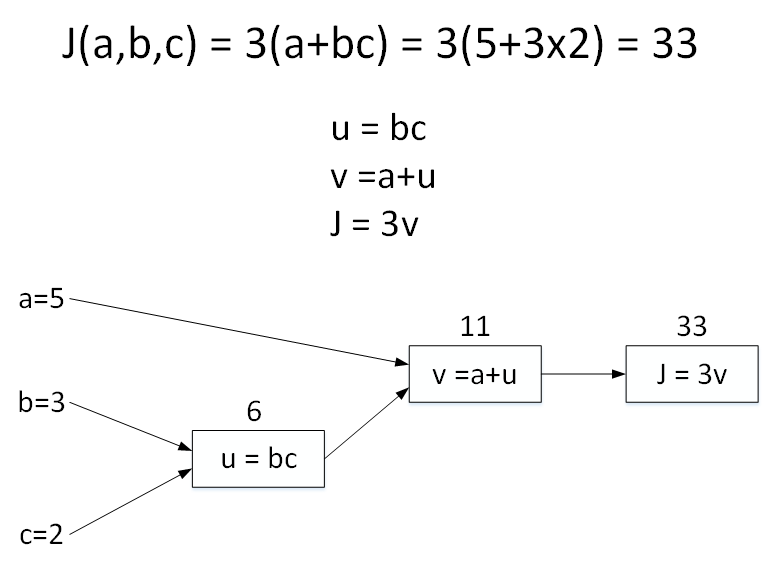
在这里插入图片描述

令a=5，b=3，c=2，则u=bc=6，v=a+u=11，J=3v=33。计算图中，这种从左到右，从输入到输出的过程就对应着神经网络或者逻辑回归中输入与权重经过运算计算得到Cost function的正向过程。

###Derivatives with a Computation Graph

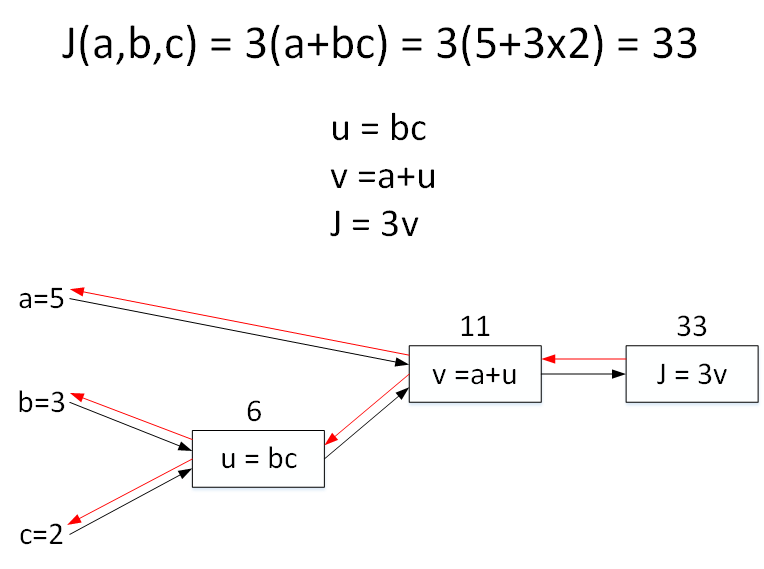
在这里插入图片描述

首先计算J对参数a的偏导数。从计算图上来看，从右到左，J是v的函数，v是a的函数。则利用求导技巧，可以得到：

			$\frac{∂J}{∂a}=\frac{∂J}{∂v}⋅\frac{∂v}{∂a}=3⋅1=3$

根据这种思想，然后计算J对参数b的偏导数。从计算图上来看，从右到左，J是v的函数，v是u的函数，u是b的函数。可以推导：

$\frac{∂J}{∂b}=\frac{∂J}{∂v}⋅\frac{∂v}{∂u}⋅\frac{∂u}{∂b}=3⋅1⋅c=3⋅1⋅2=6$
最后计算J对参数c的偏导数。仍从计算图上来看，从右到左，J是v的函数，v是u的函数，u是c的函数。可以推导：

$\frac{∂J}{∂c}=\frac{∂J}{∂v}⋅\frac{∂v}{∂u}⋅\frac{∂u}{∂c}=3⋅1⋅b=3⋅1⋅3=9$
为了统一格式，在程序代码中，我们使用da，db，dc来表示J对参数a，b，c的偏导数。

Logistic Regression Gradient Descent

现在，我们将对逻辑回归进行梯度计算。对单个样本而言，逻辑回归Loss function表达式如下：

$z=w^Tx+b$
$ŷ =a=σ(z)$
$L(a,y)=−(ylog(a)+(1−y)log(1−a))$
首先，该逻辑回归的正向传播过程非常简单。根据上述公式，例如输入样本x有两个特征(x1,x2)，相应的权重w维度也是2，即(w1,w2)。则 $z=w_1x_1+w_2x_2+b$ ，最后的Loss function如下所示：

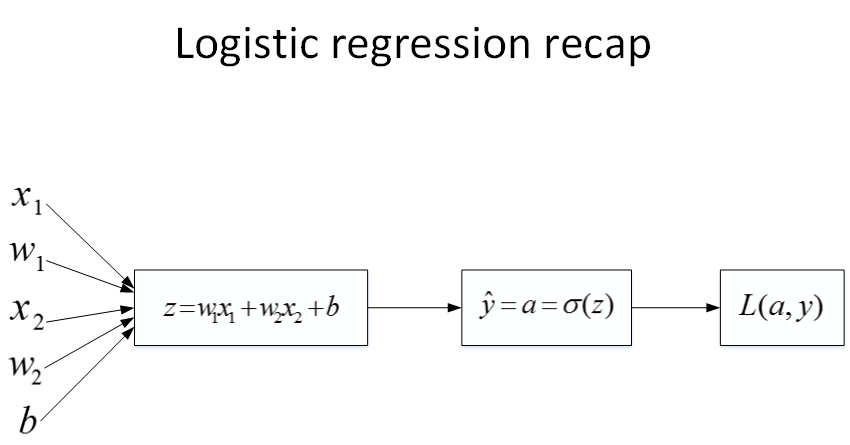
在这里插入图片描述

然后，计算该逻辑回归的反向传播过程，即由Loss function计算参数w和b的偏导数。推导过程如下：

$da=\frac{∂L}{∂a}=−\frac{y}{a}+\frac{1−y}{1−a}$
$dz=\frac{∂L}{∂z}=\frac{∂L}{∂a}⋅\frac{∂a}{∂z}=(−\frac{y}{a}+\frac{1−y}{1−a})⋅a{(1−a)}=a−y$
知道了dz之后，就可以直接对 $w_1$ ， $w_2$ 和b进行求导了。
$dw_1=\frac{∂L}{∂w_1}=\frac{∂L}{∂z}⋅\frac{∂z}{∂w_1}=x_1⋅dz=x1(a−y)$
$dw_2=\frac{∂L}{∂w_2}=\frac{∂L}{∂z}⋅\frac{∂z}{∂w_2}=x2⋅dz=x_2(a−y)$
$db=\frac{∂L}{∂b}=\frac{∂L}{∂z}⋅\frac{∂z}{∂b}=1⋅dz=a−y$
则梯度下降算法可表示为：
$w_1:=w_1−α dw_1$
$w_2:=w_2−α dw_2$
$b:=b−α db$
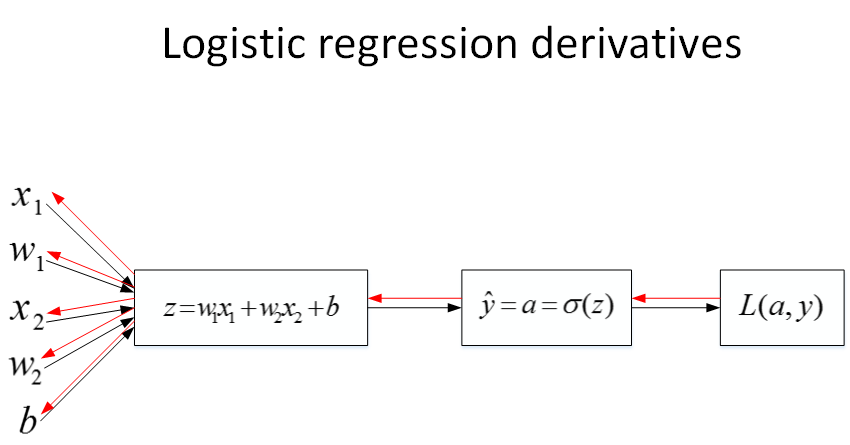
在这里插入图片描述

Gradient descent on m examples

在这里插入图片描述

Summary

本节课的内容比较简单，主要介绍了神经网络的基础——逻辑回归。首先，我们介绍了二分类问题，以图片为例，将多维输入x转化为feature vector，输出y只有{0,1}两个离散值。接着，我们介绍了逻辑回归及其对应的Cost function形式。然后，我们介绍了梯度下降算法，并使用计算图的方式来讲述神经网络的正向传播和反向传播两个过程。最后，我们在逻辑回归中使用梯度下降算法，总结出最优化参数w和b的算法流程。

Python and Vectorization

Vectorization

深度学习算法中，使用向量化矩阵运算的效率要高得多。

为了加快深度学习神经网络运算速度，可以使用比CPU运算能力更强大的GPU。事实上，GPU和CPU都有并行指令（parallelization instructions），称为Single Instruction Multiple Data（SIMD）。SIMD是单指令多数据流，能够复制多个操作数，并把它们打包在大型寄存器的一组指令集。SIMD能够大大提高程序运行速度，例如python的numpy库中的内建函数（built-in function）就是使用了SIMD指令。相比而言，GPU的SIMD要比CPU更强大一些。

More Vectorization Examples

上一部分我们讲了应该尽量避免使用for循环而使用向量化矩阵运算。在python的numpy库中，我们通常使用np.dot()函数来进行矩阵运算。

我们将向量化的思想使用在逻辑回归算法上，尽可能减少for循环，而只使用矩阵运算。值得注意的是，算法最顶层的迭代训练的for循环是不能替换的。而每次迭代过程对J，dw，b的计算是可以直接使用矩阵运算。

Vectorizing Logistic Regression

利用向量化的思想，所有m个样本的线性输出Z可以用矩阵表示：
$Z=w^TX+b$
在python的numpy库中可以表示为：

Z = np.dot(w.T,X) + b
A = sigmoid(Z)

其中，w.T表示w的转置。

这样，我们就能够使用向量化矩阵运算代替for循环，对所有m个样本同时运算，大大提高了运算速度。

###Vectorizing Logistic Regression’s Gradient Output

在这里插入图片描述

Broadcasting in Python

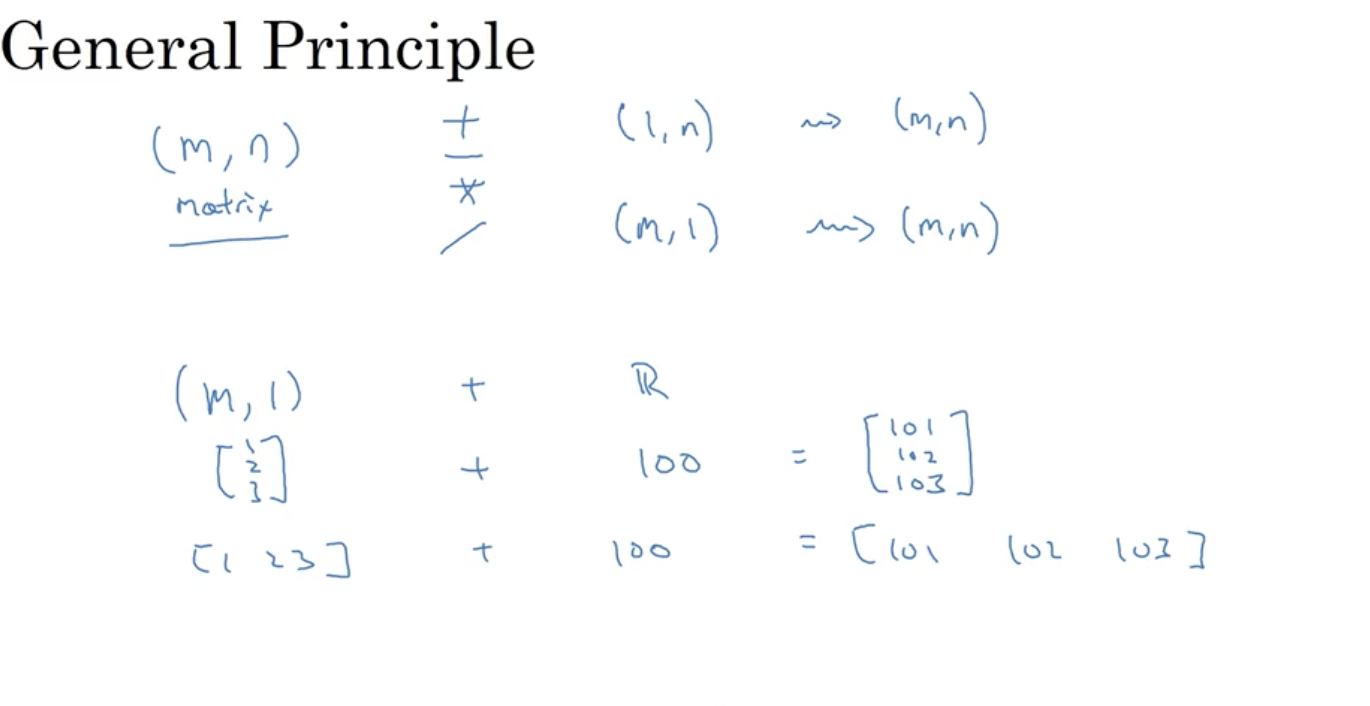
在这里插入图片描述

A note on python/numpy vectors

接下来我们将总结一些python的小技巧，避免不必要的code bug。
python中，如果我们用下列语句来定义一个向量：

a = np.random.randn(5)

这条语句生成的a的维度是（5，）。它既不是行向量也不是列向量，我们把a叫做rank 1 array。这种定义会带来一些问题。例如我们对a进行转置，还是会得到a本身。所以，如果我们要定义（5，1）的列向量或者（1，5）的行向量，最好使用下来标准语句，避免使用rank 1 array。

a = np.random.randn(5,1)
b = np.random.randn(1,5)

除此之外，我们还可以使用assert语句对向量或数组的维度进行判断，例如：

assert(a.shape == (5,1))
assert会对内嵌语句进行判断，即判断a的维度是不是（5，1）的。如果不是，则程序在此处停止。使用assert语句也是一种很好的习惯，能够帮助我们及时检查、发现语句是否正确。

另外，还可以使用reshape函数对数组设定所需的维度：

a.reshape((5,1))

Explanation of logistic regression cost function

在上一节课的笔记中，我们介绍过逻辑回归的Cost function。接下来我们将简要解释这个Cost function是怎么来的。
首先，预测输出ŷ的表达式可以写成：
$ŷ =σ(w^Tx+b)$
其中， $σ(z)=\frac{1}{1+exp(−z)}$ 。ŷ 可以看成是预测输出为正类（+1）的概率：
$ŷ =P(y=1|x)$
那么，当y=1时：
$p(y|x)=ŷ$
当y=0时：
$p(y|x)=1−ŷ $
我们把上面两个式子整合到一个式子中，得到：
$P(y|x)=ŷ^y(1−ŷ )^(1−y)$
由于log函数的单调性，可以对上式P(y|x)进行log处理：
$log\ P(y|x)=log ŷ^y(1−ŷ )^{(1−y)}=ylog ŷ+(1−y)log(1−ŷ)$
我们希望上述概率P(y|x)越大越好，对上式加上负号，则转化成了单个样本的Loss function，越小越好，也就得到了我们之前介绍的逻辑回归的Loss function形式。
$L=−(ylog ŷ +(1−y)log(1−ŷ))$
如果对于所有m个训练样本，假设样本之间是独立同分布的（iid），我们希望总的概率越大越好：
$max \prod_{i=1}^m P(y(i)|x(i))$
同样引入log函数，加上负号，将上式转化为Cost function:
$J(w,b)=−\frac{1}{m}\sum_{i=1}^mL(ŷ^{(i)},y^{(i)})=−\frac{1}{m}\sum_{i=1}^my^{(i)}log ŷ^{(i)}+(1−y^{(i)})log(1−ŷ^{(i)})$
上式中， $\frac{1}{m}$ 表示对所有m个样本的Cost function求平均，是缩放因子。

Summary

本节课我们主要介绍了神经网络基础——python和向量化。在深度学习程序中，使用向量化和矩阵运算的方法能够大大提高运行速度，节省时间。以逻辑回归为例，我们将其算法流程包括梯度下降转换为向量化的形式。同时，我们也介绍了python的相关编程方法和技巧。