降维
机器学习的算法的计算量往往伴随着维度\(d\)的增长呈现指数型增长,例如线性感知机的VC维是\(d+1\)
去除无用的维度,保留有用的特征可以减少计算量同时提高精度
\(\mathtt{z=\Phi(x)}\),\(\mathtt{x}\)为原始输入向量,\(\mathtt{z}\)为变换后输入向量
假如\(\mathtt{z}\)的维度小于\(\mathtt{x}\)的维度,那么就实现了降维
理想的输入向量维度应该和目标函数输入的维度保持一致,这说明特征选择和辨识目标函数一般难
在非线性特征转换中我们增加维度来努力提高样本内误差,付出的代价是降低了泛化能力,相反来说,如果我们可以在不损伤样本内误差的情况下降低维度,那我们就可以提高泛化能力.
PCA(主成分分析)
PCA构造少量的线性特征来总结输入数据,想法就是旋转坐标轴(一种线性转换定义一个新的坐标系统),在这个新的坐标系统中重要的维度变得明显,可以被保留而不重要的维度可以舍弃.

旋转后的数据\(z_1\)轴更为重要,\(z_2\)轴显得没那么重要,看起来就像是一系列小的波动(噪音),我们可以忽略它(设置其为零),这样就实现了降维
在二维数据中我们可以使用一个向量\(\mathtt{v}\)来捕获这个方向的最大波动
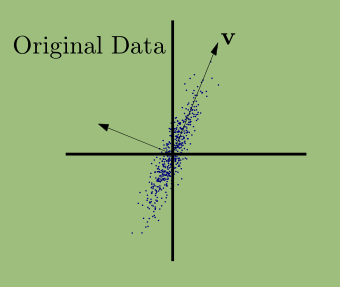
数据点在\(\mathtt{v}\)这个方向的投影\(z_n\)可以反映一个数据点在\(\mathtt{v}\)方向的波动,而整体的波动可以用方差衡量(假设数据已经定心)
\(z_n=\mathtt{v^Tx}\)
\(\mathtt{C}\)是指协方差矩阵
\(\begin{equation} \begin{split} var[z]=\frac{1}{N}\sum_{n=1}^Nz_n^2&=\frac{1}{N}\mathtt{v^Tx_nx_n^Tv}\\ &=\mathtt{v^T}(\frac{1}{N}\mathtt{x_nx_n^T})\mathtt{v}\\ &=\mathtt{v^TCv} \end{split} \end{equation}\)
为了最大化数据点在\(\mathtt{v}\)方向的波动,我们应该最大化方差,因此我们只要选取\(\mathtt{v}\)作为协方差矩阵的最大特征值的特征向量.
降维后数据
\(\mathtt{X'=Xv^T}\)
\(\mathtt{Ax=\lambda x}\),A是方矩阵,\(\mathtt{x}\)是列向量,\(\lambda\)是数,如果前式成立那么就称\(\lambda\)是方矩阵对应于列向量\(\mathtt{x}\)的特征值,特征向量可以通过解\(|\lambda E-\mathtt{A}|\)来得出
运用线性代数的几何意义,矩阵就是将一个向量变为另一个向量的变换,在\(var[z]=\mathtt{v^TCv}\)中,\(\mathtt{Cv}\)的几何意义就是将向量\(\mathtt{v}\)进行变换,\(\mathtt{v^TCv}\)的几何意义就是将变换后的向量再投影到原向量上..
为了最大化\(var[z]\),变换后的向量投影要最大,显而易见同一方向的两个向量投影大,要是变换后向量不仅同向,而且放大了一定倍数就更好了,这完全符合矩阵的大特征值的特征向量的概念
一个方矩阵的特征向量是指这个方矩阵的变换作用在特征向量上,并不会发生旋转,只发生伸缩变换(即方向不变).而特征值正好反应这个缩放的程度,绝对值大于1是放大,绝对值小于1大于0是缩小,负号是反向,正号是正向.
我们选取其中特征值较大的k个特征向量组成V,\(\mathtt{V}=\begin{bmatrix}{\mathtt{v_1}}&{\mathtt{v_2}}&{\cdots}&{\mathtt{v_k}}\end{bmatrix},\mathtt{V}\in R^{d*k}\)
\(\mathtt{X}\in R^{N*d}\)
最终转换后的输入数据\(\mathtt{X'=XV}\),这样就将维度从d降到了k
如果不懂线性代数的物理意义请去看线性代数的本质
顺带一说白化使得各个方向都是相等的,所以在白化后做PCA是没有用的
坐标系统
一个坐标系统由标准坐标基(一系列互相正交的单位向量\(\mathtt{v_1,...,v_d}\))坐标确定
自然基\(\mathtt{u_1,...,u_i}\)是指单位向量\(\mathtt{u_i}\)第i个元素为1,其余为0
自然基确定的空间中的向量\(\mathtt{x}\)在标准正交基\(\mathtt{v_1,...,v_d}\)确定的空间中的坐标为\(\mathtt{x'=\sum_{i=1}^dz_iv_i=\sum_{i=1}^d(x^Tv_i)v_i}\)
\(z_i\)描述了\(\mathtt{x}\)在\(\mathtt{v_i}\)基上的分量(投影)
\(\mathtt{z}=\begin{bmatrix}z_1\\\vdots\\z_k\end{bmatrix}=\begin{bmatrix}\mathtt{x^Tv_i}\\\vdots\\\mathtt{x^Tv_k}\end{bmatrix}=\Phi(x)\)
如果我们标准正交基\(\mathtt{v_1,...,v_d}\)的数量和输入特征一致,那么我们可以重构\(\mathtt{x}\)通过
\(\mathtt{x=\sum_{i=1}^dz_iv_i}\)
如果只保留前k个部分
\(\mathtt{\hat{x}=\sum_{i=1}^dz_iv_i}\)
我们丢失了部分分量实现了降维
一个数据点重构后丢失的部分可以通过下面误差衡量
\(||\mathtt{x-\hat{x}}||^2=||\sum_{i=k+1}^dz_i\mathtt{v}_i||^2=\sum_{i=k+1}^dz_i^2\)
由于\(\mathtt{v_i}\)是单位向量长度为1
所有数据点重构后丢失的部分可以通过以下误差衡量
\(\sum_{n=1}^N||\mathtt{x-\hat{x}}||^2\)
主成分分析(PCA)找到一个坐标系统,使总重构误差最小化。尾随维度将包含尽可能少的信息,因此即使丢弃了这些尾随维度,我们仍然几乎可以重构原始数据。PCA是最优的,这意味着没有其他线性方法可以生成重构误差较小的坐标。这个最优坐标基中前k个基向量,叫做top-k主方向。
SVD(奇异值分解)
通过奇异值分解得到右奇异向量,以此作为\(\mathtt{v_1,...,v_d}\)(最优坐标基),然后忽略尾随分量来减少重构误差
任意一个矩阵\(\mathtt X\)都可以分解为以下形式
\(\mathtt{X=U\Gamma V^T}\)
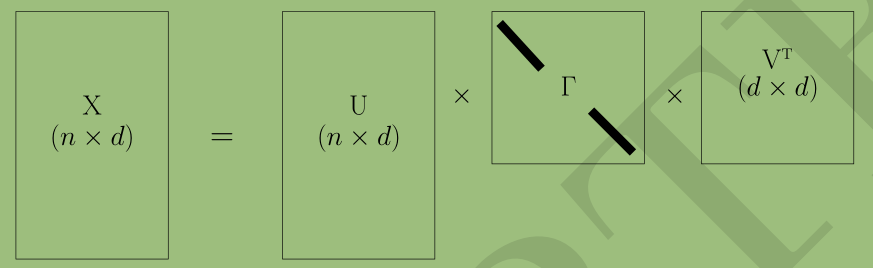
\(\mathtt{U}\)具有标准正交列(\(\mathtt{U^TU=E}\))
\(\mathtt{V}\)是一个正交矩阵(\(\mathtt{V^TV=E}\))
\(\Gamma\)是一个对角矩阵,其上的元素\(\gamma_i=\Gamma_{ii}\),\(\gamma_1\ge\gamma_2\ge....\ge\gamma_d\ge0\),\(\gamma_i\)称为\(\mathtt{X}\)的奇异值
\(\mathtt{U}\)包含的列称为\(\mathtt{X}\)的左奇异值向量,值\(\mathtt{V}\)包含的列称为\(\mathtt{X}\)的右奇异值向量
方阵将一个特征向量映射到它自身的一个倍数,更一般的非方阵将一个左(右)奇异向量映射到对应的右(右)的一个倍数。(左)奇异向量,由以下恒等式验证:
\(\mathtt{U^TX=\Gamma V^T},\mathtt{XV=U\Gamma}\)
算法
输入已经定心的数据\(\mathtt{X}\)
- 将\(\mathtt{X}\)进行奇异值分解计算出右奇异矩阵\(\mathtt{V}\)
- 取\(\mathtt{V}\)的前k列组成\(\mathtt{V_k}\)
- \(\mathtt{Z=XV_k}\),重构后的输入数据\(\mathtt{\hat{X}=XV_kV_k^T}\)