机器学习笔记（八）：PCA降维算法

1 - PCA概述

主成份分析，简称为PCA，是一种非监督学习算法，经常被用来进行

• 数据降维

• 有损数据压缩

• 特征抽取

• 数据可视化

2 - PCA原理详解

通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。

由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵，所以PCA算法有两种实现方法：

• 基于特征值分解协方差矩阵实现PCA算法
• 基于SVD分解协方差矩阵实现PCA算法。

2.1 - SVD具体介绍

2.2.1 - 特征值、特征向量、特征值分解

特征值分解和奇异值分解在机器学习中都是很常见的矩阵分解算法。两者有着很紧密的关系，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。

1）特征值、特征向量

如果一个向量v是矩阵A的特征向量，将一定可以表示成下面的形式：
$Av=\lambda v$
其中， $\lambda$是特征向量 $v$对应的特征值，一个矩阵的一组特征向量是一组正交向量

2）特征值与特征向量的几何意义

一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说下面的这个矩阵：
$M=\begin{bmatrix} 3 & 0\\ 0 & 1 \end{bmatrix}$
它其实对应的线性变换是如下形式：

因为这个矩阵M乘以一个向量（x,y）的结果是：
$\begin{bmatrix} 3 & 0\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} 3x\\ y \end{bmatrix}$
上面的矩阵是对称的，所以这个变换是一个对x、y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值大于1时是拉伸，当值小于1时是缩短），如图2所示。当矩阵不是对称的时候，假如说矩阵是下面的样子：
$\begin{bmatrix} 3 & 0\\ 0 & 1 \end{bmatrix}$
它所描述的变换是下面的样子：

这其实是在平面上对一个轴进行的拉伸变换，如图蓝色的箭头表示，蓝色的箭头是一个最主要的变换方向（变换的方向可能不止一个）。如果想要描述好一个变换，那我们就需要描述好这个变换的主要变换方向。

3）特征值分解

对于矩阵A，有一组特征向量v，将这组向量进行正交单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵A分解为如下式：
$A=Q\Sigma Q^{-1}$
其中，Q是矩阵A的特征向量组成的矩阵， $\Sigma$则是一个对角阵，对角线上的元素就是特征值。我们来分析一下特征值分解的式子，分解得到的 $\Sigma$矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变换方向（从主要的变化到次要的变化排列）

当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变换可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变化方向，我们通过特征值分解得到的钱N个特征向量，就对应了这个矩阵最重要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵变换，也就是之前说的：提取这个矩阵最重要的特征。

**总结：**特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多么重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多事情。不过，特征值分解也有很多局限，比如说变换的矩阵必须是方阵。

4）特征值分解的例子

这里我们用一个简单的方阵来说明特征值分解的步骤。我们的方阵A定义为：
$A=\begin{bmatrix} -1 & 1 & 0\\ -4 & 3 & 0\\ 1 & 0 & 2 \end{bmatrix}$
首先，由方阵A的特征方程，求出特征值
$|A-\lambda E|=\begin{bmatrix} -1-\lambda & 1 & 0\\ -4 & 3-\lambda 0 & 0\\ 1 & 0 & 2-\lambda \end{bmatrix}=（2-\lambda）\begin{bmatrix} -1-\lambda & 1 \\ -4 & 3-\lambda \end{bmatrix}=(2-\lambda)(\lambda-1)^2=0$

特征值为 $\lambda=2,1(重数是1)$。

然后，把每个特征值 $\lambda$代入线性方程组 $（A-\lambda E）x=0$,求出特征向量。

当 $\lambda=2$时，解线性方程组 $(A-2E)x=0$

$(A-2E)=\begin{bmatrix} -3 & 1 & 0\\ -4 & 1 & 0\\ 1 & 0 & 0 \end{bmatrix}\rightarrow \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix}$

解得 $x_1=0,x_2=0$,特征向量为： $p_1=\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}$

当 $\lambda=1$时，解线性方程组 $(A-2E)x=0$

$(A-E)=\begin{bmatrix} -2 & 1 & 0\\ -4 & 2 & 0\\ 1 & 0 & 1 \end{bmatrix}\rightarrow \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 2\\ 0 & 0 & 0 \end{bmatrix}$

解得 $x_1+x_3=0,x_2+2x_3=0$,特征向量为： $p_1=\begin{bmatrix} -1\\ -2\\ 1 \end{bmatrix}$

最后，方阵A的特征值分解为：
$A=Q\sum Q^{-1}=\begin{bmatrix} 0 & -1 & -1\\ 0 & -2 & -2\\ 1 & 1 & 1 \end{bmatrix}\begin{bmatrix} 2 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 0 & -1 & -1\\ 0 & -2 & -2\\ 1 & 1 & 1 \end{bmatrix}^{-1}$

2.2.2 SVD分解

1）特征值分解矩阵的缺点

我们前面讲了很多特征值、特征向量和特征值分解，而且基于我们以前学习的线性代数知识、利用特征值分解提取特征矩阵是一个容易理解并且便于实现的方法。但是为什么还存在奇异值分解呢？特征值分解最大的问题是只能针对方阵，即 $n*n$的矩阵，而在实际的应用中，我们分解的大部分都不是方阵。

举个例子：
关系型数据库中的某一张表的数据存储结构类似于一个二维矩阵，假设这个表有m行，有n个字段，那么这个表数据矩阵规模就是m*n。很明显，在绝大部分情况下，m和n是不相等的。如果这个时候要对这个矩阵进行特征提取，特征值分解的方法明显就不行了。此时，就可以用SVD对非方阵进行分解。

2） 奇异值分解

奇异值分解是一个能使用与任意矩阵的一种分解方式，对于任意矩阵A总是存在一个奇异值分解：
$A=U\Sigma V^T$

假设A是一个mn的矩阵，那么得到的U是一个mm的方阵，U里面的正交向量被称为左奇异向量。 $\Sigma$是一个mn的矩阵， $\Sigma$除了对角线其他元素都为0，对角线上的元素称为奇异值。 $V^T$是V的转置矩阵，是一个nn的矩阵，它里面的正交向量被称为右奇异值向量。而且一般来讲，我们会将 $\Sigma$上的值按从大到小的顺序排列。上面矩阵的维度变化可以参照下图所示。

**思考：**虽说上面奇异值分解等式成立，但是如何求得左奇异值向量、右奇异值向量和奇异值呢？
**答案：**由上面的奇异值分解等式，我们是不知道如何拆分矩阵A的。我们可以把奇异值和特征值联系起来。
首先，我们用矩阵A的转置乘以A，得到一个方阵，用这样的方阵进行特征分解，得到的特征值和特征向量满足下面的等式：
$(A^TA)v_i=\lambda_iv_i$
这里的 $v_i$就是我们要求的右奇异向量。
其次，我们将A和A的转置做矩阵的乘法，得到一个方阵，用这样的方阵进行特征分解，得到的特征和特征向量满足下面的等式：
$(AA^T)u_i=\lambda_iu_i$
这里的 $u_i$就是左奇异向量。
**思考：**上面我们说 $A^TA$的特征向量组成的矩阵是我们SVD中的V矩阵，而 $AA^T$的特征向量组成的就是我们SVD的U矩阵，这有什么根据么？我们来证明一下，以V举证的证明为例：
$A=U\Sigma V^T\Rightarrow A^T=V\Sigma^TU^T\Rightarrow A^TA=V\Sigma^TU^TU\Sigma V^T=V\Sigma^2V^T$

上式证明中使用了 $U^TU=I,\Sigma^T\Sigma=\Sigma^2$,可以看出， $A^TA$的特征向量组成的矩阵就是我们SVD中的V矩阵，而 $AA^T$的特征向量组成的就是我们SVD中的U矩阵。

补充定义：
$U\in M_n(R)满足U^TU=I，则U是实正交矩阵$
此外，我们还可以得到奇异值，奇异值求法有两种：

a)第一种：
$A=U\Sigma V^T\Rightarrow AV\Rightarrow U\Sigma V^TV\Rightarrow AV = U\Sigma\Rightarrow Av_i=\sigma u_i\Rightarrow \sigma_i=\frac{Av_i}{u_i}$

b)第二种

通过上面的证明，我们还可以看出，特征值举证等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：
$\sigma_i=\sqrt{\lambda_i}$
这里的 $\sigma_i$就是奇异值，奇异值 $\sigma_i$跟特征值类似，在矩阵 $\Sigma$中也是从大到小排列。

思考：
我们已经知道如何用奇异值分解任何矩阵了，那么问题又来了，一个mn的矩阵A，你把它分解成mm的矩阵U、mn的矩阵 $\Sigma$和nn的矩阵 $V^T$

这三个矩阵中任何一个的维度似乎一点也不比A的维度小，而且还要做两次矩阵的乘法，这不是把简单的事情变得更加复杂了吗？

答案：
在奇异值分解矩阵中 $\Sigma$里面的奇异值按从大到小的顺序排列，奇异值 $\sigma_i$从大到小的顺序减小的特别快。**在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上，也就是说，剩下的90%甚至99%的奇异值几乎没有什么作用。**因此，我们可以用前面r个打的奇异值来近似描述矩阵，于是奇异值分解公式可以写成如下：
$A_{m*n}\approx U_{m*n}\Sigma_{r*r}V_{r*n}^T$
其中r是一个远远小于m和n的数，右边的三个举证相乘的结果会将使一个接近A的矩阵。如果r越接近于n，则相乘的结果越接近于A。如果r的取值远远小于n，从计算机内存的角度来说，右边三个矩阵的存储内存要远远小于矩阵A的。所以在奇异值分解中r的取值很重要，就是在计算精度和事件空间之间做选择。

3）SVD计算举例

这里我们用一个简单的矩阵来说明奇异值分解的步骤。我们的矩阵A定义为：
$\begin{bmatrix} 0 & 1 \\ 1 & 1\\ 1 & 0 \end{bmatrix}$
首先，我们先求出 $A^TA$和 $AA^T$：

$A^TA=\begin{bmatrix} 0 & 1 &1\\ 1 & 1&0\\ \end{bmatrix}\begin{bmatrix} 0 & 1 \\ 1 & 1\\ 1 & 0 \end{bmatrix}=\begin{bmatrix} 2 & 1 \\ 1 & 2\\ \end{bmatrix}$

$AA^T=\begin{bmatrix} 0 & 1 \\ 1 & 1\\ 1 & 0 \end{bmatrix}\begin{bmatrix} 0 & 1 &1\\ 1 & 1&0\\ \end{bmatrix}=\begin{bmatrix} 1 & 1 &0\\ 1 & 2&1\\ 0 & 1& 1 \end{bmatrix}$
然后，求出 $A^TA$和 $AA^T$的特征值和特征向量：
$A^TA$的特征值和特征向量：
$\lambda_1=3; v_1=\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix};\lambda_2=1;v_2=\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}；$

$AA^T$的特征值和特征向量：
$\lambda_1=3;u_1=\begin{bmatrix} \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{bmatrix};\lambda_2=1;u_2=\begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{-1}{\sqrt{2}} \end{bmatrix};\lambda_3=0;u_3=\begin{bmatrix} \frac{1}{\sqrt{3}} \\ \frac{-1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{bmatrix};$
然后，我们直接使用 $\sigma_i=\sqrt{\lambda_i}$直接求出奇异值 $\sqrt{3}$和1。

最后，我们得到A的奇异值分解为：
$A=U\Sigma V^T=\begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & \frac{-1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}} & \frac{-1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix}\begin{bmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}$

2.2.3 SVD分解的应用

异值分解的应用有很多，比如：用SVD解PCA、潜在语言索引也依赖于SVD算法。可以说，SVD是矩阵分解、降维、压缩、特征学习的一个基础的工具，所以SVD在机器学习领域相当的重要。

1)降维:

通过奇异值分解的公式，我们可以很容易看出来，原来矩阵A的特征有n维。经过SVD分解后，可以用前r个非零奇异值对应的奇异向量表示矩阵A的主要特征，这样就把矩阵A进行了降维。

2)压缩:

通过奇异值分解的公式，我们可以看出来，矩阵A经过SVD分解后，要表示原来的大矩阵A，我们只需要存储U、Σ、V三个较小的矩阵即可。而这三个较小规模的矩阵占用内存上也是远远小于原有矩阵A的，这样SVD分解就起到了压缩的作用。

2.2 - 协方差和散度矩阵

样本均值：

$\bar x = \frac{1}{n}\sum_{i=1}^Nx_i$

样本方差：
$S^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar x)^2$

样本X和样本Y的协方差

$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)$

由上面的公式，我们可以得到以下结论：

（1）方差的计算公式是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征；方差是协方差的特殊情况。

（2）方差和协方差的除数是n-1，这是为了得到方差和协方差的无偏估计。

协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上式协方差矩阵（对称方阵）。例如，对于3维数据（x,y,z），计算它的协方差就是：
$Cov(X,Y,Z)=\begin{bmatrix} Cov(x,x) & Cov(x,y) &Cov(x,z) \\ Cov(y,x) & Cov(y,y) & Cov(y,x)\\ Cov(z,x) & Cov(z,x) & Cov(z,z) \end{bmatrix}$

散度矩阵定义为：
$S=\sum_{k=1}^n(x_k-m)(x_k-m)^T$

$m=\frac{1}{n}\sum_{k=1}^nx_k$

对于数据X的散度矩阵为： $XX^T$

其实协方差矩阵和三都矩阵关系密切，散度矩阵就是协方差矩阵乘以（总数据量-1）。因此它们的特征值和特征向量是一样的。这里值得注意的是，散度矩阵是SVD奇异值分解的一步，因此PCA和SVD是由很大联系的。

3 - PCA算法两种实现方法

3.1 - 基于特征值分解协方差矩阵实现PCA算法

输入数据集：
$X=\{x_1,x_2,x_3,\dots,x_n\}$

需要降到K维

1）去平均值（即去中心化），即每一位特征减去各自的平均值

2）计算协方差矩阵 $\frac{1}{n}XX^T$

注：这里除或不除n或n-1，其实对求出的特征向量没有影响。

3）用特征值分解方法求协方差矩阵

$\frac{1}{n}XX^T$的特征值与特征向量。

4）对特征值从大到小排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5）将数据转换到k个特征向量构建的新空间中，即Y=PX。

例子

$X=\begin{bmatrix} -1 & -1 & 0 &2 & 0\\ -2 & 0 & 0 &1 & 1 \end{bmatrix}$

以X为例，我们用PCA方法将这两行数据降到一行。

1）因为X矩阵的每行已经是零均值，所以不需要去平均值。

2）求协方差矩阵：

$C=\frac{1}{5}\begin{bmatrix} -1 & -1 & 0 &2 & 0\\ -2 & 0 & 0 &1 & 1 \end{bmatrix}\begin{bmatrix} -1 & -2\\ -1 & 0\\ 0 & 0\\ 2 & 1\\ 0&1 \end{bmatrix}=\begin{bmatrix} \frac{6}{5} & \frac{4}{5}\\ \frac{4}{5}&\frac{6}{5} \end{bmatrix}$

3）求协方差矩阵的特征值与特征向量。

求解后的特征值为：
$\lambda_1=2,\lambda_2=\frac{2}{5}$

对应的特征向量为：

$c_1=\begin{bmatrix} 1\\ 1 \end{bmatrix},c_2=\begin{bmatrix} -1\\ 1 \end{bmatrix}$

其中对应的特征向量分别是一个通解 $c_1$和 $c_2$可以取任意实数。那么标准化后的特征向量为：
$\begin{bmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{bmatrix},\begin{bmatrix} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{bmatrix}$

4）求得矩阵P为：
$P=\begin{bmatrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{bmatrix}$

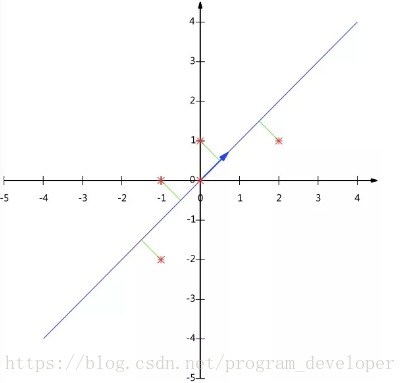
5)最后我们用P的第一行乘以数据矩阵X，就得到了降维后的表示：
$Y=\begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}\begin{bmatrix} -1 & -1 & 0 &2 & 0\\ -2 & 0 & 0 &1 & 1 \end{bmatrix}=\begin{bmatrix} -\frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}}&0&\frac{3}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{bmatrix}$

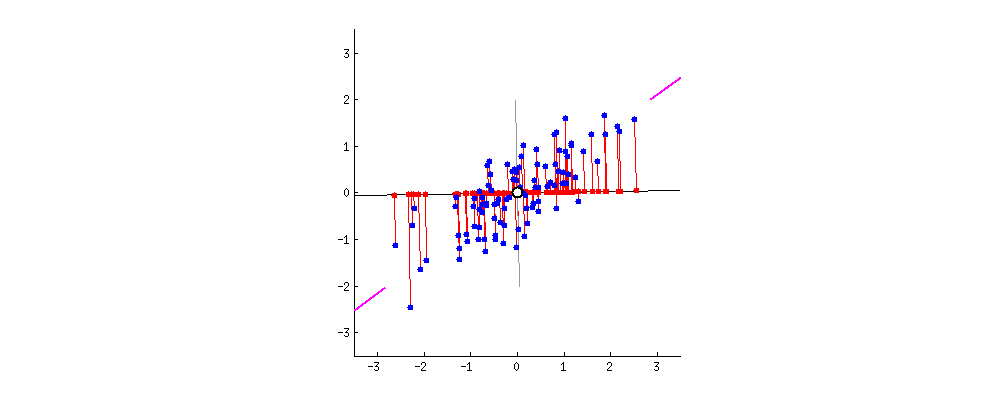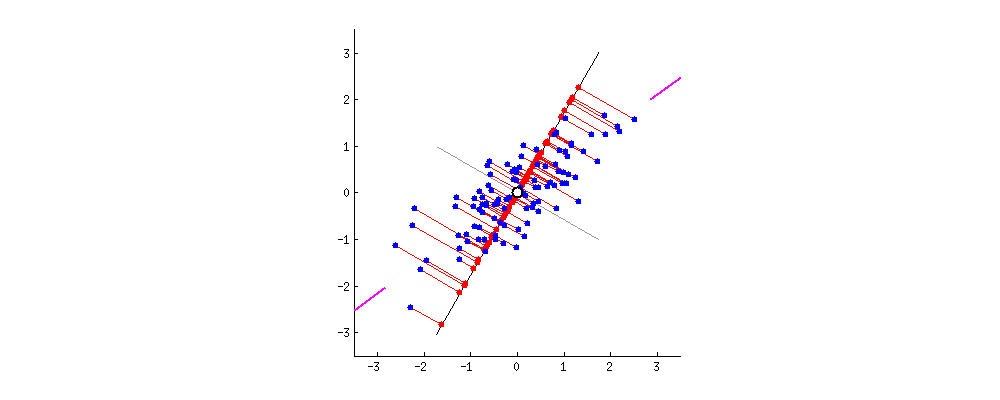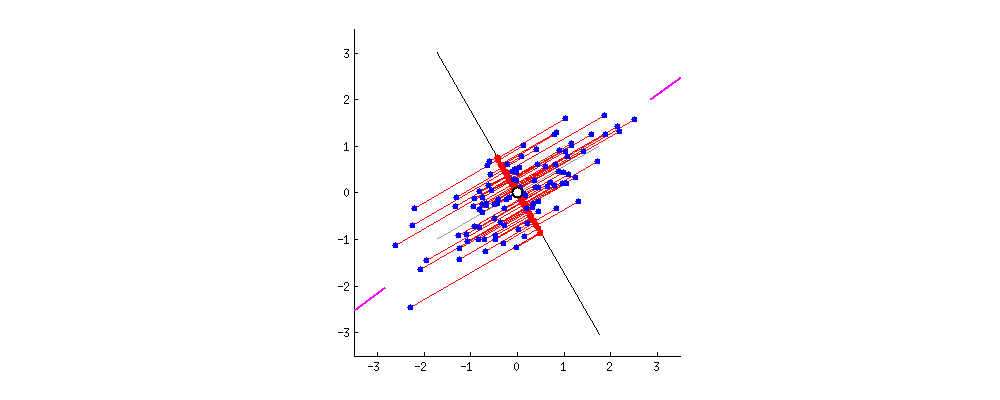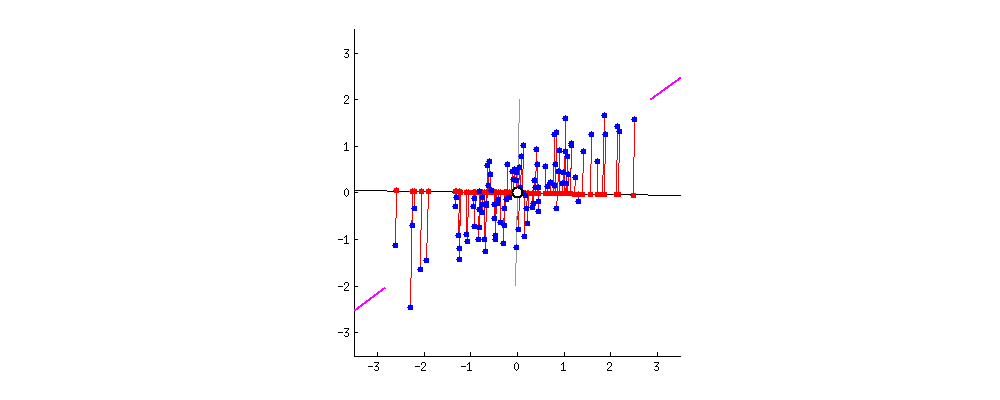
效果如下图所示

注意：
如果我们通过特征值分解协方差矩阵，那么我们只能得到一个方向的PCA降维。这个方向就是对数据矩阵X从行（或列）方向上压缩降维。

3.2 基于SVD分解协方差矩阵实现PCA算法

输入数据集：
$X=\{x_1,x_2,x_3,\dots,x_n\}$

需要降到K维

1）去平均值（即去中心化），即每一位特征减去各自的平均值

2）计算协方差矩阵 $\frac{1}{n}XX^T$

注：这里除或不除n或n-1，其实对求出的特征向量没有影响。

3）用SVD计算协方差矩阵

$\frac{1}{n}XX^T$的特征值与特征向量。

4）对特征值从大到小排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5）将数据转换到k个特征向量构建的新空间中，即Y=PX。

在PCA降维中，我们需要找到样本协方差矩阵 $XX^T$的最大K个特征向量，然后用这个最大的K个特征向量组成的矩阵来做低维投影降维。

当样本数多、样本特征数也多的时候，这个计算还是很大的。

当我们用SVD分解协方差矩阵的时候SVD有两个好处：

• 1.有一些SVD的实现算法可以先不求出协方差矩阵 $XX^T$也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解而是通过SVD来完成，这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征值分解。

• 2.注意到PCA仅仅使用了我们SVD的左奇异矩阵，没有使用到右奇异值矩阵，那么右奇异值矩阵有什么用呢？假设我们的样本是 $m*n$的矩阵X，如果我们通过SVD找到了矩阵 $X^TX$最大的k个特征向量组成的 $k*n$的矩阵 $V^T$,则我们可以做如下处理： $X^{'}_{m*k}=X_{m*n}V_{n*k}^T$，可以得到一个 $m*k$的矩阵 $X^{'}$,这个矩阵和我们原来 $m*n$的矩阵X相比，列数从n减到了K,可见对列数进行了亚索，也就是说，左奇异矩阵可以用于对行数的压缩；右奇异矩阵可以用于对列（即特征维度）的压缩。这就是我们用SVD分解协方差矩阵实现PCA可以得到两个方向的PCA降维（即行和列两个方向）。

4 - Python实现PCA算法

##Python实现PCA
import numpy as np
import matplotlib.pyplot as plt
def pca(X,k):#k is the components you want
  #mean of each feature
  n_samples, n_features = X.shape
  mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
  #normalization
  norm_X=X-mean
  #scatter matrix
  scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
  #Calculate the eigenvectors and eigenvalues
  eig_val, eig_vec = np.linalg.eig(scatter_matrix)
  eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
  # sort eig_vec based on eig_val from highest to lowest
  eig_pairs.sort(reverse=True)
  # select the top k eig_vec
  feature=np.array([ele[1] for ele in eig_pairs[:k]])
  #get new data
  data=np.dot(norm_X,np.transpose(feature))
  return data

X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
X_pca=pca(X,1)
X_pca

array([[-0.50917706],
[-2.40151069],
[-3.7751606 ],
[ 1.20075534],
[ 2.05572155],
[ 3.42937146]])