4.1 多维特征
上一章节学习了单变量/特征的回归模型,现在对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为
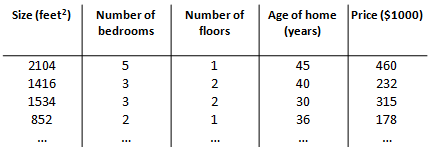
增添更多特征后,我们引入一系列新的注释:
n 代表特征的数量
代表第
个训练实例,是特征矩阵中的第
行,是一个向量(vector)。
比如:
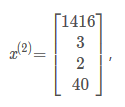
代表特征矩阵中第
行的第
个特征,也就是第
个训练实例的第
个特征。
支持多变量的假设 表示为:
公式中有n+1个参数和n个变量。为简便起见,引入变量,公式变为
此时模型中的参数是一个n+1维的向量,任何一个训练实例也都是n+1维的向量,特征矩阵X的维度是 m∗(n+1)。 因此公式可以简化为:,其中上标T代表矩阵转置。
4.2 多变量梯度下降
下面介绍使用梯度下降算法,解决多特征的线性回归问题。
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
cost function:
其中:
而梯度下降法:
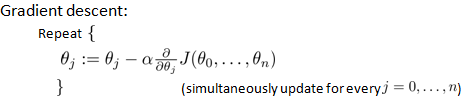
下面就是多变量的梯度下降法的计算过程(观察可以发现,与单变量的梯度下降法是很相似的):

4.3 特征下降算法之特征缩放(feature scaling)法
在解决多维特征问题时,如果我们能够确保特征的取值在一个相似的范围中,那么梯度下降算法就能够更快的收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
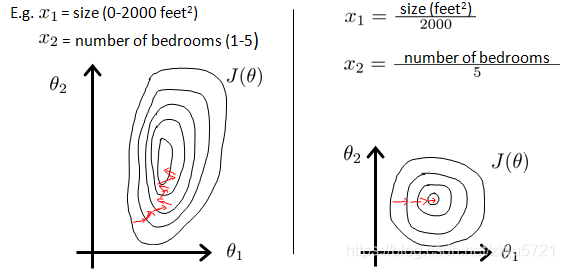
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。
一般来说,数值在-3到3之间,或是-1/3到1/3之间,都是可以接受的。
特征缩放时,除了除以范围的最大值时,通常还可以采用一种叫均值归一化的方法:
给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1。转化函数为,其中
是平均值,
是标准差(实际使用时,其实可以直接用最大值减去最小值就可以,---即范围)。
4.4 特征下降算法之学习速率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
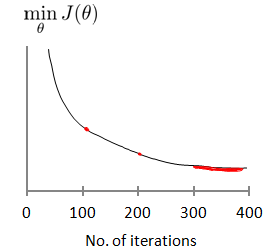
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如0.001)进行比较,但通常看上面这样的图表更好。
梯度下降算法的每次迭代受到学习率的影响,如果学习率a过小,则达到收敛所需的迭代次数会非常高;如果学习率a过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率:α=0.01,0.03,0.1,0.3,1,3,10
4.5 特征和多项式回归
如房价预测问题,,
,
,
,则
,
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型或者三次方模型,如图:
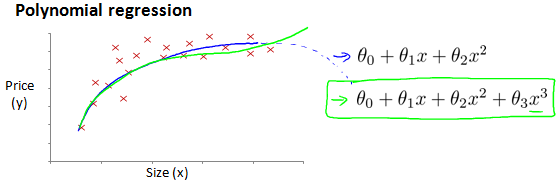
通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外,我们可以令,
,从而将模型转化为线性回归模型
根据函数图形特性,我们还可以使:
或者:
如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
4.6 正规方程
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案。如:
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的: 。
假设我们的训练集特征矩阵为 X(包含了 x0=1)并且我们的训练集结果为向量 y,则利用正规方程解出向量
以下表示数据为例:
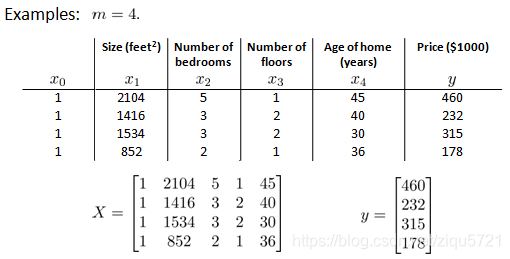
运用正规方程方法求解参数:
推导过程如下:
,其中,
将向量表达形式转为矩阵表达形式,则有,其中X为m行n列的矩阵(m为样本个数,n为特征个数),θ为n行1列的矩阵,y为m行1列的矩阵,对J(θ)进行如下变换
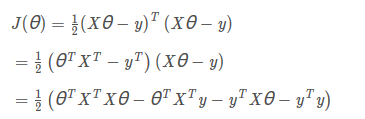
接下来对J(θ)求偏导,需要用到以下几个矩阵的求导法则:

梯度下降法和正规方程组法的比较:

总结一下,矩阵相乘的时间复杂度为 ,只要特征变量的数目并不大,标准方程是一个很好的计算参数θ的替代方法。根据吴恩达老师的经验,特征变量数量小于一万,通常使用标准方程法,超过一万时可以考虑使用梯度下降法。
参考资料: