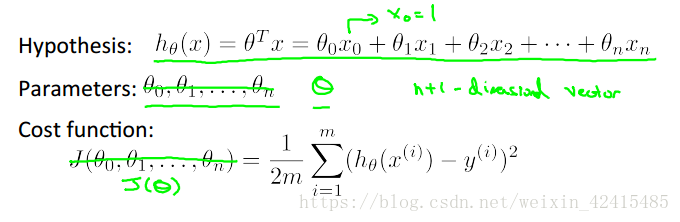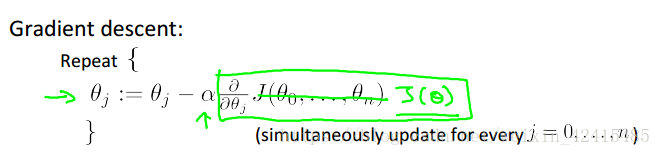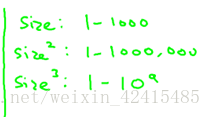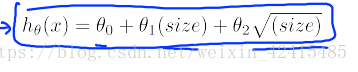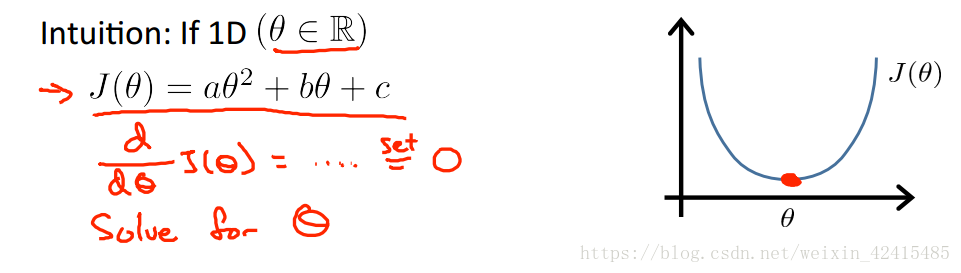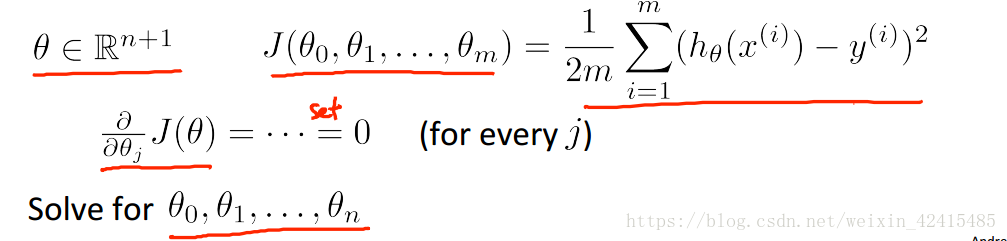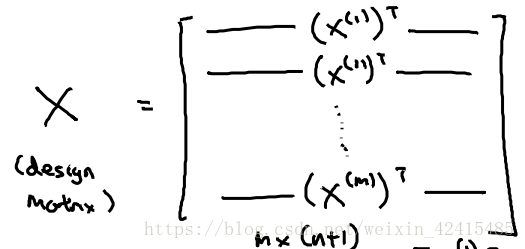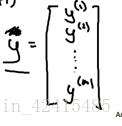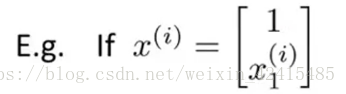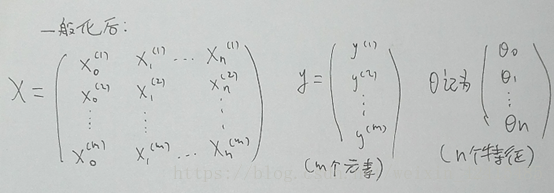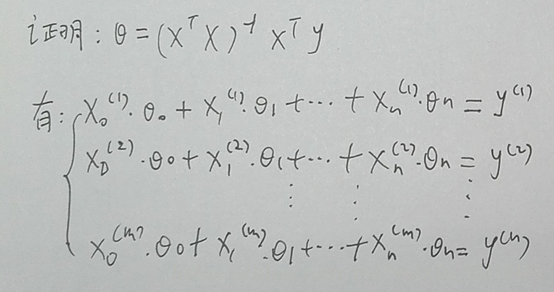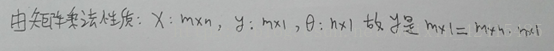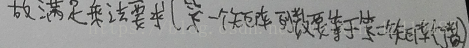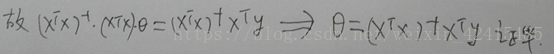吴恩达机器学习学习笔记第五章：多变量线性回归

1.Multiple features多特征

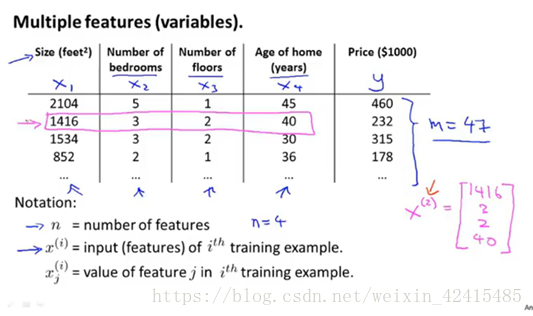
现在我们有多个特征了，比如还是预测房子价格X不仅仅是面积大小还有卧室数量，楼层数量以及房子的年龄

 

 

表达形式的记法：

n=4即有4个特征（总面积 卧室数量 楼层数 房子年龄）

m=47即有47个样本（47个房子）

x^(i)表示第i（i不是次方而是对应训练集的索引）条样本对的特征 如x^(2)就是粉色的 这样表示他就是一个四维向量

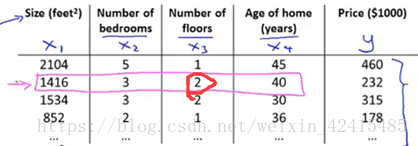
x^(i)j表示：如i=2 j=3就是红圈

这里的记号最好能很快反应过来 不然编程的时候会比较费时                                      

再来看看线性回归的假设函数

Eg是对这个图Andrew老师把θ举了个特值的例子：

（Eg是把参数θ取特值的例子）

（一个房子的基本价格是8千，每平方米0.1（百美元），……,-2x4即随年度使用价钱贬值）

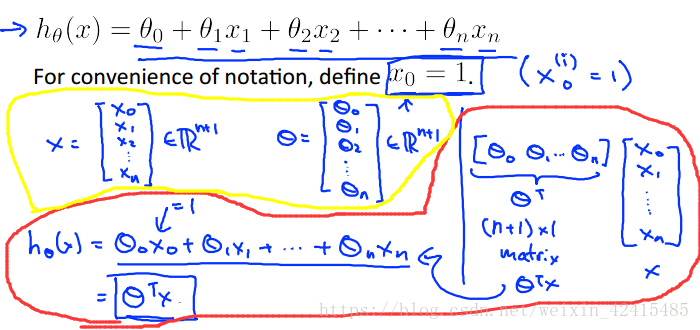
当然特征个数为n时就如下了：                  

我们和单变量的做法一样令他θ0的系数x^(i)0全部=1

所以现在X和θ都是一个n+1维向量 （黄圈）

那么假设函数就可以写成内积了（红圈）

 

 

2.多元梯度下降法：

  假设函数、参数、代价函数书写如下：

然后执行梯度下降

左边是之前学的单变量 右边是多变量其实本质是一样的

因为我仍然是线性回归我没有什么二次项系数这种奇奇怪怪的东西，都是一次的所以θ1~θn求导结果的构造上都是一样的

 

3.多元梯度下降法的特征缩放：

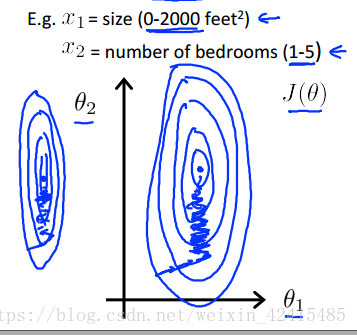
如果你不同特征之间的取值范围差距很大 如面积是0~2000 而寝室数量是1~5

我们画出来代价函数的等值线就会变成这种又长又扁的椭圆 这会极大的降低我们做梯度下降的速度 并且可能会导致来回波动的情况

 

针对这种情况我们就要做特征缩放：

 

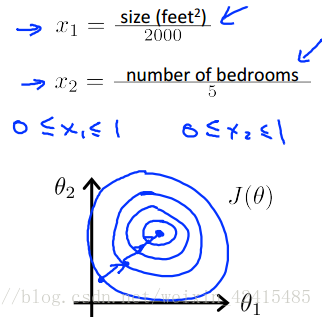
方法一是用特征值除以范围的最大值

这样做以后等值线就没有那么偏移了 看起来更圆了

 

特征范围的设置没有具体的要求，但是像-100~100、-0.0001~0.0001这种显然就没有-3~3、-2~0.5这种好 

 

方法二叫：均值归一化（Mean normalization）

用X减去均值（μ）除以极差（max-min）

 

方法三：X减去均值除以标准差(就像标准正态分布一样) （正态分布忘了的可以去找概率论、统计学的书看看）

 

4.多元梯度下降法的学习率：

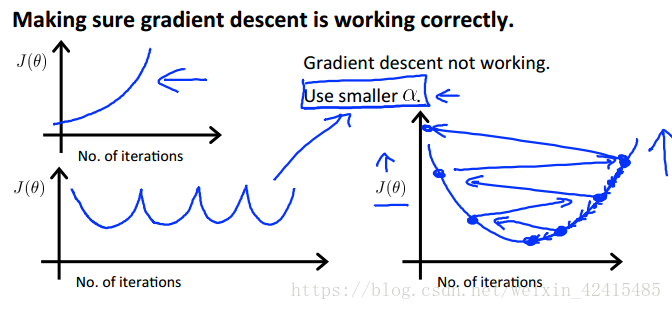
如果学习率过大，J(θ)可能越来越大甚至不收敛，如果过小，J(θ)的迭代速率会很慢。

这些都是学习率过大的情况（图像的X轴是迭代次数 Y轴是J(θ)的值）

一般认定如果J(θ)迭代中下降到小于某一个值，例如10的负3次方，我们就说他收敛，不需要再进行继续迭代了，但是这个下界不是那么好选

如果我们的梯度下降没有正常工作 那么检查学习率 并合理的修正学习率（用尝试法：若小了就……0.001→0.01→0.1…… 若发现0.01小了 而0.1大了 就试试0.03……）

 

 

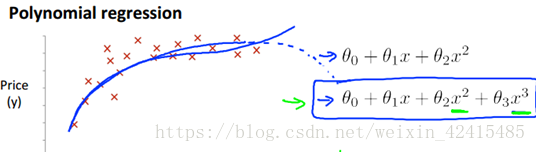
5.特征和多项式回归

除了1阶的这种线性回归我们还可以弄出2次方、3次方这样的多项式回归

比如有宽度又有长度这两个 那我们想把长度乘宽度=面积作为特征去拟合我们的数据

对多项式回归 归一化就非常重要了

6.正规方程

它是一种区别于迭代法用来求θ的直接解法，可以说只需要一步就能求出θ的最优值

对于这种θ是常数的例子直接求导令导数为0就能得到最优解

而下面的θ是n+1维向量，J（θ）是这个向量的函数

如果我对所有θj一个一个的做偏微分那就太蠢了

 

在样本中加一列θ0=1 并写出所有特征向量Xi对应的矩阵 再把y写出向量

X是一个m*(n+1)维矩阵 X也称为设计矩阵（design matrix） 即把每一个训练样本

进行转置后放到每一行

 

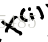
 y是一个m维向量 (m是训练样本数量 n是特征变量个数)

设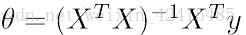 就能得到使得代价函数最小化的θ

 

举个具体的例子：

我的 除了 外只有一个特征变量，

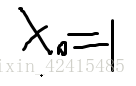
这样的 就写出了这样的设计矩阵：

 

上面比较混乱。我们用笔再写写书写表示方法

以及θ=XXXX那个公式在线性代数的证明（书写较差尽情原谅）

 

梯度下降法与正规方程法的优缺点对比：

梯度下降法的缺点：

(1)需要选择学习率a 也就意味着你需要运行多次去找哪个学习率是使运行效果最好的

(2)需要很多次迭代(运算速度就慢了)

梯度下降法的优点：

(1)不管特征数量是几千量级还是几百万量级，梯度下降法都能很好的工作

(2)除了线性回归(Linear Regreesion)外，其他复杂的算法

 

 

正规方程法的优点：

(1)不需要自己找学习率a

(2)不需要迭代

(3)由于不需要找a不需要迭代所以就不需要画J（θ） 的曲线去检查收敛性了

(4)不需要进行特征缩放(我的特征变量x1是0~1 ，x2是-10000~10000这种都无所谓)

 

正规方程法的缺点：

(1)正规方程法一般用在线性回归上，不适用或者不能用在后续课程中讲到的更复杂算法

(2)当特征变量太多时会导致运算速度很慢：

正规方程法的计算成本的时间复杂度是O（n^3）

因为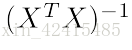 是一个n*n的矩阵（假设有n个特征变量）而计算一个逆矩阵的复杂度是以矩阵维度的3次方增长的，就算一个很好的计算方法也是只能做到接近n的3次方。这意味着当特征很多的时候 所需要耗费的时间代价就很大了 一般来说n不大于10000计算机都可以胜任正规方程法 但是再往上走就会考虑梯度下降法了

 

7.正规方程在矩阵不可逆时的解决方法：

首先第一个出现不可逆的原因一般是X里至少存在一组线性相关的特征变量比如X1是平方米X2是英尺 1平米=3.28英尺

第二个原因是你有很多特征具体的说就算m小于或等于n时，譬如说m=10 n=100 θ就算一个101维的向量 你要从10个训练样本中找到101个参数值，一般来说很难成功

 

当出现这种m小于n的情况我们考虑能否删除一些特征或者使用一种叫正则化（后面章节会讲）的方法  

在数值计算这门课中

Python中有numpy.linalg的线性代数库直接计算这种”伪逆”即：即使矩阵不可逆也能计算出他的逆:

inv(A)     计算方阵A的逆

pinv(A)    计算矩阵A的Moore-Penrose伪逆