四、多变量线性回归
4.1 多维特征与多变量梯度下降
4.2 梯度下降法实践1-特征缩放(Feature Scaling)
保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。
我觉得其实就是正则化，将数据控制在 [-1，1] 之间，这样数据的差距就相对减小很多
当然这种方式是在不同的特征值的范围差距十分大的时候使用才有明显作用
eg: size = (0, 2000) ==> size = (size - 1000) / 2000 ==> size = (-1, 1)
x = (x - 均值) / 标准差
# 特征缩放
def normalize_feature(df):
"""Applies function along input axis(default 0) of DataFrame."""
return df.apply(lambda column: (column - column.mean()) / column.std())
4.3 梯度下降法实践2-学习率
如何选择学习率
看梯度下降的曲线图
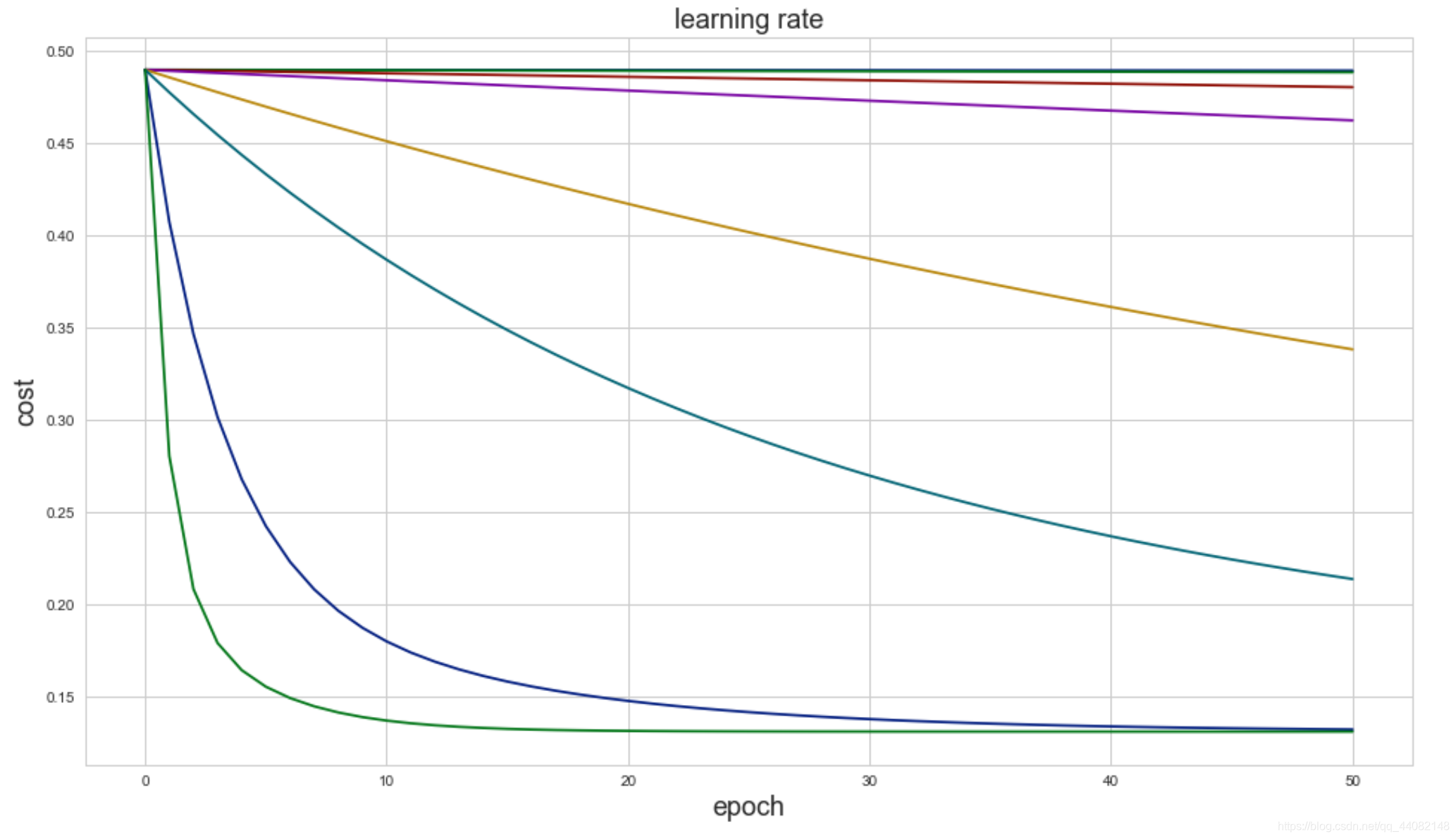这张图中显然绿色线代表的学习率更好
4.4 特征和多项式回归
其实就是可以通过将参数另外进行整理替换最后得到不同的回归方程的过程
如房价预测问题，可以将房子的长，宽两个参数整合成面积以方便拟合计算
h θ ( x ) = θ 0 + θ 1 × f r o n t a g e + θ 2 × d e p t h h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}\times{frontage}+{\theta_{2}}\times{depth} hθ(x)=θ0+θ1×frontage+θ2×depth
x 1 = f r o n t a g e {x_{1}}=frontage x1=frontage（临街宽度）， x 2 = d e p t h {x_{2}}=depth x2=depth（纵向深度）， x = f r o n t a g e ∗ d e p t h = a r e a x=frontage*depth=area x=frontage∗depth=area（面积），则： h θ ( x ) = θ 0 + θ 1 x {h_{\theta}}\left( x \right)={\theta_{0}}+{\theta_{1}}x hθ(x)=θ0+θ1x。
4.5 正规方程(Normal equation)
θ j : = θ j − α [ 1 m ∑ i = 1 m h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_{j}}:={\theta_{j}}-\alpha[\frac{1}{m}\sum\limits_{i = 1}^{m}h_\theta(x^{(i)}) - y^{(i)})x^{(i)}_j+\frac{\lambda}{m}\theta_j] θj:=θj−α[m1i=1∑mhθ(x(i))−y(i))xj(i)+mλθj]
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率α | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量n大时也能较好适用 | 需要计算 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为 O ( n 3 ) O(n^3) O(n3)，通常来说当n小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型，不适合逻辑回归模型等其他模型 |