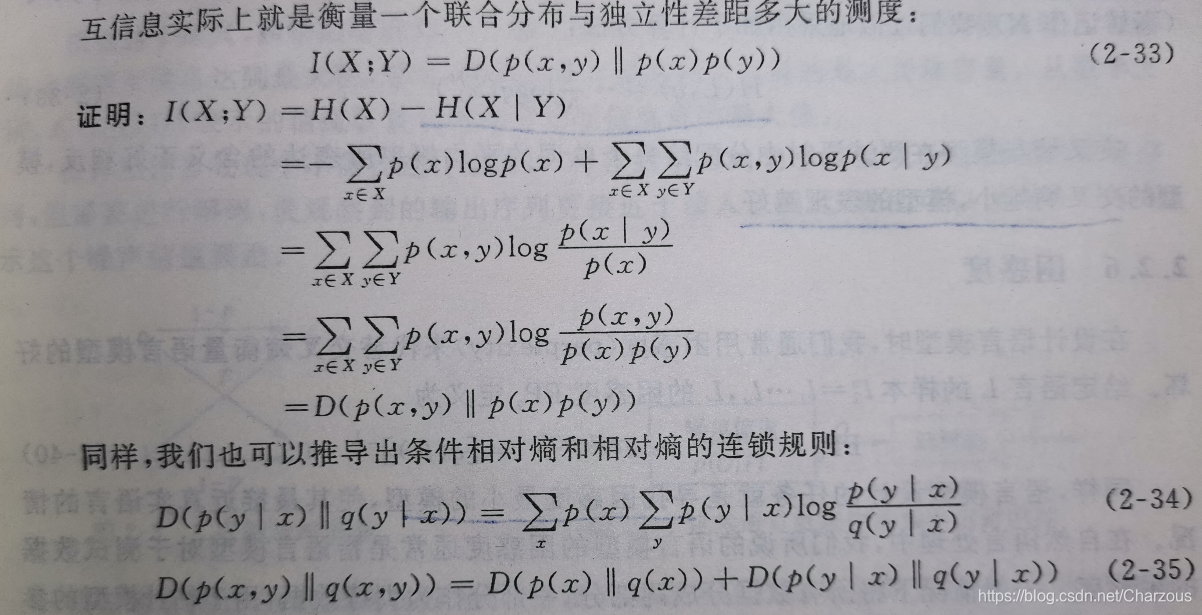熵、联和熵与条件熵、交叉熵与相对熵是什么呢？来这里有详细解读！

熵是一个很常见的名词，在物理上有重要的评估意义，自然语言处理的预备知识中，熵作为信息论的基本和重点知识，在这里我来记录一下学习的总结，并以此与大家分享。

1、熵

熵也被称为自信息，描述一个随机变量的不确定性的数量。熵越大，表明不确定性越大，所包含的信息量也越大，就说明很难去预测事件行为或者正确估值。
熵的公式定义：
X为一个离散型随机变量，其概率分布是p(x)=P(X=x),x $\in$ R,R为x取值空间，则X的熵 H(x) = — $\displaystyle\sum_{x \in R} p(x)log_2p(x)$ 公式(1)，单位是比特（bit）。
举例：

假设a,b,c,d,e,f 6个字符在一条语句中随机出现，每个字符出现的概率分别为： $\frac{1}{8}、\frac{1}{4}、\frac{1}{8}、\frac{1}{4}、\frac{1}{8}和\frac{1}{8}$。那么，每个字符的熵为多少？

H( p ) = — $\displaystyle\sum_{x \in \{a,b,c,d,e,f\}} p(x)log_2p(x)$ = -[ $4\times\frac{1}{8}log_2\frac{1}{8}+2\times\frac{1}{4}log_2\frac{1}{4}$] = 2.5(bit)
这里计算将相同概率的字符合并计算，结果表明什么呢？
结果说明传输一个字符平均只需要2.5个比特：

字符	a	b	c	d	e	f
编码	100	00	101	01	110	111

2、联和熵与条件熵

联和熵描述一对随机变量平均所需要的信息量。
公式定义：
随机变量X，Y~p(x,y)，X，Y的联和熵 $H(X,Y) = —\displaystyle\sum_{x\in X} \displaystyle\sum_{y\in Y} p(x)logp(x,y)$ 公式(2)

与之联系密切的条件熵指的是：给定X的情况下，Y的条件熵为：
$H(Y|X) = \displaystyle\sum_{x\in X} p(x)H(Y|X=x)=\displaystyle\sum_{x\in X} p(x) [-\displaystyle\sum_{y\in Y} p(y|x)logp(y|x)]=—\displaystyle\sum_{x\in X} \displaystyle\sum_{y\in Y} p(x,y)logp(y|x)$ 公式(3)
将以上公式（1）化简可以得到 $H(X,Y) =H(X) +H(Y|X)$ 公式(4)，被称为熵的连锁规则。
推广到一般情况，有 $H(X_1,X_2,···,X_n) =H(X_1) +H(X_2|X_1)+H(X_3|X_1,X_2)+···+H(X_n|X_1,···,X_{n-1})$

3、互信息

熵的连锁规则 $H(X,Y) =H(X) +H(Y|X)=H(Y) +H(X|Y)$,所以 $H(X) - H(X|Y)=H(Y)-H(Y|X)$，这个差就成为互信息，记作 $I(X;Y)$ 。

$在图中I(X;Y)反映的是已知Y的值后X的不确定性的减少量。$简而言之，Y的值透露了多少关于X的信息量。
因为H(X|X)=0，所以H(X)=H(X)-H(X|X)=I(X;X)，这公式推导说明了熵也成为自信息的概念，也说明两个完全相互依赖的变量之间的互信息并不是一个常量，而是取决定于它们的熵。
实际应用： 互信息描述了两个随机变量之间的统计相关性，平均互信息是非负的，在NLP中用来判断两个对象之间的关系，比如：根据主题类别和词汇之间的互信息进行特征提取。另外在词汇聚类、汉语自动分词、词义消岐、文本分类等问题有着重要用途。

4、交叉熵与相对熵

相对熵简称KL差异或KL距离，衡量相同时间空间里两个概率分布相对差异的测度。两个概率分布p(x)和q(x)的相对熵定义为 $D(p||q) = \displaystyle\sum_{x \in X} p(x)log_2\frac{p(x)}{q(x)}$
另外， $0log(0/q)=0,plog(p/0)=\infty$.期望值为 $D(p||q)=E_p(log\frac{p(x)}{q(x)})$

根据公式可知，当两个随机分布完全相同时，即p=q,其相对熵为0。当两个随机分布差别增加，相对熵的期望值也增大。
相对熵与互信息的联系如下证明：

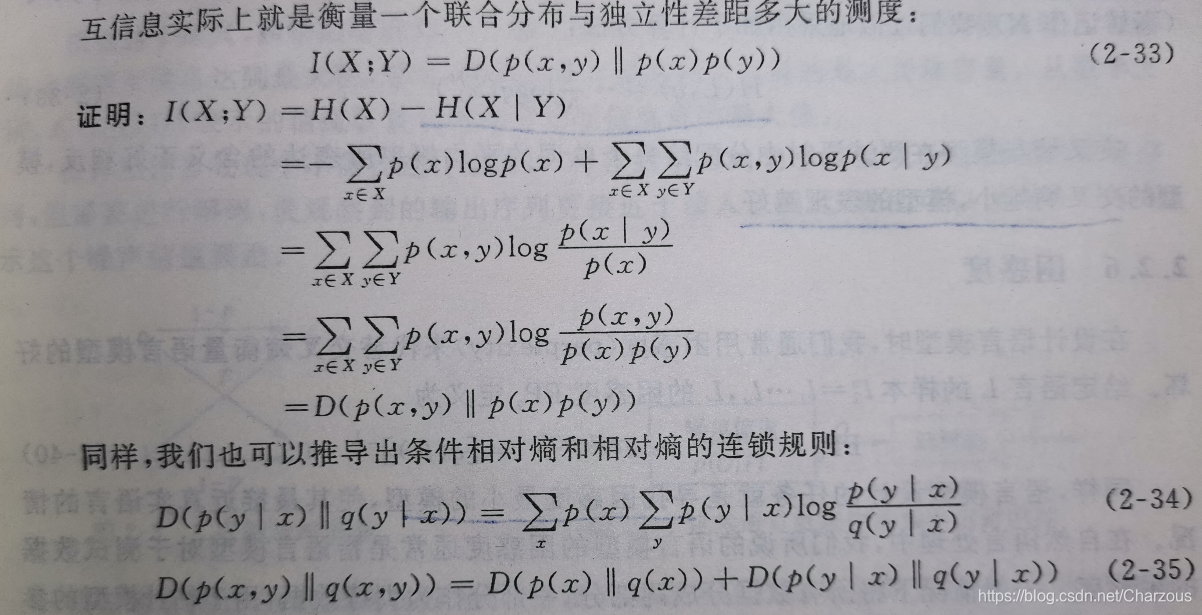
交叉熵就是机器学习中经常提到的一种熵的计算。它到底是什么呢？

交叉熵是衡量估计模型与真实概率分布之间之间差异情况。
如果一个随机变量X~ $p(x),q(x)$为用于近似 $p(x)$的概率分布，则实际p与模型q之间的交叉熵定义为：
$H(X,q)=H(X)+D(p||q)=-\displaystyle\sum_xp(x)logq(x)=E_p(log\frac{1}{q(x)})$

这里我们定义语言 $L=(X)$~ $p(x)$与其模型q的交叉熵为：

$H(L,q)=-\lim_{n \to \infty}\frac{1}{n}\displaystyle\sum_{x_1^n}p(x_1^n)logq(x_1^n)$
在理想的状态下，可以将L与q模型的交叉熵简化为：
$H(L,q)=-\lim_{n \to \infty}\frac{1}{n}logq(x_1^n)$

在设计模型q时候，目的是使交叉熵最小，这样模型的表现更好，从而使模型更接近最真实的概率分布 $p(x)$,一般的，当样本足够大时候，上面计算近似为： $H(L,q)=-\frac{1}{N}logq(x_1^N)$

5、困惑度

在设计语言模型，通常用困惑度（ $perplexity$）来代替交叉熵衡量语言模型的好坏。

假设语言L样本 $l_1^n=l_1\dots l_n,则L$的困惑度 $PP_q=2^{-\frac{1}{n}logq(l_1^n)}=[q(l_1^n)]^{-\frac{1}{n}}$

所以，寻找困惑度最小的模型成为模型设计的任务，通常指的是模型对于测试数据的困惑度。

6、总结

在信息论的熵部分，我们学到了什么呢？开始说到，这是NLP基础，也是入门机器学习的重要理论部分。

1. 熵（自信息）：描述一个随机变量的不确定性的数量。熵越大，表明不确定性越大，所包含的信息量也越大，就说明很难去预测事件行为或者正确估值。
2. 联和熵：描述一对随机变量平均所需要的信息量。
3. 条件熵：给定X的情况下，通过联和熵计算Y的条件熵，类似于条件概率思想。由此引出互信息概念。
4. 相对熵：简称KL差异或KL距离，衡量相同时间空间里两个概率分布相对差异的测度，与互信息密切相关。
5. 交叉熵：衡量估计模型与真实概率分布之间之间差异情况。

学习之后的一些记录，发现这部分知识在其他方面经常提及到，却不知其原理知识，因此做了一个简单的总结备忘，与尔共享！

我的博客园：熵、联和熵与条件熵、交叉熵与相对熵是什么呢？详细解读这里有！
我的CSDN博客：熵、联和熵与条件熵、交叉熵与相对熵是什么呢？来这里有详细解读！