离散数学——第三章 关系

第三章 关系

3.1.1.本章概述

关系的定义、关系的五大性质、关系的组成和复合、关系的矩阵表示、关系图表示；
三种闭包；
等价关系、等价类、划分
偏序、字典序、哈斯图、偏序集中的特殊元素

3.2.关系

3.2.1关系的概念

• 定义：
  集合A到B的二元关系R为 $A\times B$的子集，用于刻画A中的元素和B中的元素的对应关系。
  关系实质上是序偶 (x,y)的集合，其中序偶的第一个元素来自集合A,第二个元素来自集合B。

• 关系与集合、函数的联系
  关系本质是集合，是序偶的集合。
  函数是特殊的关系，或者说关系使我们所熟悉的函数的拓展。因为函数要求**定义域(domain)**里面的每一个元素都有与之对应的元素，但关系不要求。

• 一个有限集合上的二元关系的个数
  $A\times A$有 ${\vert A \vert}^2$个元素，也就说有 ${\vert A \vert}^2$个序偶， $A\times A$这个笛卡尔积的幂集里面的元素都是一种关系，所以 $A$上共有 $2^{{\vert A \vert}^2}$个关系。

3.3.2.关系的性质

• 自反性(reflexive)
  定义：
  设 $R$ 为定义在集合 $X$ 上的二元关系，如果对于每个 $x\in X$ ，有 $xRx$ ，则称二元关系 $R$ 是自反的。
  $\forall x[x\in A \rightarrow (x,x)\in R]$
• 反自反性(irreflexive)
  定义:
  设 $R$ 为定义在集合 $X$ 上的二元关系，如果对于每个 $x\in X$ ，都有 $\langle x,x \rangle \notin R$ ，则 $R$ 称作反自反的。
  $\forall x[x\in A \rightarrow (x,x)\notin B]$

显然，由定义可知，一个不是自反的关系，不一定就是反自反的。

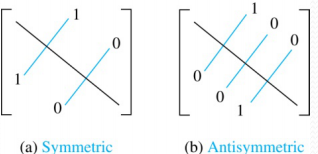
• 对称性(symmetric)
  定义：
  设 $R$ 为定义在集合 $X$ 上的二元关系，如果对于每个 $x,y\in X$ ，每当 $xRy$ ，就有 $yRx$ ，则称集合 $X$ 上关系 $R$ 是对称的。
  $\forall x \forall y[(x,y)\in R \rightarrow (y,x)\in R]$
• 反对称性(antisymmetric)
  定义：
  设 $R$ 为定义在集合 $X$ 上的二元关系，如果对于每个 $x,y\in X$ ，每当 $xRy$ 和 $yRx$ 必有 $x=y$ ，则称 $R$ 在 $X$ 上是反对称的。
  $\forall x \forall y[(x,y)\in R \wedge (y,x) \rightarrow x=y ]$
• 传递性(transitive)
  定义：
  设 $R$ 为定义在集合 $X$ 上的二元关系，如果对于每个 $x,y,z\in X$ ，每当 $xRy,yRz$ ，就有 $xRz$ ，则称集合 $X$ 上关系 $R$ 是传递的。
  $\forall x \forall y \forall z [(x,y)\in R \wedge (y,z)\in R \rightarrow (x,z)\in R]$

3.3.3.关系的组成与复合

• 关系的组成(combination)
  关系的本质是集合，故而集合的一系列运算，关系也都可以进行。
  设 $R_1,R_2$为两个关系，譬如，可进行下列运算。
  $R_1 \cup R_2$
  $R_1 \cap R_2$
  $R_1 - R_2$ 等等。

• 关系的复合(composition)
  设 $R$ 为 $X$ 到 $Y$ 的关系， $S$ 为从 $Y$ 到 $Z$ 的关系，则 $S \circ R$ 称为 $S$ 和 $R$ 的复合关系，表示为 $X$到 $Z$的关系。注意，此处关系的先后顺序，与函数的复合不一样。

• 关系自身的复合
  关系 $R$ 本身所组成的复合关系可以写成： $R \circ R,R \circ R \circ R,\cdots,\overbrace{R \circ R \circ \cdots \circ R}^n$ ，分别记作 $R^{2},R^{3},\cdots,R^{n}$ ，一般地， $R^{n-1}\circ R=R^{n}$ 。

• 一个重要定理
  $A$上的关系 $R$具有传递性，当且仅当 $R^n\subseteq R$,
  此定理可以用数学归纳法证明。

3.2.4.关系的表示

• 用矩阵表示关系
  $m_{ij}=\begin{cases}1,if(a_i,b_j)\in R\\0,if(a_i,b_j)\notin R\end{cases}$
  如果关系具有自反性，那么主对角线上的元素都为1;
  
  下面是对称性和反对称性的特征矩阵
  

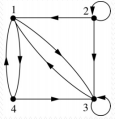
• 用有向图表示关系
  
  上图表示关系 ${(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,3),(4,1),(4,3)}$

• 关系的性质与图的特征
  自反性：所有顶点都有自环(loop)
  反自反性: 图中没有自环出现。
  对称性：图中没有单向边。
  反对称性：图中无双向边
  传递性：难以直接观察得出，可以对将所有的边两两组合判断。

3.3.闭包(Closure)

3.3.1.闭包的定义

定义 3 - 8.1
设 $R$ 是 $X$ 上的二元关系，如果有另一个关系 $R'$ 满足：

• $R'$ 是自反的（对称的，可传递的）。
• $R' \supseteq R$ 。
• 对于任何自反的（对称的，可传递的）关系 $R''$ ，如果有 $R'' \supseteq R$ ，就有 $R'' \supseteq R'$ 。则称关系 $R'$ 为 $R$ 的自反（对称、传递）闭包。记作 $r(R)$ （ $s(R)$ ， $t(R)$ ）。

在这个定义里，除了关系 $R$,和闭包 $R^{'}$,还引入了关系 $R^{''}$,就是为了强调从关系R转换为满足某种性质的关系时，需要尽可能添加尽可能少的序偶。这就保证闭包的产生是唯一。

（这里的三个字母分别是 reverse、symmetric 和 transmit 的首字母）

3.4.等价(Equivalence)

3.4.1.等价关系(Equivalence Relations)

• 定义：如果一个关系是自反的、对称的、传递的，那么这个关系就称为等价关系。

• 元素的等价
  如果两个元素由于等价关系而相关联，则称它们是等价的，记为 $a$~ $b$。

• 模m同余关系
  定义关系 $R=\{(a,b)|a\equiv b(mod \,\ m)\}$，模m同余关系就是一种等价关系。

3.4.2.等价类

• 定义：
  设 $R$ 为定义在集合 $A$ 上的等价关系，对任何 $a \in A$ ，集合 $[a]_R = \{ x \vert x \in A , aRx \}$ 称为元素 $a$ 形成的 $R$ 等价类。

以模m同余关系为例，它定义在整数集合 $Z$上，模m同余关系的等价类叫做模m同余类。具体地，
$[0]_m =\{……,-2m，-m,0,m,2m,……,\}$，
$[1]_m =\{……,-2m+1，-m+1,1,m+1,2m+1,……,\}$
……
$[m-1]_m=\{……,-m-1,-1,m-1,2m-1\}$

注： $Z_m=\{[0],[1],[2],……,[m-1]\}$称为模m剩余类的集合。

3.4.3.划分

• 三个等价命题
  (i) $aRb$
  (ii) $[a]=[b]$
  (iii) $[a]\cap [b]=\varnothing$
  这三个命题是等价的，这里不予证明。

• 划分的定义
  令 $S$ 为给定非空集合， $A=\{A_1,A_2,\cdots,A_m\}$ ，其中 $A_i\subseteq S,A_i\ne\varnothing(i=1,2,\cdots,m)$ 且 $\bigcup\limits_{i=1}^mA_i=S$ ，集合 $A$ 称作集合 $S$ 的覆盖。如果除以上条件外，还另有 $A_i\cap A_j=\varnothing(i\ne j)$ ，则称 $A$ 是 $S$ 的划分。
  由定义知，所谓划分就是一个集合，它里面的元素是由等价关系确定的等价类。
  自然，这些元素的交集必为空。

  

• 商集
  集合 $A$ 上的等价关系 $R$ ，其等价类集合 $\{ [a]_R \vert a \in A \}$ 称作 $A$ 关于 $R$ 的商集，记作 $A/R$ 。

• 划分与等价关系的联系
  (i) 集合 $A$ 上的等价关系 $R$ ，决定了 $A$ 的一个划分，该划分就是商集 $A/R$ 。
  (ii)集合 $A$ 的一个划分确定 $A$ 的元素间的一个等价关系。

3.5.偏序(Partial order)

3.5.1.偏序关系与偏序集

• 定义
  设 $A$ 是一个集合，如果 $A$ 上的一个关系 $R$ ，满足自反性，反对称性和传递性，则称 $R$ 是 $A$ 上的一个偏序(关系)，并把R记为“ $\preccurlyeq$ ”。
  序偶 $(A,\preccurlyeq )$ 称作偏序集(poset)。
  集合A中的元素称之为偏序集的元素。

• 可比较性
  偏序集中的元素a,b是可比较的，如果%a≤b $或者$b≤a$ 。如果a,b是偏序集中的元素，但是即不存在 $a≤b$，也不存在 $b≤a$，则称a,b是不可比较的。
  可比较性反映在关系图中就是单向边的存在与否。

• 全序集、线序集
  如果 $(S,R)$是偏序集，并且S中每对元素都是可比较的，则称S为全序集或线序集，R为全序或线序。一个全序集，也称之为链。

3.5.2.字典序（Lexicographic Order）

• 定义：
  给定两个偏序集 $(A_1,≤_1)$和 $(A_2,≤_2)$， $A_1\times A_2$上的字典序定义为, $(a_1,a_2)<(b_1,b_2)$，如果， $(i)a_1<b_1$,或者如果， $(ii)(a_1=b_1,and\,\ a_2<b_2 )$,注意这里是严格小于。

3.5.3.哈斯图

• 盖住
  在偏序集合 $\langle A,\preccurlyeq \rangle$ 中，如果 $x,y \in A,x \preccurlyeq y,x \ne y$ 且没有其他元素 $z$ 满足 $x \preccurlyeq z,z\preccurlyeq y$ ，则称元素 $y$ 盖住元素 $x$ 。并且记集合
  $\{ \langle x,y \rangle \vert x,y \in A;y盖住x\}$
  为 $\text{COV }A$ 。

对于给定偏序集 $\langle A,\preccurlyeq\rangle$ ，它的盖住关系是唯一的，所以可用盖住的性质画出偏序集合图，或称哈斯图，其作图规则为：

• 作图规则

1. 用小圆圈代表元素。
2. 如果 $x\preccurlyeq y$ 且 $x\ne y$ ，则将代表 $y$ 的小圆圈画在代表 $x$ 的小圆圈上方。
3. 如果 $\langle x,y \rangle\in \text{COV }A$ ，则在 $x$ 与 $y$ 之间用直线连接。

也就是，将一张普通的关系图，（i）去掉自环，（ii）去掉可由传递性得出边，（iii）再将元素从下往上的放置。
如下图：

3.5.4.偏序集中的元素

• 极大元、极小元（Greatest and Least Elements）
  定义：
  设 $\langle A,\preccurlyeq \rangle$ 是一个偏序集合，且 $B$ 是 $A$ 的子集，对于 $B$ 中的一个元素 $b$ ，如果 $B$ 中没有任何元素 $x$ 满足 $b \ne x$ 且 $b \preccurlyeq x$ ，则称 $b$ 为 $B$ 的极大元。同理，对于 $b \in B$ ，如果 $B$ 中没有任何元素 $x$ ，满足 $b \ne x$ 且 $x \preccurlyeq b$ ，则称 $b$ 为 $B$ 的极小元。

• 对于有穷集合，极大元、极小元必存在，但不一定唯一。

• 最大元、最小元（Maximal and Minimal Elements）
  定义：
  令 $\langle A,\preccurlyeq \rangle$ 是一个偏序集，且 $B$ 是 $A$ 的子集，若有某个元素 $b \in B$ ，对于 $B$ 中每一个元素 $x$ 有 $x \preccurlyeq b$ ，则称 $b$ 为 $\langle B,\preccurlyeq \rangle$ 的最大元。同理，若有某个元素 $b \in B$ ，对每一个 $x \in B$ 有 $b \preccurlyeq x$ ，则称 $b$ 为 $\langle B,\preccurlyeq \rangle$ 的最小元。

• 最大元、最小元不一定存在，但存在就必唯一；并且，最小元一定是极小元，最大元一定是极大元.

• 上界、下界
  定义：
  设 $\langle A,\preccurlyeq \rangle$ 为一偏序集，对于 $B\subseteq A$ ，如有 $a\in A$ ，且对 $B$ 的任意元素 $x$ ，都满足 $x\preccurlyeq a$ ，则称 $a$ 为子集 $B$ 的上界。同样地，对于 $B$ 的任意元素 $x$ ，都满足 $a\preccurlyeq x$ ，则称 $a$ 为 $B$ 的下界。
  这是借助子集来定义的。

• 最小上界、最大下界
  定义：
  设 $\langle A,\preccurlyeq \rangle$ 为偏序集且 $B\subseteq A$ 为一子集， $a$ 为 $B$ 的任一上界，若对 $B$ 的所有上界 $y$ 均有 $a\preccurlyeq y$ ，则称 $a$ 为 $B$ 的最小上界（上确界），记作 $\text{LUB }B$ 。同样，若 $b$ 为 $B$ 的任一下界，若对 $B$ 的所有下界 $z$ ，均有 $z\preccurlyeq b$ ，则称 $b$ 为 $B$ 的最大下界（下确界），记作 $\text{GLB }B$ 。