MIT_Linear_Algebra_lec15：投影到子空间

Lecture 15: Projection onto Subspaces

MIT 公开课：Gilbert Strang《线性代数》课程笔记（汇总

---

投影

为什么投影

当 $Ax = b$ 无解时，而 $Ax = p$ 有解
（其中p是b向A的列空间投影得到的向量）

• 解释：当b不在A的列空间中，那么我们就把b投影到A的列空间中

投影过程

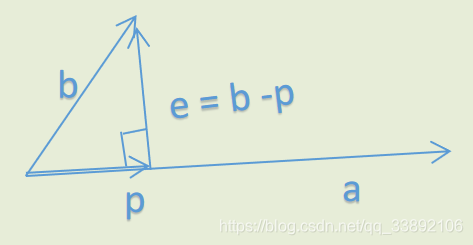
一维情况

$b$ 投影到 $a$ 上， 在 $a$ 上的分量就是 $p$

1. $p$ 与 $a$ 同方向。
   $p = xa,x ∈ R$

2. 注意这里有一个直角。根据直角可以得到 $e$与 $a$正交，由此可以得到x。

   $a^T(b -xa ) = 0$

   $∴x = a^Tb/ a^Ta，p = a(a^Tb/ a^Ta)$

   $p = Pb = (aa^T/a^Ta)b$

投影矩阵

$P$ 是投影矩阵，作用于 $b$ 上，让 $Pb$ 成为 $a$ 方向的投影, 即 $xa = f(b) = Pb$。

性质

$P^T = P, P^2 = P（p再在a上的投影还是自己）$

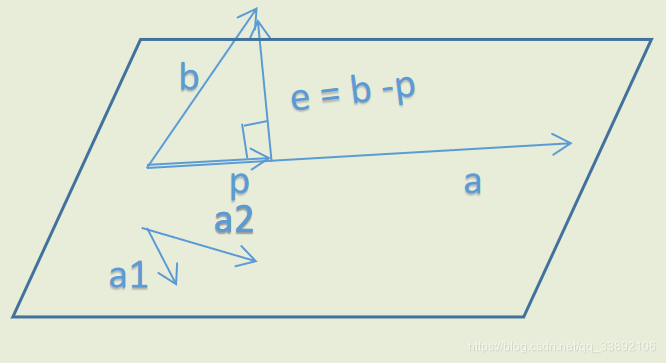
二维情况

$A$ 的列空间是 $[a_1, a_2]$

1. $p = x_1a1 + x_2a2 = Ax$，p是在A的列空间中的。

2. $p与a_1,a_2正交$

   $a_1^T(b - Ax) = 0, a_2^T (b - Ax) = 0$
   $\left[ \begin{matrix} a_1^T \\ a_2^T \\ \end{matrix} \right] (b - Ax) = \left[ \begin{matrix} 0 \\ 0 \\ \end{matrix} \right]$

3. $A^T(b - Ax) = 0$

   $∴ x = (A^TA)^-1A^Tb, P = A(A^TA)^-1A^T$

   注意： $A^TA$不一定有逆矩阵， $A$不一定有逆矩阵;
   r( $A^TA$) = r( $A$),且零空间一致

性质 同上